Chủ đề bài momen lực: Bài viết này cung cấp kiến thức toàn diện về momen lực, bao gồm định nghĩa, công thức và ứng dụng thực tế. Hãy khám phá những nguyên lý quan trọng và thực hành qua các bài tập chi tiết để nắm vững cách áp dụng momen lực trong nhiều lĩnh vực khác nhau.
Mục lục
Momen Lực: Kiến Thức Cơ Bản và Bài Tập Vận Dụng
Momen lực là một khái niệm quan trọng trong vật lý, đặc biệt trong lĩnh vực cơ học. Nó liên quan đến lực và khoảng cách từ trục quay đến điểm đặt lực. Dưới đây là tổng hợp các kiến thức cơ bản và bài tập vận dụng liên quan đến momen lực.
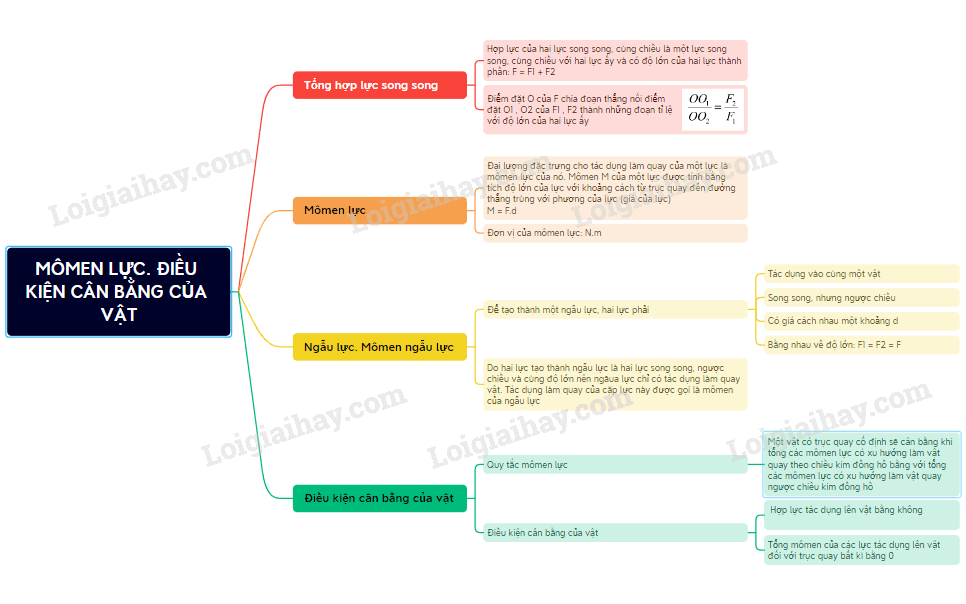
1. Khái Niệm Momen Lực
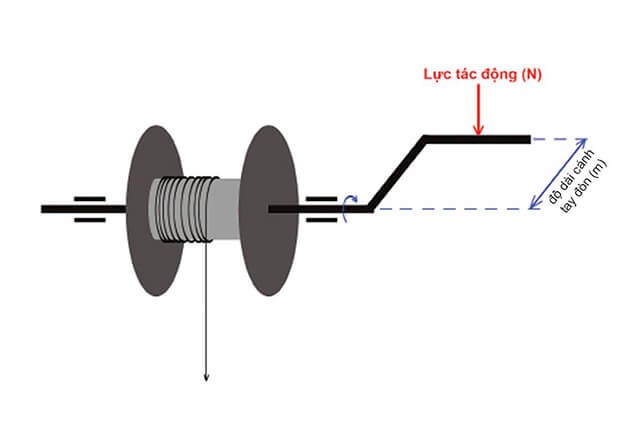
Momen lực (M) được tính bằng tích của lực tác dụng (F) và khoảng cách từ trục quay đến điểm đặt lực (d), công thức:
M = F × d
Trong đó:
- F: Độ lớn của lực tác dụng (đơn vị: Newton, N)
- d: Khoảng cách từ trục quay đến giá của lực, gọi là cánh tay đòn của lực (đơn vị: mét, m)
- M: Momen lực (đơn vị: Newton-mét, N.m)
2. Quy Tắc Momen Lực và Điều Kiện Cân Bằng
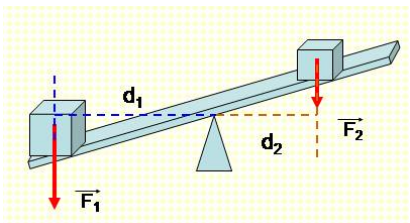
Để một vật rắn có thể cân bằng khi chịu tác động của các lực, tổng các momen lực làm vật quay theo chiều kim đồng hồ phải bằng tổng các momen lực làm vật quay ngược chiều kim đồng hồ:
Σ Mcw = Σ Mccw
Quy tắc này áp dụng trong nhiều tình huống thực tế như cân bằng của các vật thể trên cân, lực căng của dây cáp, và các hệ thống cơ khí.
3. Các Bài Tập Về Momen Lực
- Bài tập 1: Một thanh chắn dài 7,5 m, khối lượng 25 kg, trọng tâm cách đầu A 1,2 m. Tính lực cần tác dụng lên đầu B để thanh cân bằng nằm ngang. (Đáp án: 12,5 N)
- Bài tập 2: Một lực F = 100 N tác dụng lên cánh tay đòn dài 0,5 m. Tính momen lực tạo ra. (Đáp án: 50 N.m)
- Bài tập 3: Tính lực căng của sợi dây giữ một thanh gỗ dài 1,8 m, nặng 30 kg khi treo nghiêng với trần nhà một góc 45° và trọng tâm cách điểm gắn dây 60 cm. (Đáp án: 200 N)
4. Ứng Dụng Của Momen Lực Trong Thực Tế
Momen lực có ứng dụng rộng rãi trong nhiều lĩnh vực:
- Kỹ thuật cơ khí: Sử dụng trong thiết kế máy móc để đảm bảo an toàn và hiệu quả.
- Xây dựng: Ứng dụng trong tính toán thiết kế các cấu trúc chịu lực như cầu, nhà cao tầng.
- Thể thao: Giúp cải thiện kỹ năng trong các môn như golf, cricket.
- Phương tiện giao thông: Giúp cân bằng và điều khiển ô tô, máy bay.
5. Một Số Bài Tập Khác
Dưới đây là một số bài tập khác giúp bạn luyện tập và nâng cao kiến thức về momen lực:
| Bài Tập | Mô Tả | Đáp Án |
|---|---|---|
| Bài tập 4 | Lực 80 N tác dụng lên cánh tay đòn dài 0,5 m. Tính momen lực. | 40 N.m |
| Bài tập 5 | Momen lực 45 N.m tác dụng lên cánh tay đòn dài 0,9 m. Tính lực tác dụng. | 50 N |

.png)
1. Khái niệm Momen Lực
Momen lực (còn gọi là moment hoặc torque) là đại lượng vật lý mô tả khả năng gây quay của một lực quanh một trục cố định. Momen lực không chỉ phụ thuộc vào độ lớn của lực mà còn vào vị trí điểm đặt lực so với trục quay.
Cụ thể, momen lực được xác định bằng tích của độ lớn lực (F) và khoảng cách vuông góc từ trục quay đến đường thẳng chứa lực (d). Công thức tính momen lực được biểu diễn như sau:
\[ M = F \times d \]
Trong đó:
- M: Momen lực (đơn vị: Nm - Newton mét)
- F: Lực tác dụng (đơn vị: N - Newton)
- d: Khoảng cách vuông góc từ trục quay đến đường thẳng chứa lực (đơn vị: m - mét)
Momen lực có thể dương hoặc âm tùy thuộc vào hướng quay của lực quanh trục cố định. Nếu lực làm cho vật quay theo chiều kim đồng hồ, momen lực được coi là âm, ngược lại, nếu quay ngược chiều kim đồng hồ, momen lực được coi là dương.
Khái niệm momen lực đóng vai trò quan trọng trong nhiều lĩnh vực như cơ khí, xây dựng, và điện tử, giúp chúng ta hiểu và thiết kế các hệ thống hoạt động một cách hiệu quả và an toàn.
2. Công thức tính Momen Lực
Công thức tính momen lực rất quan trọng trong việc xác định hiệu quả của lực tác dụng lên một vật thể. Để tính toán momen lực, chúng ta sử dụng công thức sau:
\[ M = F \times d \times \sin(\theta) \]
Trong đó:
- M: Momen lực (đơn vị: Nm - Newton mét)
- F: Độ lớn của lực tác dụng (đơn vị: N - Newton)
- d: Khoảng cách vuông góc từ trục quay đến điểm đặt lực (đơn vị: m - mét)
- \(\theta\): Góc giữa đường thẳng chứa lực và đường vuông góc từ trục quay đến điểm đặt lực
Để hiểu rõ hơn về công thức này, chúng ta hãy xem xét từng yếu tố:
- Độ lớn lực (F): Lực càng lớn, momen lực càng mạnh, điều này làm tăng khả năng gây quay của vật.
- Khoảng cách vuông góc (d): Khoảng cách này càng dài, momen lực càng lớn. Đó là lý do tại sao tay cầm dài hơn giúp bạn mở nắp chai dễ dàng hơn.
- Góc \(\theta\): Khi lực tác dụng theo phương vuông góc với khoảng cách d, tức là \(\theta = 90^\circ\), thì momen lực đạt giá trị lớn nhất. Khi \(\theta\) giảm, momen lực cũng giảm theo.
Trong các trường hợp thực tế, công thức có thể đơn giản hơn nếu lực tác dụng vuông góc với đoạn thẳng nối từ trục quay đến điểm đặt lực, khi đó công thức trở thành:
\[ M = F \times d \]
Việc áp dụng công thức momen lực một cách chính xác giúp đảm bảo tính ổn định và an toàn của các hệ thống cơ học và công trình kỹ thuật.

3. Các ứng dụng của Momen Lực trong thực tế
Momen lực là một khái niệm quan trọng và có nhiều ứng dụng trong thực tế, từ kỹ thuật cơ khí, xây dựng đến đời sống hàng ngày. Dưới đây là một số ứng dụng tiêu biểu của momen lực:
3.1 Ứng dụng trong kỹ thuật cơ khí
- Động cơ và máy móc: Momen lực đóng vai trò quan trọng trong việc thiết kế và vận hành các loại động cơ, máy móc. Việc xác định chính xác momen lực giúp tối ưu hóa hiệu suất và độ bền của máy móc.
- Công cụ cầm tay: Các công cụ như cờ lê, tua vít được thiết kế để tăng momen lực, giúp dễ dàng vặn các ốc vít hoặc bu lông cứng đầu.
3.2 Ứng dụng trong xây dựng
- Thiết kế cầu và kết cấu: Momen lực được sử dụng để tính toán độ bền và ổn định của cầu, tòa nhà và các công trình lớn khác. Điều này đảm bảo các cấu trúc chịu được lực tác động mà không bị sụp đổ.
- Cân bằng cấu trúc: Trong xây dựng, momen lực được áp dụng để đảm bảo sự cân bằng và an toàn của các phần tử cấu trúc khi chịu tải trọng không đối xứng.
3.3 Ứng dụng trong thể thao
- Các môn thể thao như cử tạ, đạp xe: Vận động viên sử dụng momen lực để tối ưu hóa lực phát ra, tăng cường hiệu suất và thành tích. Ví dụ, việc sử dụng momen lực trong động tác đạp xe giúp chuyển hóa sức mạnh cơ bắp thành lực quay bánh xe.
- Kỹ thuật ném, đánh: Trong bóng chày, bóng rổ, hoặc golf, người chơi cần điều chỉnh momen lực để tối ưu hóa quỹ đạo và tốc độ của quả bóng.
3.4 Ứng dụng trong thiết bị gia dụng
- Cửa tự động: Momen lực được tính toán để đảm bảo cửa tự động mở và đóng một cách trơn tru và an toàn, phù hợp với các tiêu chuẩn về an toàn.
- Máy giặt: Trong máy giặt, momen lực được sử dụng để quay lồng giặt, đảm bảo quá trình giặt hiệu quả và không gây hư hỏng cho quần áo.
3.5 Ứng dụng trong robot học
- Thiết kế cánh tay robot: Momen lực là yếu tố chính trong việc thiết kế và điều khiển cánh tay robot, giúp chúng có thể nâng, di chuyển các vật nặng với độ chính xác cao.
- Hệ thống lái tự động: Trong các xe tự lái, momen lực được tính toán để điều chỉnh góc lái, đảm bảo xe di chuyển an toàn và ổn định trên đường.
Các ứng dụng của momen lực không chỉ giới hạn trong những ví dụ trên mà còn mở rộng đến nhiều lĩnh vực khác, đóng vai trò quan trọng trong việc cải thiện chất lượng cuộc sống và phát triển công nghệ.

XEM THÊM:
4. Bài tập Momen Lực
Để hiểu rõ hơn về momen lực và cách áp dụng nó trong thực tế, chúng ta sẽ cùng nhau giải quyết một số bài tập từ cơ bản đến nâng cao. Các bài tập này sẽ giúp bạn củng cố kiến thức và nâng cao kỹ năng giải quyết vấn đề liên quan đến momen lực.
4.1 Bài tập lý thuyết
- Bài tập 1: Một lực có độ lớn 10 N tác dụng vuông góc lên một thanh có chiều dài 2 m từ trục quay. Tính momen lực tác dụng lên thanh.
- Bài tập 2: Giả sử một lực tác dụng lên một cánh cửa với khoảng cách từ bản lề đến điểm tác dụng lực là 0,8 m và tạo một góc 60 độ so với mặt phẳng của cánh cửa. Nếu độ lớn lực là 15 N, tính momen lực tác dụng lên cánh cửa.
4.2 Bài tập thực hành
- Bài tập 3: Hãy sử dụng một cờ lê để vặn một bu lông, biết rằng lực bạn tác dụng là 50 N và chiều dài tay cầm cờ lê là 0,3 m. Tính momen lực bạn tạo ra và nhận xét về việc tăng chiều dài tay cầm cờ lê sẽ ảnh hưởng như thế nào đến momen lực.
- Bài tập 4: Tìm hiểu cách momen lực được sử dụng trong thiết kế cầu và viết một báo cáo ngắn về cách tính toán momen lực giúp đảm bảo tính ổn định của cầu khi chịu tải trọng lớn.
4.3 Bài tập ứng dụng
- Bài tập 5: Một cần cẩu xây dựng có cánh tay dài 5 m và nâng một vật nặng 2000 kg tại đầu cần. Tính momen lực mà cần cẩu phải chịu. (Giả sử gia tốc trọng trường \( g = 9,8 \, \text{m/s}^2 \)).
- Bài tập 6: Một người công nhân cần sử dụng một thanh đòn để nâng một khối đá nặng 500 kg. Nếu điểm tựa cách khối đá 1 m và người công nhân tác dụng một lực tại đầu thanh đòn với khoảng cách 3 m từ điểm tựa, tính lực tối thiểu mà người công nhân cần tác dụng để nâng được khối đá.
Các bài tập trên không chỉ giúp bạn nắm vững lý thuyết mà còn có thể áp dụng kiến thức momen lực vào thực tế, từ đó nâng cao khả năng tư duy và kỹ năng giải quyết vấn đề trong cuộc sống hàng ngày.

5. Tổng kết về Momen Lực
Momen lực là một khái niệm vật lý cốt lõi, với ứng dụng rộng rãi trong nhiều lĩnh vực từ cơ khí, xây dựng đến đời sống hàng ngày. Hiểu rõ về momen lực không chỉ giúp chúng ta tối ưu hóa các thiết kế cơ học mà còn đảm bảo an toàn và hiệu suất trong quá trình sử dụng các công cụ, máy móc và công trình kỹ thuật.
Từ những bài học lý thuyết cơ bản về momen lực, chúng ta đã thấy được tầm quan trọng của việc tính toán chính xác để áp dụng trong thực tế. Việc hiểu và áp dụng đúng momen lực giúp tăng cường khả năng kiểm soát các hệ thống, giảm thiểu rủi ro và tối đa hóa hiệu suất làm việc.
Trong thiết kế công trình, sự cân bằng momen lực là yếu tố then chốt để đảm bảo sự ổn định và bền vững của cấu trúc. Trong kỹ thuật cơ khí, việc tính toán momen lực cho phép thiết kế các máy móc và thiết bị với hiệu suất cao và an toàn tối đa.
Momen lực cũng là một phần không thể thiếu trong các lĩnh vực như thể thao và đời sống hàng ngày, nơi mà hiểu biết về nguyên lý này có thể cải thiện kỹ năng và hiệu quả công việc. Từ việc vặn chặt một con ốc đến việc thiết kế một cánh tay robot, momen lực luôn hiện diện và có vai trò quan trọng.
Tổng kết lại, momen lực không chỉ là một khái niệm lý thuyết mà còn là một công cụ thực tế, giúp con người tối ưu hóa mọi hoạt động trong cuộc sống. Việc nắm vững kiến thức này sẽ mở ra nhiều cơ hội và khả năng mới, góp phần vào sự phát triển bền vững và hiện đại hóa trong mọi lĩnh vực.