Bài 14: Momen Lực - Điều Kiện Cân Bằng Của Vật: Hướng Dẫn Chi Tiết và Ứng Dụng Thực Tế

Bài 14 trong chương trình Vật lý lớp 10 thuộc sách giáo khoa "Chân trời sáng tạo" tập trung vào khái niệm momen lực và điều kiện cân bằng của vật. Đây là những kiến thức cơ bản nhưng rất quan trọng, giúp học sinh hiểu rõ hơn về cách các lực tác dụng lên vật thể và điều kiện để vật thể đó ở trạng thái cân bằng.

1. Khái niệm về Momen Lực

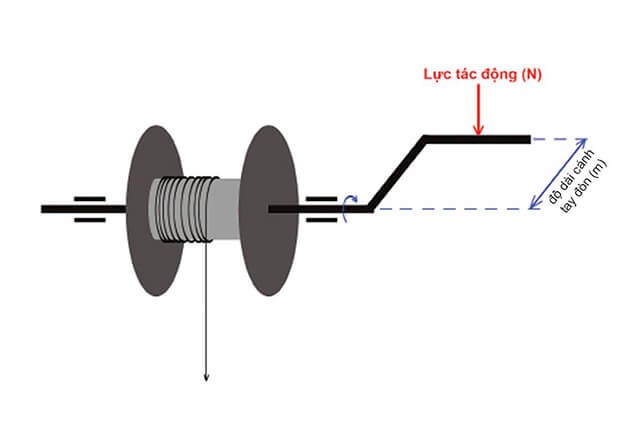
Momen lực là đại lượng đặc trưng cho khả năng làm quay của một lực đối với một trục quay cố định. Công thức tính momen lực được biểu diễn như sau:

\( M = F \times d \)

Trong đó:

• M: Momen lực (đơn vị: Newton mét, ký hiệu là Nm)
• F: Lực tác dụng lên vật (đơn vị: Newton, ký hiệu là N)
• d: Khoảng cách từ trục quay đến đường tác dụng của lực (đơn vị: mét)

2. Điều Kiện Cân Bằng Của Vật

Một vật ở trạng thái cân bằng khi và chỉ khi tổng các lực tác dụng lên vật và tổng các momen lực đối với một trục quay bất kỳ đều bằng không. Các điều kiện cụ thể bao gồm:

1. Điều kiện cân bằng tịnh tiến: Tổng hợp các lực tác dụng lên vật phải bằng 0.

   \( \sum \vec{F} = 0 \)

2. Điều kiện cân bằng quay: Tổng hợp các momen lực tác dụng lên vật đối với một điểm bất kỳ phải bằng 0.

   \( \sum M = 0 \)

3. Ví Dụ Minh Họa

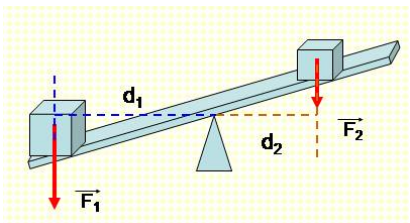
Giả sử có hai vật có khối lượng lần lượt là \( m_1 = 5 \, kg \) và \( m_2 = 2 \, kg \) đặt trên một thanh thẳng nằm ngang, thanh này không có khối lượng đáng kể và nằm cân bằng trên một cạnh nêm. Bài toán yêu cầu tính khoảng cách từ vật đến điểm tựa O và lực do cạnh nêm tác dụng lên điểm tựa.

Kết quả tính toán cho thấy:

\( d_2 = \frac{m_1}{m_2} \times d_1 \)

và lực do cạnh nêm tác dụng lên điểm tựa O là:

\( F = P_1 + P_2 = m_1 \times g + m_2 \times g \)

4. Ứng Dụng Thực Tiễn

Momen lực và điều kiện cân bằng có ứng dụng rộng rãi trong đời sống và kỹ thuật. Một ví dụ điển hình là việc sử dụng momen lực trong các dụng cụ như cờ lê, kéo, và các thiết bị nâng hạ. Hiểu và áp dụng đúng momen lực giúp đảm bảo an toàn và hiệu quả trong công việc.

5. Bài Tập Trắc Nghiệm

Để củng cố kiến thức, học sinh có thể làm các bài tập trắc nghiệm với các câu hỏi liên quan đến momen lực và điều kiện cân bằng của vật. Một số câu hỏi có thể bao gồm:

• Momen lực là gì và được đo bằng đơn vị nào?
• Điều kiện để một vật ở trạng thái cân bằng tịnh tiến là gì?
• Khi nào một vật chịu tác dụng của momen lực thì nó sẽ quay quanh trục nào?

Các bài tập này giúp học sinh nắm vững lý thuyết và vận dụng vào thực tiễn một cách hiệu quả.

Kết Luận

Chương trình học bài 14 về momen lực và điều kiện cân bằng của vật mang lại cho học sinh những kiến thức cơ bản nhưng quan trọng. Hiểu rõ những khái niệm này giúp học sinh ứng dụng chúng vào các tình huống thực tế, nâng cao kỹ năng giải quyết vấn đề và nhận thức khoa học.

Momen lực là một khái niệm quan trọng trong cơ học, dùng để mô tả hiệu quả của lực trong việc làm quay một vật quanh một trục cố định. Hiểu rõ momen lực giúp chúng ta phân tích các tình huống cơ học liên quan đến cân bằng và chuyển động quay.

• Định nghĩa: Momen lực của một lực đối với một trục quay được định nghĩa là tích của lực và khoảng cách vuông góc từ trục quay đến đường tác dụng của lực. Công thức tổng quát được biểu diễn dưới dạng:

  \( M = F \times d \)

  Trong đó:
  • \( M \): Momen lực (đơn vị: Newton mét - Nm)
  • \( F \): Lực tác dụng lên vật (đơn vị: Newton - N)
  • \( d \): Khoảng cách vuông góc từ trục quay đến đường tác dụng của lực (đơn vị: mét - m)
• Đơn vị đo: Đơn vị đo của momen lực là Newton mét (Nm), một đơn vị kết hợp giữa lực và khoảng cách.
• Quy tắc dấu: Momen lực có thể là dương hoặc âm tùy thuộc vào chiều của lực quay quanh trục:
  • Momen dương nếu lực tạo ra chuyển động quay theo chiều kim đồng hồ.
  • Momen âm nếu lực tạo ra chuyển động quay ngược chiều kim đồng hồ.
• Ứng dụng: Momen lực có vai trò quan trọng trong việc xác định trạng thái cân bằng của vật. Ví dụ, trong các bài toán về cân bằng lực trên đòn bẩy, momen lực là yếu tố chính để tính toán vị trí và cường độ của lực cần thiết để đạt được cân bằng.

Momen lực không chỉ là một khái niệm lý thuyết mà còn có ứng dụng thực tiễn rộng rãi trong đời sống hàng ngày và các ngành công nghiệp, như cơ khí, xây dựng, và thiết kế máy móc.

Điều kiện cân bằng của một vật là các tiêu chí mà khi thỏa mãn, vật sẽ ở trạng thái cân bằng, tức là không có chuyển động tịnh tiến hay quay. Để đạt được trạng thái này, cần thỏa mãn hai điều kiện cơ bản: cân bằng tịnh tiến và cân bằng quay.

• 1. Điều kiện cân bằng tịnh tiến:

  Điều kiện này yêu cầu tổng hợp của tất cả các lực tác dụng lên vật phải bằng không. Nói cách khác, không có lực tổng hợp nào tác động làm thay đổi trạng thái chuyển động của vật.

  \( \sum \vec{F} = 0 \)

  Trong đó:

  • \( \vec{F} \): là các vector lực tác dụng lên vật
• 2. Điều kiện cân bằng quay:

  Điều kiện này yêu cầu tổng hợp của tất cả các momen lực tác dụng lên vật đối với một trục quay phải bằng không. Điều này có nghĩa là không có momen tổng hợp nào làm cho vật quay quanh trục.

  \( \sum M = 0 \)

  Trong đó:

  • \( M \): là các momen lực tác dụng lên vật quanh trục quay

Để kiểm tra điều kiện cân bằng của một vật trong thực tế, chúng ta cần tính toán và đảm bảo rằng cả hai điều kiện trên đều được thỏa mãn. Nếu chỉ một trong hai điều kiện bị phá vỡ, vật sẽ mất cân bằng và có thể xảy ra chuyển động tịnh tiến hoặc quay.

Điều kiện cân bằng không chỉ áp dụng trong lý thuyết mà còn có ứng dụng thực tiễn rộng rãi, ví dụ trong thiết kế cầu, xây dựng nhà cửa, và lắp đặt các thiết bị cơ khí, nơi mà sự ổn định và an toàn luôn được đặt lên hàng đầu.

Cân bằng của vật là trạng thái mà vật không bị dịch chuyển tịnh tiến hoặc quay. Để duy trì cân bằng, có nhiều yếu tố khác nhau ảnh hưởng đến trạng thái này. Dưới đây là các yếu tố chính cần phân tích khi đánh giá sự cân bằng của vật.

• 1. Vị trí đặt lực:

  Vị trí mà lực tác dụng lên vật có ảnh hưởng lớn đến sự cân bằng của vật. Nếu lực được đặt tại một vị trí không hợp lý, nó có thể tạo ra một momen lớn làm cho vật mất cân bằng. Khi lực được đặt càng xa trục quay, momen lực càng lớn, làm tăng khả năng vật bị quay.

• 2. Trục quay và khoảng cách từ trục quay đến điểm tác dụng lực:

  Khoảng cách từ trục quay đến điểm mà lực tác dụng (gọi là cánh tay đòn) quyết định mức độ ảnh hưởng của lực đó đến cân bằng của vật. Một cánh tay đòn dài sẽ tạo ra momen lực lớn hơn, làm tăng khả năng mất cân bằng nếu không có lực đối trọng phù hợp.

• 3. Trọng lực và vị trí trọng tâm:

  Trọng lực tác dụng lên vật qua trọng tâm, do đó, vị trí của trọng tâm rất quan trọng. Nếu trọng tâm nằm dưới trục quay hoặc trong vùng được các lực cân bằng chi phối, vật sẽ dễ dàng đạt được trạng thái cân bằng. Tuy nhiên, nếu trọng tâm nằm trên hoặc ngoài vùng này, nguy cơ mất cân bằng sẽ cao hơn.

• 4. Các lực tác dụng đồng thời:

  Nếu có nhiều lực tác dụng lên vật đồng thời, ta cần xem xét tổng hợp các lực và momen lực để đánh giá cân bằng. Các lực này có thể tác động theo các phương khác nhau, tạo ra các momen khác nhau, và chúng phải được tính toán cẩn thận để đảm bảo rằng tổng các momen bằng không, giúp vật giữ trạng thái cân bằng.

• 5. Ứng dụng thực tế:

  Trong thực tế, các yếu tố này thường được tính toán kỹ lưỡng khi thiết kế các công trình xây dựng, cầu đường, và thiết bị cơ khí. Đảm bảo sự cân bằng giúp tăng độ an toàn và hiệu quả của các cấu trúc và máy móc.

Việc hiểu và phân tích đúng các yếu tố ảnh hưởng đến cân bằng của vật là nền tảng để giải quyết các bài toán cơ học phức tạp, cũng như ứng dụng trong thiết kế và xây dựng.

Trong phần này, chúng ta sẽ đi sâu vào các ví dụ minh họa cụ thể về momen lực và điều kiện cân bằng của vật. Những ví dụ này không chỉ giúp củng cố kiến thức lý thuyết mà còn giúp chúng ta hiểu rõ hơn về ứng dụng của momen lực trong thực tế.

1. Ví dụ về hệ vật cân bằng trên thanh ngang

Giả sử chúng ta có một thanh ngang đồng chất, được đặt trên hai điểm tựa O và A. Trên thanh có một vật nặng đặt tại điểm B cách điểm O một khoảng cách d₁ và điểm A một khoảng cách d₂.

• Thanh ngang có khối lượng m, tác dụng một lực trọng trường P = mg tại trọng tâm của thanh.
• Vật nặng có khối lượng M, tác dụng một lực trọng trường P_v = Mg tại điểm B.

Để thanh ngang cân bằng, ta cần xem xét các điều kiện sau:

1. Điều kiện cân bằng tịnh tiến: Tổng lực tác dụng lên thanh phải bằng 0, tức là: \[ P + P_v = P_O + P_A \] Trong đó P_O và P_A là phản lực tại các điểm tựa O và A.
2. Điều kiện cân bằng quay: Tổng momen lực quanh trục O phải bằng 0, tức là: \[ M_v \times d_1 = P_A \times d_2 \] Trong đó M_v là momen lực của vật tại điểm B so với trục quay tại O, P_A là phản lực tại A, và d₂ là khoảng cách từ điểm A tới O.

2. Tính toán momen lực trong đời sống thực tiễn

Ví dụ này minh họa cách tính toán momen lực trong một trường hợp thực tế, chẳng hạn như khi chúng ta sử dụng một cái đòn bẩy để nâng một vật nặng.

• Giả sử một người dùng một thanh gỗ dài 3m làm đòn bẩy để nâng một tảng đá nặng 50kg. Điểm tựa cách tảng đá 0,5m.
• Người này tác dụng một lực F tại đầu còn lại của thanh gỗ để nâng tảng đá.

Ta có thể tính toán lực F cần thiết dựa trên momen lực như sau:

1. Tính momen lực do tảng đá gây ra: \[ M_{\text{đá}} = P_{\text{đá}} \times d_1 = 50 \times 9,8 \times 0,5 = 245 \, \text{Nm} \]
2. Tính lực F cần thiết: \[ F \times d_2 = M_{\text{đá}} \Rightarrow F = \frac{M_{\text{đá}}}{d_2} = \frac{245}{2,5} = 98 \, \text{N} \] Như vậy, lực F cần thiết để nâng tảng đá là 98N.

Qua các ví dụ trên, chúng ta có thể thấy rõ cách momen lực và điều kiện cân bằng của vật được áp dụng trong các tình huống thực tế, từ đó giúp chúng ta hiểu rõ hơn về nguyên lý cơ học quan trọng này.

Momen lực không chỉ là một khái niệm lý thuyết trong vật lý mà còn có rất nhiều ứng dụng thực tiễn trong đời sống hàng ngày, từ các ngành công nghiệp, xây dựng cho đến y tế và các thiết bị gia dụng. Dưới đây là một số ứng dụng quan trọng của momen lực:

1. Ứng dụng trong cơ khí và xây dựng

• Vặn đinh vít và bu lông: Khi vặn một chiếc bu lông hoặc đinh vít, người ta áp dụng momen lực để tạo ra lực quay đủ lớn giúp gắn chặt các bộ phận với nhau. Các công cụ như cờ lê hay tua vít được thiết kế để tăng momen lực bằng cách tăng chiều dài của cánh tay đòn.
• Thanh chắn đường tàu: Momen lực được ứng dụng trong thiết kế thanh chắn tại các giao lộ đường sắt. Khi nâng hoặc hạ thanh chắn, người ta áp dụng momen lực để đảm bảo thanh chắn hoạt động ổn định và an toàn.
• Cẩu trục và cần cẩu: Trong xây dựng, các cần cẩu sử dụng momen lực để nâng và di chuyển các vật liệu nặng. Chiều dài của cần cẩu và lực tác dụng vào điểm đòn bẩy phải được tính toán chính xác để đảm bảo sự cân bằng và an toàn khi vận hành.

2. Ứng dụng trong thiết kế các thiết bị công nghiệp

• Máy móc công nghiệp: Các máy móc như máy tiện, máy khoan, và máy ép sử dụng nguyên lý momen lực để tạo ra các chuyển động quay hoặc nén với lực lớn, phục vụ cho các quy trình sản xuất.
• Khóa vặn và nút xoay: Nguyên lý momen lực được sử dụng để thiết kế các khóa vặn cửa và các nút xoay trong các thiết bị như bếp gas, xe đạp, và ô tô. Việc áp dụng lực tại các điểm cụ thể giúp người dùng dễ dàng điều khiển và vận hành các thiết bị này.
• Đồng hồ đo mômen: Trong công nghiệp, các đồng hồ đo mômen lực được sử dụng để kiểm tra và điều chỉnh lực quay trong các quy trình sản xuất, đảm bảo các sản phẩm được chế tạo với độ chính xác cao.

Các ứng dụng trên không chỉ giúp nâng cao hiệu quả lao động mà còn đảm bảo an toàn trong quá trình sử dụng và vận hành các thiết bị, hệ thống công nghiệp và dân dụng.

Trong phần này, chúng ta sẽ cùng làm quen với các dạng bài tập thực hành về momen lực và điều kiện cân bằng. Các bài tập này không chỉ giúp củng cố kiến thức đã học mà còn phát triển kỹ năng tính toán và phân tích các tình huống thực tế liên quan đến momen lực.

1. Bài tập tính toán momen lực

1. Bài tập 1: Cho một thanh ngang dài \( l = 2 \, m \) có khối lượng không đáng kể, một đầu thanh được gắn chặt vào tường, đầu còn lại chịu tác dụng của một lực \( F = 100 \, N \) vuông góc với thanh. Tính momen lực do lực \( F \) gây ra đối với trục quay tại điểm gắn thanh vào tường.

   Lời giải: Momen lực được tính theo công thức \( M = F \times d \), trong đó \( d \) là khoảng cách từ trục quay đến điểm đặt lực. Ở đây, \( d = l = 2 \, m \). Do đó, momen lực là:

   \[ M = 100 \times 2 = 200 \, N \cdot m \]

2. Bài tập 2: Một cái thang dài \( 4 \, m \) được đặt tựa vào tường, góc giữa thang và mặt đất là \( 60^\circ \). Khối lượng của thang là \( 20 \, kg \), trọng lực tác dụng tại trung điểm của thang. Hãy tính momen lực của trọng lực đối với điểm tựa trên mặt đất.

   Lời giải: Đầu tiên, ta tính khoảng cách từ điểm tựa đến trọng tâm của thang. Khoảng cách này bằng:

   \[ d = \frac{l}{2} \times \sin(60^\circ) = 2 \times \frac{\sqrt{3}}{2} = \sqrt{3} \, m \]

   Momen lực do trọng lực gây ra là:

   \[ M = P \times d = 20 \times 9.8 \times \sqrt{3} \approx 339.6 \, N \cdot m \]

2. Bài tập về điều kiện cân bằng của vật

1. Bài tập 1: Một thanh cứng có khối lượng không đáng kể, dài \( 3 \, m \), đặt nằm ngang và có một điểm tựa ở giữa. Hai vật có khối lượng \( 10 \, kg \) và \( 15 \, kg \) được treo ở hai đầu của thanh. Tìm vị trí của điểm tựa để thanh nằm cân bằng.

   Lời giải: Gọi khoảng cách từ điểm tựa đến vị trí treo vật \( 10 \, kg \) là \( x \). Để thanh cân bằng, momen lực do hai vật gây ra phải bằng nhau, ta có:

   \[ 10 \times 9.8 \times x = 15 \times 9.8 \times (3 - x) \]

   Giải phương trình này, ta tìm được:

   \[ x = 1.8 \, m \]

2. Bài tập 2: Một hệ gồm hai lực có độ lớn bằng nhau là \( 50 \, N \) và cùng tác dụng lên một vật tại hai điểm khác nhau, cách nhau \( 0.5 \, m \). Hãy xác định điều kiện để hệ lực này không làm vật quay.

   Lời giải: Để vật không quay, tổng momen lực do hai lực gây ra phải bằng 0. Vì hai lực có độ lớn bằng nhau nhưng ngược chiều nên điều kiện này tự động được thỏa mãn nếu chúng có cùng cánh tay đòn.

Dưới đây là một số câu hỏi trắc nghiệm giúp bạn ôn tập và củng cố kiến thức về momen lực và điều kiện cân bằng của vật. Các câu hỏi được chia thành nhiều mức độ khác nhau, từ cơ bản đến nâng cao.

1. Câu hỏi trắc nghiệm lý thuyết

1. Hợp lực của hai lực song song cùng chiều là:

   • A. Một lực song song cùng chiều với hai lực và có độ lớn bằng tổng các độ lớn của hai lực thành phần.
   • B. Một lực song song ngược chiều với hai lực và có độ lớn bằng tổng các độ lớn của hai lực thành phần.
   • C. Một lực song song cùng chiều với hai lực và có độ lớn bằng hiệu các độ lớn của hai lực thành phần.
   • D. Một lực song song ngược chiều với hai lực và có độ lớn bằng hiệu các độ lớn của hai lực thành phần.

2. Công thức tính momen lực đối với một trục quay là:

   • A. \( M = F \cdot d \)
   • B. \( M = \frac{F}{d} \)
   • C. \( M = \frac{d}{F} \)
   • D. \( M = F^2 \cdot d \)

3. Phát biểu nào dưới đây về momen lực là đúng?

   • A. Momen lực tác dụng lên vật là đại lượng vô hướng.
   • B. Momen lực được đo bằng tích của lực và cánh tay đòn của nó.
   • C. Momen lực đặc trưng cho độ mạnh yếu của lực tác dụng lên vật.
   • D. Đơn vị của momen lực là N/m.

2. Câu hỏi trắc nghiệm tính toán

1. Một thanh AB dài 2 m được treo ngang, có trục quay cố định tại điểm A. Một lực \( F_1 = 30 \, \text{N} \) tác dụng lên điểm B theo phương vuông góc với thanh. Tính momen lực của lực này đối với trục quay A:

   • A. \( 30 \, \text{N} \cdot m \)
   • B. \( 60 \, \text{N} \cdot m \)
   • C. \( 90 \, \text{N} \cdot m \)
   • D. \( 120 \, \text{N} \cdot m \)

2. Hai lực có độ lớn \( F_1 = 50 \, \text{N} \) và \( F_2 = 70 \, \text{N} \) cùng tác dụng lên một điểm cách nhau 1 m. Tính hợp lực của hai lực này:

   • A. \( 20 \, \text{N} \)
   • B. \( 120 \, \text{N} \)
   • C. \( 80 \, \text{N} \)
   • D. \( 100 \, \text{N} \)