Chủ đề quy tắc momen lực dùng cho: Quy tắc momen lực dùng cho cơ học là một nguyên lý quan trọng, được áp dụng rộng rãi trong nhiều lĩnh vực như kỹ thuật, xây dựng và thể thao. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm, công thức tính toán, cùng với các ứng dụng thực tế của quy tắc momen lực trong đời sống hàng ngày.
Mục lục
Quy Tắc Momen Lực Dùng Cho Cơ Học và Kỹ Thuật
Quy tắc momen lực là một nguyên lý cơ bản trong cơ học, được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau như xây dựng, kỹ thuật cơ khí, thể thao và y học. Nguyên tắc này giúp xác định điều kiện cân bằng của một vật khi có nhiều lực tác dụng lên nó.
Nguyên Tắc Cân Bằng Momen Lực
Để một vật rắn cân bằng, tổng các momen lực tác động lên vật phải bằng không. Điều này có nghĩa là tổng các momen lực làm vật quay theo một chiều phải cân bằng với tổng các momen lực làm vật quay theo chiều ngược lại. Biểu thức toán học của quy tắc này được viết như sau:
\[
\sum M_{\text{clockwise}} = \sum M_{\text{counter-clockwise}}
\]
Công Thức Tính Momen Lực
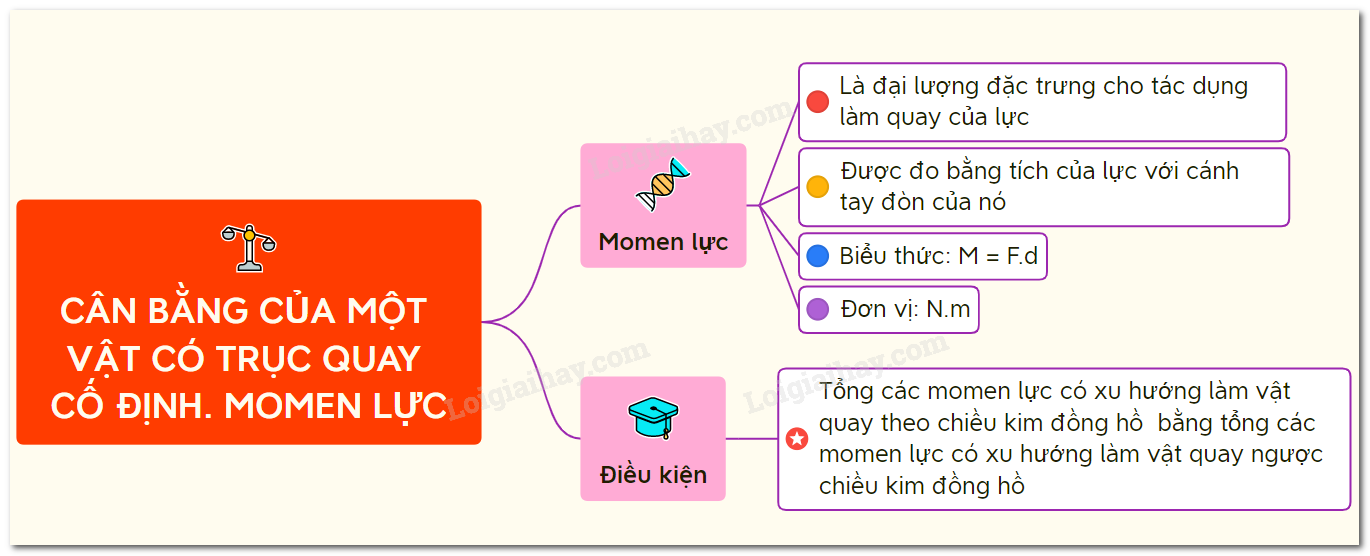
Momen lực là đại lượng đặc trưng cho khả năng làm quay của một lực quanh một trục cố định, được tính bằng công thức:
\[
M = F \cdot d
\]
- M: Momen lực, đơn vị là Newton-mét (N.m)
- F: Lực tác dụng, đơn vị là Newton (N)
- d: Khoảng cách từ điểm tác dụng của lực đến trục quay, đơn vị là mét (m)
Ứng Dụng Thực Tế Của Quy Tắc Momen Lực
- Kỹ thuật cơ khí: Quy tắc momen lực được sử dụng để tính toán và thiết kế các cấu trúc máy móc như cần cẩu, cờ lê, và các loại công cụ khác, giúp tối ưu hóa lực tác động và đảm bảo an toàn trong quá trình vận hành.
- Xây dựng: Trong lĩnh vực xây dựng, quy tắc momen lực được áp dụng để đảm bảo độ bền và ổn định của các công trình như cầu, nhà cao tầng.
- Thể thao: Trong thể thao, như môn golf hoặc cricket, quy tắc momen lực giúp tối ưu hóa kỹ thuật đánh bóng, tăng cường hiệu suất và độ chính xác.
- Y học: Trong y học, quy tắc momen lực được sử dụng để thiết kế các thiết bị y tế như máy trợ lực, đảm bảo tính chính xác và an toàn khi sử dụng.
Ví Dụ Minh Họa
Dưới đây là một số ví dụ về việc áp dụng quy tắc momen lực trong thực tế:
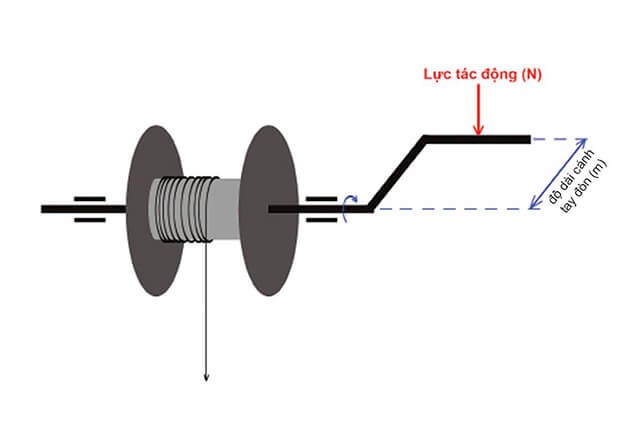
- Thiết kế cờ lê: Khi thiết kế cờ lê, chiều dài của cánh tay đòn được tối ưu hóa để tạo ra momen lực lớn hơn, giúp vặn các đai ốc chặt hơn mà không cần tốn quá nhiều sức.
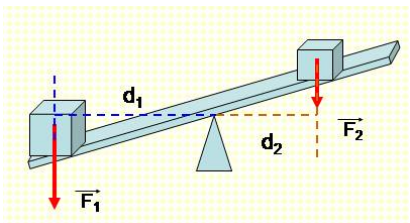
- Hệ thống cân bằng: Trong các hệ thống như cân đòn, các momen lực cần được cân bằng để đảm bảo trạng thái ổn định của hệ thống.
- Nhổ đinh bằng búa: Khi sử dụng búa để nhổ đinh, quy tắc momen lực giúp tính toán lực cần thiết để thực hiện thao tác này một cách hiệu quả.
Bài Tập Vận Dụng Quy Tắc Momen Lực
Dưới đây là một số bài tập ví dụ để bạn có thể vận dụng quy tắc momen lực:
| Bài Tập | Miêu Tả |
|---|---|
| Bài Tập 1 | Một thanh kim loại có chiều dài 2m và khối lượng 10kg, được đặt trên một điểm tựa cách đầu A 0.5m. Tính lực cần thiết để nâng đầu A lên. |
| Bài Tập 2 | Một cần cẩu nâng một vật nặng 500kg bằng một dây cáp dài 3m. Tính momen lực cần thiết để giữ cần cẩu ở trạng thái cân bằng. |
| Bài Tập 3 | Một vận động viên golf tác động một lực 200N lên cây gậy golf dài 1m. Tính momen lực tác dụng lên quả bóng khi gậy golf tiếp xúc với nó. |
Hi vọng với những kiến thức về quy tắc momen lực này, bạn có thể áp dụng vào các bài tập và tình huống thực tế một cách hiệu quả.

.png)
Tổng Quan Về Quy Tắc Momen Lực
Quy tắc momen lực là một nguyên lý cơ bản trong cơ học, giúp xác định điều kiện cân bằng của một vật rắn khi chịu tác động của nhiều lực. Đây là một trong những quy tắc quan trọng nhất để phân tích và giải quyết các bài toán liên quan đến cơ học và kỹ thuật.
Quy tắc này phát biểu rằng, để một vật có trục quay cố định ở trạng thái cân bằng, tổng momen lực tác dụng lên vật theo chiều kim đồng hồ phải bằng tổng momen lực tác dụng ngược chiều kim đồng hồ.
Biểu thức toán học của quy tắc momen lực được mô tả như sau:
\[
\sum M_{\text{clockwise}} = \sum M_{\text{counter-clockwise}}
\]
Trong đó, momen lực (\(M\)) được tính bằng công thức:
\[
M = F \times d
\]
- M: Momen lực, đơn vị là Newton-mét (N.m)
- F: Lực tác dụng, đơn vị là Newton (N)
- d: Khoảng cách từ điểm tác dụng của lực đến trục quay, đơn vị là mét (m)
Quy tắc này không chỉ áp dụng trong các bài toán lý thuyết mà còn được ứng dụng rộng rãi trong thực tế, từ thiết kế các công cụ như cờ lê, búa, đến tính toán trong xây dựng các công trình lớn, và thiết kế các thiết bị cơ khí phức tạp.
Hiểu rõ và vận dụng thành thạo quy tắc momen lực sẽ giúp bạn giải quyết các bài toán về cân bằng lực một cách chính xác và hiệu quả.
Ứng Dụng Của Quy Tắc Momen Lực
Quy tắc momen lực là một nguyên lý quan trọng trong cơ học, và nó có rất nhiều ứng dụng thực tế trong các lĩnh vực khác nhau. Dưới đây là một số ví dụ tiêu biểu về cách áp dụng quy tắc này trong thực tế:
- Kỹ thuật cơ khí: Trong lĩnh vực này, quy tắc momen lực được sử dụng để thiết kế và tính toán các bộ phận máy móc, chẳng hạn như cần cẩu, đòn bẩy và các cơ cấu chuyển động. Quy tắc này giúp đảm bảo rằng các thiết kế có thể chịu được các lực tác dụng mà không bị mất cân bằng.
- Xây dựng: Trong xây dựng, quy tắc momen lực được áp dụng để đảm bảo độ ổn định và an toàn của các công trình. Ví dụ, khi thiết kế cầu hoặc tòa nhà cao tầng, các kỹ sư sử dụng quy tắc này để tính toán tải trọng và đảm bảo rằng cấu trúc sẽ không bị lật hoặc sụp đổ dưới tác động của các lực.
- Thể thao: Quy tắc momen lực cũng được áp dụng trong thể thao, đặc biệt là trong các môn yêu cầu sự cân bằng và kỹ thuật cao như thể dục dụng cụ, golf và cưỡi ngựa. Ví dụ, trong môn golf, người chơi cần tính toán momen lực khi vung gậy để có thể đánh bóng đi xa và chính xác nhất.
- Y học: Trong y học, quy tắc momen lực được sử dụng để thiết kế các thiết bị hỗ trợ, như chân tay giả hoặc các thiết bị chỉnh hình. Những thiết bị này cần phải tạo ra các momen lực thích hợp để giúp bệnh nhân di chuyển một cách tự nhiên và hiệu quả.
- Thiết kế phương tiện giao thông: Khi thiết kế các phương tiện giao thông như ô tô, xe máy, quy tắc momen lực được áp dụng để đảm bảo sự ổn định của phương tiện khi di chuyển trên đường, đặc biệt là khi vào cua hoặc phanh gấp.
- Thiết kế robot: Trong lĩnh vực robot học, quy tắc momen lực giúp thiết kế các khớp nối và các bộ phận chuyển động của robot, đảm bảo rằng robot có thể di chuyển chính xác và hiệu quả trong các môi trường khác nhau.
Những ứng dụng này cho thấy tầm quan trọng của quy tắc momen lực trong việc đảm bảo sự cân bằng và ổn định của các hệ thống cơ học trong nhiều lĩnh vực khác nhau. Hiểu và vận dụng quy tắc này một cách chính xác là điều cần thiết để thiết kế và vận hành các công trình và thiết bị một cách an toàn và hiệu quả.

Các Ví Dụ Minh Họa Quy Tắc Momen Lực
Quy tắc momen lực được áp dụng rộng rãi trong nhiều tình huống thực tế. Dưới đây là một số ví dụ minh họa cụ thể giúp bạn hiểu rõ hơn về cách thức hoạt động của quy tắc này:
- Ví dụ 1: Sử dụng cờ lê để siết ốc
Khi sử dụng cờ lê để siết một đai ốc, bạn áp dụng một lực tại đầu của cờ lê. Khoảng cách từ điểm đặt lực đến trục của đai ốc là cánh tay đòn. Momen lực tạo ra được tính theo công thức:
\[
M = F \times d
\]Trong đó, \(F\) là lực bạn áp dụng, và \(d\) là chiều dài của cờ lê. Cờ lê càng dài, momen lực tạo ra càng lớn, giúp bạn dễ dàng siết đai ốc hơn.
- Ví dụ 2: Hệ thống đòn bẩy trong cân bằng
Giả sử bạn có một thanh đòn bẩy với một vật nặng 10 kg treo ở một đầu. Để cân bằng thanh đòn bẩy, bạn cần đặt một lực tại đầu kia của thanh sao cho tổng momen lực ở cả hai phía bằng nhau. Nếu vật nặng cách điểm tựa 1m, thì momen lực do vật nặng tạo ra là:
\[
M_{\text{vật nặng}} = 10 \times 9.81 \times 1 = 98.1 \text{N.m}
\]Để cân bằng, momen lực do lực đặt vào đầu kia phải bằng 98.1 N.m. Điều này giúp xác định được lực cần thiết để giữ thanh đòn bẩy ở trạng thái cân bằng.
- Ví dụ 3: Nhổ đinh bằng búa
Khi nhổ đinh bằng búa, bạn áp dụng một lực ở tay cầm của búa. Khoảng cách từ điểm đặt lực đến trục quay (tức là điểm tiếp xúc của đầu búa với mặt phẳng) tạo ra một momen lực. Càng đẩy tay cầm búa xa, bạn càng tạo ra momen lực lớn hơn, giúp việc nhổ đinh trở nên dễ dàng hơn.
- Ví dụ 4: Cân bằng cầu thăng bằng trong thể dục dụng cụ
Trong môn thể dục dụng cụ, các vận động viên cần duy trì cân bằng trên cầu thăng bằng. Điều này đòi hỏi họ phải kiểm soát momen lực quanh điểm tựa của cơ thể họ trên cầu. Bằng cách điều chỉnh vị trí tay, chân và cơ thể, họ có thể duy trì cân bằng và thực hiện các động tác một cách chính xác.
Những ví dụ trên cho thấy cách quy tắc momen lực có thể được áp dụng trong nhiều tình huống khác nhau, từ những công việc hàng ngày đến các ứng dụng trong kỹ thuật và thể thao. Hiểu rõ quy tắc này sẽ giúp bạn áp dụng chúng hiệu quả hơn trong cuộc sống và công việc.