Chủ đề giải bài tập momen lực: Khám phá cách giải bài tập momen lực một cách chi tiết và dễ hiểu với bài viết này. Bạn sẽ được hướng dẫn từ những khái niệm cơ bản đến các bài tập thực hành giúp nắm vững kiến thức. Đừng bỏ lỡ cơ hội để hiểu rõ hơn về momen lực và áp dụng chúng vào thực tế một cách hiệu quả!
Mục lục
Giải Bài Tập Momen Lực - Tổng Hợp Kiến Thức và Bài Tập Chi Tiết
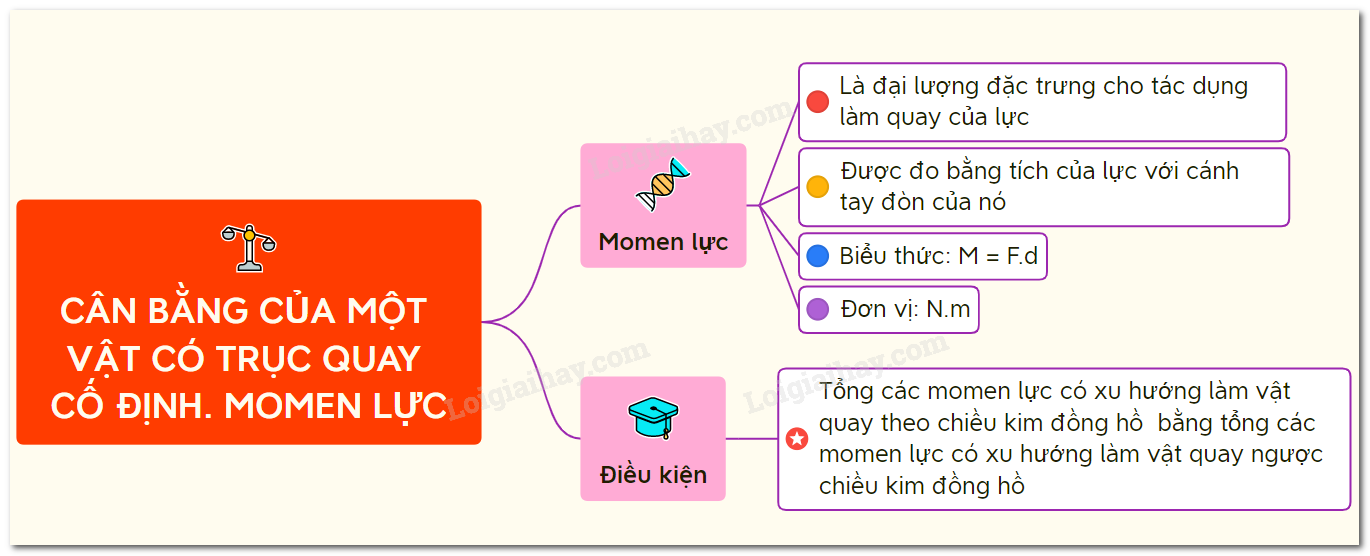
Momen lực là một khái niệm cơ bản trong cơ học, được sử dụng để mô tả khả năng làm quay của một lực quanh một trục cố định. Việc hiểu rõ và áp dụng đúng công thức tính momen lực giúp giải quyết nhiều vấn đề thực tế như mở cửa, vặn ốc vít, hoặc các hệ thống cơ khí phức tạp.
Công Thức Tính Momen Lực
Công thức tính momen lực tổng quát:
Trong đó:
- M: Momen lực
- F: Độ lớn của lực tác dụng
- d: Khoảng cách từ trục quay đến điểm đặt lực (cánh tay đòn)
- θ: Góc giữa phương của lực và cánh tay đòn
Trong trường hợp lực vuông góc với cánh tay đòn, công thức tính momen lực được đơn giản hóa:
Ví Dụ Minh Họa
Ví dụ 1: Một lực có độ lớn 10N tác dụng lên một vật với cánh tay đòn dài 2m và góc giữa lực và cánh tay đòn là 30°. Tính momen lực.
Lời giải:
Các Bài Tập Momen Lực Thường Gặp
Dưới đây là một số dạng bài tập về momen lực thường gặp:
- Bài tập về momen lực khi tác dụng lực lên một vật cố định.
- Bài tập tính momen lực trong hệ thống cơ khí như đòn bẩy, bánh răng.
- Bài tập liên quan đến cân bằng của vật rắn dưới tác dụng của nhiều lực.
Các Bước Giải Bài Tập Momen Lực
- Xác định trục quay của vật: Đây là bước quan trọng để tính toán momen lực chính xác.
- Phân tích và xác định lực tác dụng lên vật: Liệt kê tất cả các lực và xác định khoảng cách từ lực đến trục quay.
- Sử dụng công thức phù hợp: Áp dụng công thức momen lực tùy theo góc giữa lực và cánh tay đòn.
Việc nắm vững các khái niệm và phương pháp giải bài tập momen lực sẽ giúp bạn tự tin giải quyết các bài toán cơ học phức tạp hơn trong thực tế.

.png)
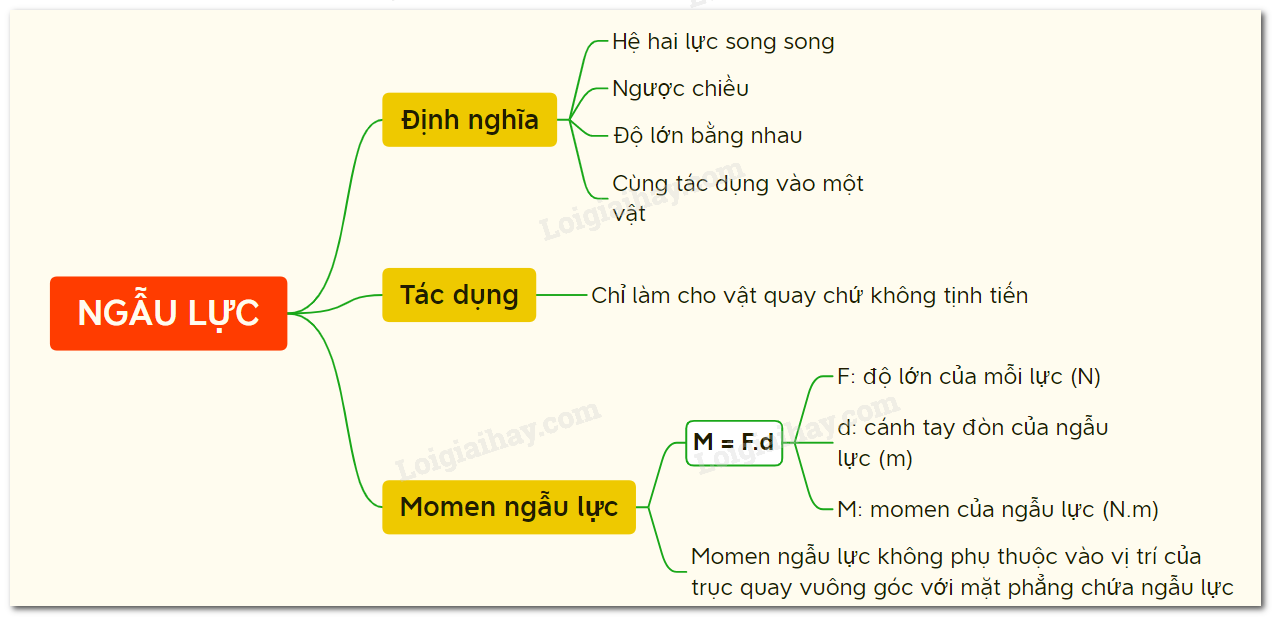
Tổng Quan Về Momen Lực
Momen lực là một khái niệm quan trọng trong vật lý học, liên quan đến khả năng của một lực tác động làm cho một vật quay quanh một trục hoặc điểm cố định. Momen lực được định nghĩa là tích của lực tác dụng và khoảng cách từ điểm đặt lực đến trục quay.
Công thức tính momen lực được biểu diễn dưới dạng:
Trong đó:
- M: Momen lực (đơn vị: N·m)
- F: Lực tác dụng (đơn vị: N)
- d: Khoảng cách từ điểm đặt lực đến trục quay (đơn vị: m)
Momen lực có thể gây ra hai loại chuyển động chính:
- Chuyển động quay: Khi momen lực tác dụng làm cho vật quay quanh trục cố định.
- Chuyển động tịnh tiến: Khi lực tác dụng đồng thời gây ra cả momen lực và chuyển động tịnh tiến.
Trong thực tế, momen lực được ứng dụng rộng rãi trong nhiều lĩnh vực như cơ khí, xây dựng, và kỹ thuật. Hiểu rõ momen lực giúp chúng ta tối ưu hóa thiết kế, cải thiện hiệu suất và đảm bảo an toàn trong các hệ thống cơ khí.
Các Bài Tập Momen Lực Cơ Bản
Các bài tập momen lực cơ bản giúp bạn làm quen với các khái niệm và công thức liên quan đến momen lực, từ đó có thể áp dụng vào các bài toán thực tế. Dưới đây là một số bài tập mẫu cùng với hướng dẫn giải chi tiết.
Bài tập 1: Tính momen lực tác dụng lên một vật.
- Đề bài: Một lực \(F = 10 \, \text{N}\) tác dụng vuông góc lên một thanh dài \(d = 2 \, \text{m}\). Tính momen lực tác dụng lên thanh này.
- Giải: Áp dụng công thức tính momen lực:
- Thay các giá trị vào công thức:
- Kết quả: Momen lực tác dụng lên thanh là \(20 \, \text{N·m}\).
Bài tập 2: Xác định momen lực khi lực không vuông góc với thanh.
- Đề bài: Một lực \(F = 15 \, \text{N}\) tác dụng lên một thanh dài \(d = 3 \, \text{m}\) và tạo góc \( \theta = 30^\circ \) với thanh. Tính momen lực tác dụng lên thanh.
- Giải: Sử dụng công thức momen lực với lực không vuông góc:
- Thay các giá trị vào công thức:
- Kết quả: Momen lực tác dụng lên thanh là \(22.5 \, \text{N·m}\).
Bài tập 3: Tính momen lực trong hệ có nhiều lực tác dụng.
- Đề bài: Một thanh dài \(d = 4 \, \text{m}\) chịu tác dụng của hai lực, lực thứ nhất \(F_1 = 20 \, \text{N}\) ở đầu thanh và lực thứ hai \(F_2 = 10 \, \text{N}\) ở giữa thanh. Tính tổng momen lực tác dụng lên thanh nếu cả hai lực đều vuông góc với thanh.
- Giải: Tính momen lực do từng lực tác dụng:
- Tổng momen lực:
- Kết quả: Tổng momen lực tác dụng lên thanh là \(100 \, \text{N·m}\).

Hướng Dẫn Giải Bài Tập Momen Lực
Khi giải bài tập về momen lực, cần tuân theo các bước cơ bản sau đây để đảm bảo tính chính xác và hiệu quả:
- Xác định lực tác dụng và khoảng cách: Đầu tiên, bạn cần xác định lực tác dụng \(F\) và khoảng cách \(d\) từ điểm tác dụng lực đến trục quay. Lực này có thể là lực vuông góc hoặc lực tạo một góc với thanh.
- Chọn trục quay: Xác định trục quay để tính momen lực. Thường thì trục quay là điểm mà bạn cần tính toán hoặc điểm mà các lực tác dụng không tạo ra momen lực.
- Áp dụng công thức momen lực: Sử dụng công thức \(M = F \times d \times \sin(\theta)\) đối với lực không vuông góc, trong đó \( \theta \) là góc giữa lực và thanh. Đối với lực vuông góc, công thức sẽ là \(M = F \times d\).
- Tính toán từng momen lực: Tính momen lực của từng lực tác dụng lên hệ thống. Nếu có nhiều lực tác dụng, cần tính từng momen lực một.
- Cộng tổng momen lực: Cộng tổng các momen lực lại để tìm momen lực tổng hợp tác dụng lên hệ thống. Chú ý đến dấu của các momen lực (theo chiều kim đồng hồ là âm, ngược chiều kim đồng hồ là dương).
- Giải bài toán: Sau khi có tổng momen lực, áp dụng vào bài toán cụ thể để tìm ra kết quả yêu cầu, ví dụ như tính lực cần thiết, xác định trạng thái cân bằng hoặc tìm momen lực tại một điểm nhất định.
Ví dụ: Một thanh dài 4m chịu tác dụng của một lực vuông góc \(F = 10N\) tại đầu thanh. Tính momen lực:
- Đề bài: Lực \(F = 10N\), khoảng cách \(d = 4m\).
- Giải: Momen lực \(M = F \times d = 10N \times 4m = 40 N·m\).
- Kết quả: Momen lực tác dụng lên thanh là 40 N·m.
Khi đã nắm vững các bước trên, bạn sẽ có thể giải quyết mọi bài tập momen lực một cách hiệu quả và chính xác.
Ví Dụ Minh Họa Giải Bài Tập Momen Lực
Dưới đây là một ví dụ minh họa về cách giải bài tập momen lực để giúp bạn hiểu rõ hơn về khái niệm này:
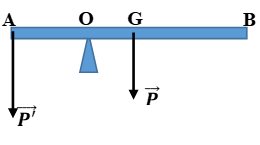
Đề bài: Một thanh cứng dài 3m được đặt ngang trên một trục quay ở một đầu của thanh. Ở đầu còn lại, một lực thẳng đứng \(F = 20N\) tác dụng vuông góc với thanh. Hãy tính momen lực tác dụng lên thanh quanh trục quay.
- Bước 1: Xác định các yếu tố cần thiết:
- Chiều dài thanh: \(d = 3m\)
- Lực tác dụng: \(F = 20N\)
- Lực tác dụng vuông góc với thanh, do đó góc \(\theta = 90^\circ\)
- Bước 2: Áp dụng công thức momen lực:
- Công thức: \(M = F \times d \times \sin(\theta)\)
- Vì \(\theta = 90^\circ\), nên \(\sin(90^\circ) = 1\)
- Tính toán: \(M = 20N \times 3m \times 1 = 60N·m\)
- Bước 3: Kết luận:
- Momen lực tác dụng lên thanh quanh trục quay là 60N·m.
Ví dụ này minh họa cách áp dụng công thức momen lực để tính toán chính xác khi biết các yếu tố như lực tác dụng và khoảng cách từ trục quay. Hãy áp dụng quy trình này cho các bài tập khác để đạt kết quả tốt nhất.

Bài Tập Momen Lực Nâng Cao
Các bài tập momen lực nâng cao yêu cầu sự hiểu biết sâu sắc và khả năng áp dụng kiến thức một cách linh hoạt. Dưới đây là một số bài tập nâng cao với các bước giải chi tiết giúp bạn làm chủ momen lực:
- Bài tập 1:
Một thanh cứng dài \(L = 5m\) có trọng lượng không đáng kể, được đặt trên hai điểm tựa A và B cách nhau \(3m\). Ở vị trí cách A \(2m\), một vật nặng có khối lượng \(m = 10kg\) được treo. Hãy xác định lực tác dụng lên điểm tựa B.
- Xác định các lực tác dụng:
- Lực trọng trường: \(P = m \times g = 10kg \times 9.8m/s^2 = 98N\)
- Lực này tác dụng tại điểm cách A \(2m\)
- Tính momen lực quanh điểm A:
- Momen do trọng lượng: \(M_A = P \times 2m = 98N \times 2m = 196N\cdot m\)
- Momen do lực tác dụng tại B: \(M_B = F_B \times 3m\)
- Cân bằng momen quanh A:
- Vì thanh cân bằng nên \(M_A = M_B\), do đó \(196N\cdot m = F_B \times 3m\)
- Suy ra \(F_B = \frac{196N\cdot m}{3m} = 65.33N\)
- Xác định các lực tác dụng:
- Bài tập 2:
Một thanh có chiều dài \(4m\) với trọng lượng đồng đều \(30N/m\) được đặt ngang qua hai điểm tựa C và D cách nhau \(2m\). Hãy tính lực tác dụng lên các điểm tựa khi một lực \(50N\) tác dụng xuống tại đầu thanh ngoài điểm tựa C.
- Tính trọng lượng toàn thanh:
- Trọng lượng tổng: \(P = 30N/m \times 4m = 120N\)
- Phân tích lực tác dụng và tính momen lực quanh điểm tựa D:
- Momen do trọng lượng: \(M_D = 120N \times 2m = 240N\cdot m\)
- Momen do lực \(50N\): \(M_F = 50N \times 4m = 200N\cdot m\)
- Cân bằng momen: \(F_C \times 2m = M_D + M_F\)
- Suy ra \(F_C = \frac{440N\cdot m}{2m} = 220N\)
- Tính trọng lượng toàn thanh:
Các bài tập trên là những ví dụ tiêu biểu để thực hành và làm chủ momen lực trong các tình huống phức tạp hơn. Hãy đảm bảo nắm vững lý thuyết để giải quyết các bài toán một cách hiệu quả.
XEM THÊM:
Mẹo và Kinh Nghiệm Giải Bài Tập Momen Lực
Giải bài tập momen lực đòi hỏi sự hiểu biết và kỹ năng phân tích sâu sắc. Dưới đây là một số mẹo và kinh nghiệm giúp bạn tiếp cận và giải quyết các bài tập momen lực một cách hiệu quả:
Mẹo Giải Nhanh Bài Tập Momen Lực
- Nhớ rõ công thức cơ bản: Momen lực được tính bằng công thức:
$$\tau = F \cdot d \cdot \sin(\theta)$$
Trong đó,
- F là lực tác dụng
- d là khoảng cách từ trục quay đến điểm đặt lực
- \(\theta\) là góc giữa lực và cánh tay đòn
- Vẽ sơ đồ lực: Trước khi bắt đầu giải, hãy vẽ sơ đồ các lực tác dụng. Điều này giúp bạn dễ dàng hình dung và phân tích các lực trong bài toán.
- Kiểm tra điều kiện vuông góc: Nếu lực tác dụng không vuông góc với cánh tay đòn, hãy chiếu lực theo phương vuông góc để tính toán chính xác momen lực.
- Sử dụng định lý bảo toàn: Khi bài toán có nhiều lực tác dụng, hãy sử dụng định lý bảo toàn momen để đơn giản hóa việc tính toán.
Kinh Nghiệm Xử Lý Bài Tập Momen Lực Khó
- Phân tích kỹ đề bài: Đọc kỹ đề bài và xác định rõ các đại lượng đã cho và cần tìm. Điều này giúp bạn tránh được những sai lầm cơ bản.
- Phân chia bài toán: Đối với các bài toán phức tạp, hãy chia nhỏ bài toán thành các phần dễ giải quyết hơn. Giải từng phần sau đó ghép lại để tìm ra kết quả cuối cùng.
- Sử dụng các công thức liên quan: Đôi khi, bài toán yêu cầu sử dụng các công thức bổ sung như định luật bảo toàn động lượng hoặc năng lượng. Hãy chắc chắn bạn đã nắm vững những công thức này.
- Luyện tập thường xuyên: Để nắm vững các kỹ năng giải bài tập momen lực, không có cách nào tốt hơn là luyện tập thường xuyên. Hãy giải nhiều bài tập từ đơn giản đến phức tạp để nâng cao khả năng của mình.