Chủ đề biểu thức momen lực đối với một trục quay: Biểu thức momen lực đối với một trục quay là kiến thức cơ bản nhưng rất quan trọng trong vật lý và kỹ thuật. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm, công thức, và các ứng dụng thực tế của momen lực, từ đó áp dụng hiệu quả vào học tập và công việc.
Mục lục
Biểu Thức Momen Lực Đối Với Một Trục Quay
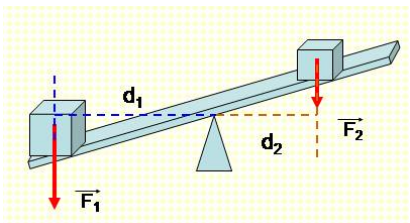
Momen lực là một khái niệm cơ bản trong vật lý, đặc biệt quan trọng trong cơ học. Momen lực đối với một trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực quanh trục đó.
Công Thức Tính Momen Lực
Momen lực được tính bằng công thức:
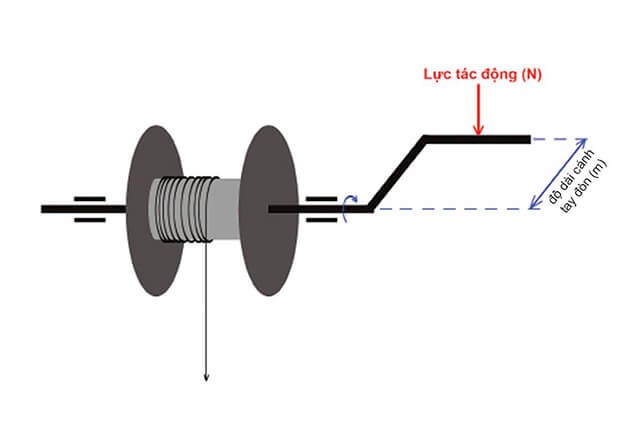
\( M = F \cdot d \)
Trong đó:
- M: Momen lực (đơn vị: Newton-mét, N.m).
- F: Lực tác dụng (đơn vị: Newton, N).
- d: Khoảng cách từ trục quay đến điểm đặt lực (đơn vị: mét, m).
Đơn Vị Đo Lường Momen Lực
Đơn vị đo momen lực là Newton-mét (N.m). Đây là đơn vị kết hợp giữa lực (Newton) và khoảng cách (mét) từ trục quay đến điểm tác động của lực.
Ứng Dụng Thực Tế Của Momen Lực
Momen lực có nhiều ứng dụng trong cả đời sống hàng ngày và công nghiệp, chẳng hạn như:
- Kỹ thuật cơ khí: Tính toán momen lực để thiết kế và vận hành các máy móc như cần cẩu, giúp chúng nâng và di chuyển tải trọng một cách hiệu quả.
- Xây dựng: Dùng momen lực để thiết kế các công trình như cầu, nhà cao tầng, đảm bảo chúng chịu được tải trọng và các lực khác mà không bị sụp đổ.
- Thiết bị gia dụng: Trong các thiết bị như máy xay, máy giặt, momen lực giúp chúng hoạt động trơn tru và hiệu quả.
- Phương tiện giao thông: Momen lực được sử dụng trong thiết kế ô tô và máy bay để đảm bảo khả năng cân bằng và điều khiển phương tiện tốt hơn.
- Thể thao: Trong các môn như golf hay cricket, hiểu biết về momen lực giúp tối ưu hóa lực tác động và điểm tác động, cải thiện kỹ năng chơi.
Quy Tắc Momen Lực
Quy tắc momen lực là một nguyên tắc cơ bản trong cơ học, xác định điều kiện cân bằng của một vật có trục quay cố định. Để một vật rắn cân bằng, tổng momen lực tác động lên vật phải bằng không:
\( \sum M_{\text{clockwise}} = \sum M_{\text{counter-clockwise}} \)
Điều này nghĩa là các momen lực gây ra chuyển động quay theo một chiều phải cân bằng với các momen lực gây ra chuyển động quay theo chiều ngược lại.
Ví Dụ Về Momen Lực
Giả sử có một vật nặng đặt ở một đầu của đòn bẩy và một vật khác ở đầu kia. Nếu chiều dài cánh tay đòn của hai vật khác nhau, trọng lượng của chúng cũng cần được điều chỉnh để đảm bảo cân bằng, tức là momen lực của chúng phải bằng nhau.
| Trường hợp | Công Thức Momen Lực | Kết Quả |
| Momen lực với cánh tay đòn vuông góc | \( M = F \cdot d \) | M đạt giá trị lớn nhất |
| Momen lực với cánh tay đòn không vuông góc | \( M = F \cdot d \cdot \cos(\theta) \) | Giá trị M nhỏ hơn |

.png)
1. Khái niệm Momen Lực
Momen lực là một đại lượng vật lý quan trọng, thể hiện tác dụng làm quay của lực quanh một trục cố định. Nó là một khái niệm cơ bản trong cơ học, đặc biệt trong việc phân tích các hệ thống chuyển động quay.
Momen lực được xác định dựa trên hai yếu tố chính:
- Lực tác dụng (\(F\)): Đây là lực gây ra tác dụng quay, được đo bằng Newton (N).
- Khoảng cách từ trục quay đến điểm đặt lực (\(d\)): Khoảng cách này còn được gọi là cánh tay đòn, được đo bằng mét (m).
Momen lực được tính bằng công thức:
\( M = F \cdot d \)
Trong đó:
- M: Momen lực (đơn vị là Newton-mét, N·m).
- F: Lực tác dụng (đơn vị là Newton, N).
- d: Khoảng cách từ trục quay đến điểm đặt lực (đơn vị là mét, m).
Khi lực tác dụng lên một vật có xu hướng làm cho vật quay quanh một trục cố định, momen lực sẽ quyết định mức độ mạnh yếu của tác dụng quay đó. Nếu lực tác dụng vuông góc với cánh tay đòn, momen lực sẽ đạt giá trị lớn nhất.
Khái niệm momen lực có vai trò quan trọng trong việc thiết kế và vận hành các hệ thống cơ học, giúp tối ưu hóa hiệu quả hoạt động của máy móc và thiết bị.
2. Công Thức Tính Momen Lực
Momen lực là một đại lượng quan trọng trong cơ học, dùng để xác định khả năng của một lực làm quay một vật quanh một trục cố định. Công thức tính momen lực được thiết lập dựa trên mối quan hệ giữa lực tác dụng và khoảng cách từ trục quay đến điểm đặt lực.
Công thức tính momen lực được biểu diễn như sau:
\( M = F \cdot d \)
Trong đó:
- M: Momen lực (đơn vị là Newton-mét, N·m).
- F: Lực tác dụng lên vật (đơn vị là Newton, N).
- d: Khoảng cách từ trục quay đến điểm đặt lực, hay còn gọi là cánh tay đòn (đơn vị là mét, m).
Để áp dụng công thức này một cách chính xác, cần lưu ý các yếu tố sau:
- Hướng của lực tác dụng: Lực phải tác dụng theo hướng vuông góc với cánh tay đòn để tạo ra momen lực lớn nhất. Nếu lực không vuông góc, ta chỉ tính đến thành phần lực vuông góc với cánh tay đòn.
- Vị trí của trục quay: Nếu điểm đặt lực nằm trên đường thẳng đi qua trục quay (khoảng cách \(d = 0\)), momen lực sẽ bằng 0.
- Chiều quay: Momen lực có thể là dương hoặc âm, tùy thuộc vào chiều quay mà lực gây ra (theo chiều kim đồng hồ hoặc ngược chiều kim đồng hồ).
Dưới đây là một số ví dụ minh họa:
| Trường hợp | Công Thức Momen Lực | Kết Quả |
| Lực vuông góc với cánh tay đòn | \( M = F \cdot d \) | Momen lực đạt giá trị lớn nhất |
| Lực không vuông góc với cánh tay đòn | \( M = F \cdot d \cdot \sin(\theta) \) | Giá trị momen lực giảm |
| Lực đi qua trục quay | \( M = 0 \) | Momen lực bằng 0 |
Công thức tính momen lực là công cụ quan trọng giúp trong việc phân tích và thiết kế các hệ thống cơ học, đảm bảo rằng các lực tác động lên hệ thống có thể được quản lý và kiểm soát hiệu quả.

3. Quy Tắc Momen Lực
Quy tắc momen lực là một nguyên tắc cơ bản trong cơ học, được sử dụng để xác định điều kiện cân bằng của một vật thể có trục quay cố định. Khi một vật chịu tác động của nhiều lực khác nhau, quy tắc momen lực giúp xác định khi nào vật sẽ ở trạng thái cân bằng.
Để hiểu rõ hơn về quy tắc này, ta cần nắm vững các khái niệm sau:
- Chiều của momen lực: Momen lực có thể làm vật quay theo chiều kim đồng hồ hoặc ngược chiều kim đồng hồ. Quy ước thường dùng là momen lực theo chiều kim đồng hồ là âm, và ngược chiều kim đồng hồ là dương.
- Tổng momen lực: Để một vật cân bằng, tổng momen lực tác động lên vật phải bằng không. Điều này có nghĩa là tổng các momen lực gây quay theo chiều kim đồng hồ phải bằng tổng các momen lực gây quay ngược chiều kim đồng hồ.
Quy tắc momen lực được biểu diễn dưới dạng:
\( \sum M_{\text{clockwise}} = \sum M_{\text{counter-clockwise}} \)
Điều này có nghĩa là:
- Xác định các lực tác dụng lên vật và khoảng cách từ trục quay đến điểm đặt lực.
- Tính momen lực của từng lực bằng công thức \( M = F \cdot d \cdot \sin(\theta) \), trong đó \( \theta \) là góc giữa lực và cánh tay đòn.
- Cộng tất cả các momen lực theo chiều kim đồng hồ và ngược chiều kim đồng hồ.
- So sánh tổng momen lực theo hai chiều; nếu chúng bằng nhau, vật ở trạng thái cân bằng.
Dưới đây là một ví dụ minh họa cho quy tắc momen lực:
| Lực tác dụng | Khoảng cách (m) | Momen Lực (N·m) | Chiều quay |
| 50 N | 2 m | 100 N·m | Ngược chiều kim đồng hồ |
| 40 N | 2.5 m | 100 N·m | Theo chiều kim đồng hồ |
Trong ví dụ trên, tổng momen lực theo chiều kim đồng hồ bằng tổng momen lực ngược chiều kim đồng hồ, do đó vật sẽ ở trạng thái cân bằng.

XEM THÊM:
4. Ứng Dụng Thực Tiễn của Momen Lực
Momen lực không chỉ là một khái niệm lý thuyết trong vật lý mà còn có rất nhiều ứng dụng trong các lĩnh vực khác nhau của cuộc sống hàng ngày, kỹ thuật cơ khí, và công nghiệp. Dưới đây là một số ứng dụng tiêu biểu của momen lực:
4.1. Trong kỹ thuật cơ khí
- Thiết kế máy móc: Momen lực được sử dụng để tính toán và thiết kế các máy móc công nghiệp như cần cẩu, cánh tay robot, và băng tải. Nó giúp xác định lực cần thiết để nâng, xoay, và di chuyển các tải trọng một cách an toàn và hiệu quả.
- Động cơ ô tô: Momen lực đóng vai trò quan trọng trong việc tối ưu hóa động cơ, giúp xác định lực kéo và hiệu suất vận hành của xe, qua đó ảnh hưởng đến khả năng tăng tốc và sức mạnh của xe.
4.2. Trong xây dựng
- Thiết kế công trình: Trong ngành xây dựng, momen lực được tính toán để đảm bảo các công trình như cầu, nhà cao tầng có khả năng chịu được các tải trọng từ gió, động đất và các tác động khác mà không bị sụp đổ. Momen lực giúp đảm bảo tính ổn định và an toàn của các kết cấu xây dựng.
4.3. Trong đời sống hàng ngày
- Cửa ra vào: Momen lực được áp dụng trong thiết kế tay nắm cửa, giúp việc mở cửa trở nên dễ dàng hơn bằng cách tối ưu hóa vị trí của tay nắm để tăng cánh tay đòn.
- Dụng cụ cầm tay: Các dụng cụ như cờ lê, tua vít đều sử dụng momen lực để tạo ra lực xoay, giúp vặn các ốc vít và mở các chi tiết kết nối một cách hiệu quả.
- Thể thao: Trong thể thao, đặc biệt là các môn như bóng đá và golf, momen lực được sử dụng để tối ưu hóa lực tác động lên bóng, giúp tăng độ chính xác và hiệu quả của các cú đánh.
Những ứng dụng này chỉ là một phần nhỏ trong vô vàn các ứng dụng của momen lực trong đời sống và công nghiệp. Sự hiểu biết và ứng dụng chính xác momen lực có thể mang lại những cải tiến đáng kể trong thiết kế và vận hành của các hệ thống cơ học và công trình xây dựng.

5. Các Lưu Ý Khi Tính Toán Momen Lực
Khi tính toán momen lực đối với một trục quay, có một số lưu ý quan trọng cần phải xem xét để đảm bảo độ chính xác và an toàn trong quá trình thiết kế và ứng dụng. Dưới đây là những lưu ý quan trọng:
5.1. Trường hợp cánh tay đòn vuông góc
Khi lực tác dụng vuông góc với cánh tay đòn, công thức tính momen lực đơn giản nhất là:
\[
M = F \cdot d
\]
Trong đó:
- M: Momen lực (Newton mét - N.m)
- F: Lực tác dụng (Newton - N)
- d: Khoảng cách từ trục quay đến điểm tác dụng của lực (mét - m)
Trường hợp này, momen lực đạt giá trị lớn nhất khi lực tác dụng và cánh tay đòn vuông góc với nhau.
5.2. Trường hợp cánh tay đòn không vuông góc
Nếu lực tác dụng không vuông góc với cánh tay đòn, thì chỉ thành phần vuông góc của lực tham gia vào việc tạo momen. Khi đó, công thức cần điều chỉnh như sau:
\[
M = F \cdot d \cdot \sin(\theta)
\]
Trong đó:
- \(\theta\): Góc giữa lực tác dụng và cánh tay đòn.
Điều này có nghĩa là nếu góc \(\theta\) khác 90 độ, momen lực sẽ nhỏ hơn giá trị tối đa. Do đó, cần chú ý xác định đúng góc \(\theta\) trong quá trình tính toán để đảm bảo độ chính xác.
5.3. Ảnh hưởng của điều kiện môi trường
- Nhiệt độ và độ ẩm: Các yếu tố môi trường như nhiệt độ cao, độ ẩm có thể ảnh hưởng đến vật liệu của cánh tay đòn hoặc trục quay, dẫn đến thay đổi trong các đặc tính cơ học và do đó ảnh hưởng đến momen lực.
- Sự ăn mòn: Trong môi trường có chất ăn mòn, cánh tay đòn và trục quay có thể bị giảm tuổi thọ và độ bền, ảnh hưởng trực tiếp đến momen lực được tạo ra.
5.4. Độ chính xác trong đo lường
- Công cụ đo: Sử dụng các công cụ đo lường chính xác là cần thiết để xác định đúng giá trị lực và cánh tay đòn.
- Sai số: Luôn cần tính đến sai số trong đo lường, đặc biệt là trong các ứng dụng yêu cầu độ chính xác cao.
Việc hiểu và áp dụng đúng các lưu ý trên sẽ giúp đảm bảo rằng momen lực được tính toán một cách chính xác và ứng dụng hiệu quả trong thực tiễn.
6. Tài Liệu Tham Khảo và Học Tập Về Momen Lực
Để hiểu rõ hơn về momen lực và các ứng dụng của nó, việc tham khảo các tài liệu học tập và nguồn tài nguyên trực tuyến là vô cùng quan trọng. Dưới đây là một số nguồn tài liệu và cách học tập hiệu quả về momen lực:
6.1. Sách giáo khoa và tài liệu học tập
- Sách giáo khoa Vật Lý: Sách giáo khoa Vật Lý trung học phổ thông cung cấp nền tảng kiến thức cơ bản về momen lực, bao gồm các khái niệm, định luật và công thức liên quan. Đây là nguồn tài liệu chính thống giúp học sinh nắm vững kiến thức lý thuyết.
- Giáo trình Đại học: Các giáo trình Vật Lý cơ bản và cơ học lý thuyết ở bậc đại học thường trình bày chi tiết hơn về momen lực, bao gồm các ví dụ phức tạp và bài tập thực hành. Một số giáo trình nổi tiếng có thể tham khảo là "Cơ học lý thuyết" và "Vật lý đại cương".
- Sách chuyên ngành: Đối với các chuyên gia và kỹ sư, các sách chuyên ngành như "Cơ học ứng dụng" và "Cơ học kết cấu" cung cấp cái nhìn sâu sắc về cách áp dụng momen lực trong thực tế công việc.
6.2. Nguồn tài nguyên trực tuyến
- Website giáo dục: Các trang web như và cung cấp các bài giảng, video và bài tập về momen lực, phù hợp cho học sinh và sinh viên tự học.
- Video bài giảng trên YouTube: Nhiều kênh giáo dục trên YouTube như Vật Lý 12, Vật Lý Cơ Học cung cấp các video bài giảng chi tiết về momen lực, giúp người học dễ dàng tiếp cận và hiểu rõ hơn về khái niệm này.
- Diễn đàn học tập: Tham gia các diễn đàn như hoặc các nhóm học tập trên mạng xã hội giúp bạn trao đổi và thảo luận với các bạn học khác về những vấn đề liên quan đến momen lực.
Việc kết hợp giữa tài liệu in ấn và nguồn tài nguyên trực tuyến sẽ giúp bạn có cái nhìn toàn diện hơn về momen lực, từ đó áp dụng hiệu quả trong học tập và công việc thực tế.