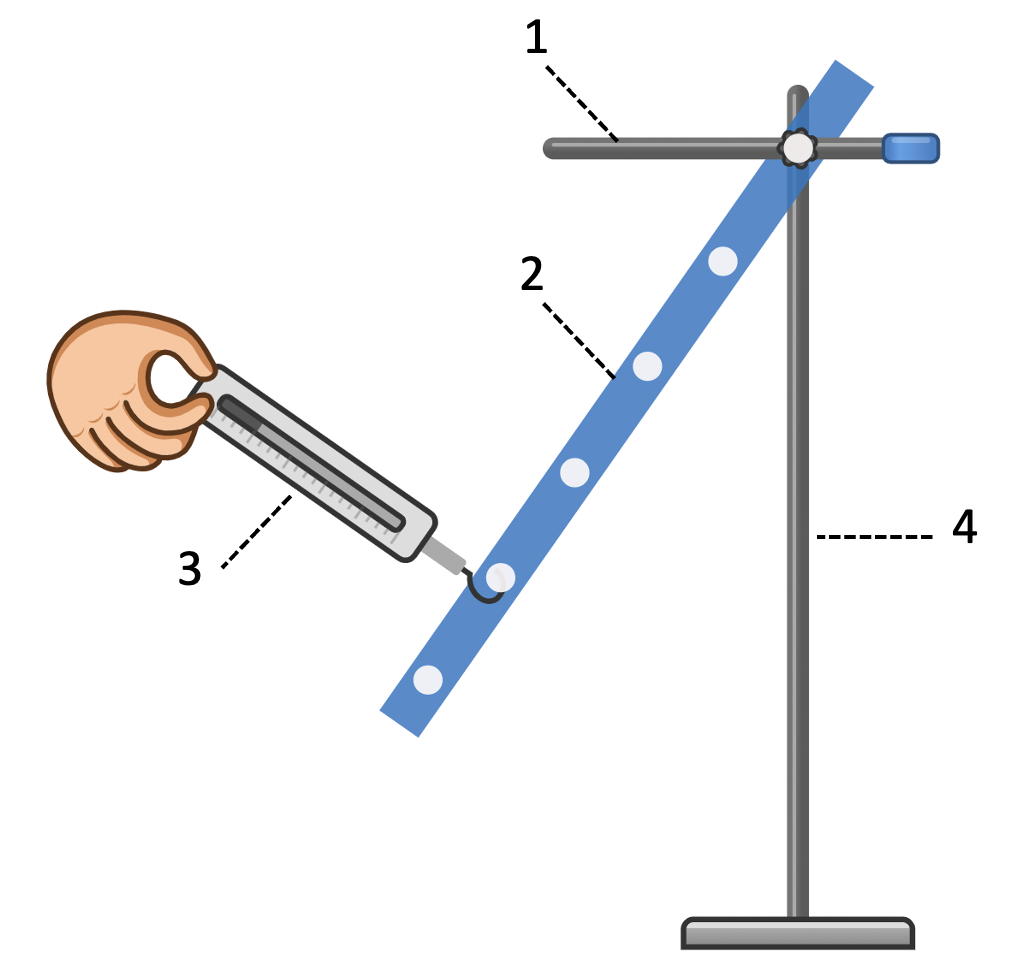
Chủ đề momen lực ví dụ: Momen lực là khái niệm cơ bản trong vật lý học, thể hiện sự ảnh hưởng của lực lên vật thể quanh một trục quay. Bài viết này cung cấp các ví dụ minh họa thực tế về momen lực, giúp bạn hiểu rõ hơn về cách tính toán và ứng dụng momen lực trong đời sống và kỹ thuật.
Mục lục
Momen Lực: Khái Niệm, Công Thức và Ví Dụ Ứng Dụng
Momen lực là một khái niệm cơ bản trong vật lý và kỹ thuật, mô tả khả năng làm quay của một lực đối với một vật quanh một trục cố định. Momen lực được tính bằng công thức:
Trong đó:
\( M \) là momen lực (đơn vị: Nm).\( F \) là lực tác dụng (đơn vị: N).\( d \) là khoảng cách từ điểm đặt lực đến trục quay (đơn vị: m).
Ví Dụ Thực Tiễn của Momen Lực
- Mở cửa: Khi bạn mở cửa, lực bạn tác dụng lên tay nắm cửa kết hợp với khoảng cách từ tay nắm đến bản lề tạo ra momen lực. Nếu tay nắm cửa càng xa bản lề, momen lực càng lớn, việc mở cửa càng dễ dàng.
- Vặn vòi nước: Khi bạn xoay vòi nước, bạn tác động một ngẫu lực lên vòi, tạo ra momen xoắn. Điều này làm cho vòi nước xoay quanh trục của nó một cách dễ dàng.
- Động cơ ô tô: Momen xoắn là một yếu tố quan trọng trong động cơ ô tô, thể hiện sức mạnh của động cơ khi kéo các vật nặng. Động cơ có momen xoắn lớn sẽ giúp xe vượt qua các trở ngại dễ dàng hơn.
Các Ứng Dụng Thực Tế của Momen Lực
- Thiết kế máy móc: Trong thiết kế các bộ phận máy móc, momen lực được sử dụng để đảm bảo các bộ phận hoạt động hiệu quả, ví dụ như việc thiết kế cánh tay nắm cửa sao cho việc mở cửa trở nên dễ dàng hơn.
- Kỹ thuật xây dựng: Momen lực được sử dụng để phân tích và thiết kế các cấu trúc như cần cẩu, cầu và các kết cấu chịu lực khác nhằm đảm bảo chúng có thể chịu được tải trọng mà không bị sụp đổ.
- Cơ học ô tô: Momen xoắn trong động cơ ô tô giúp đánh giá khả năng của xe khi phải tải nặng, làm cho việc di chuyển trên các địa hình khó khăn trở nên hiệu quả hơn.
Quy Tắc Momen Lực
Theo quy tắc momen lực, một vật sẽ ở trạng thái cân bằng khi tổng momen lực tác dụng lên nó bằng 0. Điều này có nghĩa là tổng momen theo chiều kim đồng hồ bằng tổng momen theo chiều ngược lại. Công thức cân bằng momen lực là:
Quy tắc này không chỉ áp dụng cho các vật có trục quay cố định mà còn áp dụng cho các trường hợp không có trục quay cố định, giúp tạo ra trục quay trong những tình huống cụ thể.
Momen lực và các ứng dụng của nó đóng vai trò quan trọng trong nhiều lĩnh vực, từ kỹ thuật đến đời sống hàng ngày, giúp tăng cường hiệu suất và hiệu quả trong nhiều hoạt động khác nhau.

.png)
1. Khái Niệm Momen Lực
Momen lực là đại lượng vật lý mô tả khả năng làm quay của một lực tác dụng lên một vật quanh một trục cố định. Khái niệm này quan trọng trong cơ học và được ứng dụng rộng rãi trong nhiều lĩnh vực như kỹ thuật cơ khí, xây dựng, và đời sống hàng ngày.
Công thức chung để tính momen lực là:
Trong đó:
\( M \) là momen lực (đơn vị: Nm).\( F \) là lực tác dụng lên vật (đơn vị: N).\( d \) là khoảng cách từ trục quay đến điểm tác dụng lực (đơn vị: m).
Momen lực có giá trị dương hoặc âm, phụ thuộc vào hướng quay mà lực tác dụng gây ra. Khi lực làm quay vật theo chiều kim đồng hồ, momen lực thường được xem là âm, và ngược lại, khi lực làm quay vật theo chiều ngược kim đồng hồ, momen lực được coi là dương.
Momen lực có vai trò quan trọng trong nhiều ứng dụng thực tế. Ví dụ, khi mở cửa, lực bạn tác dụng lên tay nắm cửa tạo ra momen lực, làm cho cửa quay quanh bản lề. Hiểu biết về momen lực giúp cải thiện hiệu quả của các thiết kế kỹ thuật và tối ưu hóa sức mạnh cơ học trong các hệ thống khác nhau.
2. Phân Loại Momen Lực
Momen lực có thể được phân loại dựa trên cách mà lực tác động, cũng như tính chất và ứng dụng của chúng trong các lĩnh vực khác nhau. Dưới đây là các phân loại chính của momen lực:
2.1. Momen lực tĩnh và momen lực động
Momen lực tĩnh: Là loại momen lực được sinh ra khi lực tác dụng vào một vật thể đang ở trạng thái tĩnh, không chuyển động. Ví dụ điển hình là khi bạn sử dụng cờ lê để vặn bu-lông nhưng bu-lông không di chuyển, thì momen lực này là tĩnh.
Momen lực động: Là loại momen lực được tạo ra khi lực tác dụng vào một vật thể đang chuyển động. Ví dụ, khi bạn vặn bu-lông và nó bắt đầu xoay, momen lực này là động.
2.2. Momen xoắn và ứng dụng
Momen xoắn: Momen xoắn là loại momen lực được sinh ra khi lực tác dụng làm cho một vật thể quay quanh một trục cố định. Nó thường được sử dụng trong các thiết bị cần chuyển động quay, như động cơ ô tô, máy phát điện, hoặc các thiết bị cơ khí khác.
- Ứng dụng trong động cơ ô tô: Momen xoắn là yếu tố quan trọng quyết định sức mạnh của động cơ, đặc biệt trong việc tăng tốc và di chuyển ở tốc độ thấp.
- Ứng dụng trong máy phát điện: Trong máy phát điện, momen xoắn được sử dụng để tạo ra chuyển động quay, từ đó tạo ra điện năng.
2.3. Momen ngẫu lực
Momen ngẫu lực: Là một cặp lực song song nhưng ngược chiều tác động vào hai điểm khác nhau trên một vật thể, tạo ra một momen làm cho vật thể quay mà không di chuyển vị trí của nó. Ví dụ điển hình là việc vặn tay lái của một chiếc xe đạp.

3. Ứng Dụng Thực Tiễn của Momen Lực
Momen lực có vai trò quan trọng trong nhiều lĩnh vực khác nhau của cuộc sống, từ giao thông, cơ khí đến đời sống hàng ngày. Dưới đây là một số ví dụ tiêu biểu về ứng dụng của momen lực:
- Trong Giao Thông:
- Lái xe ô tô: Momen lực giúp thay đổi hướng di chuyển của xe khi bạn xoay vô lăng, từ đó giúp bạn điều khiển xe dễ dàng và an toàn hơn.
- Đạp phanh xe đạp: Khi bạn đạp phanh, momen lực tác động lên bánh xe, giúp giảm tốc độ và dừng xe một cách hiệu quả.
- Trong Cơ Khí:
- Cần cẩu: Momen lực được sử dụng trong thiết kế và vận hành cần cẩu để nâng và hạ vật nặng một cách an toàn và chính xác.
- Máy móc: Momen lực giúp tối ưu hóa hiệu suất của máy móc, từ động cơ cho đến các thiết bị gia công như máy tiện, máy phay.
- Trong Đời Sống Hàng Ngày:
- Mở cửa: Khi bạn xoay tay nắm cửa, momen lực giúp bạn dễ dàng mở cửa bằng cách vượt qua lực ma sát giữa cửa và khung cửa.
- Kéo đèn trần: Momen lực giúp giữ cho đèn trần ổn định, tránh rung lắc khi bạn kéo dây.
Như vậy, hiểu rõ và áp dụng momen lực trong các hoạt động hàng ngày không chỉ giúp cải thiện hiệu quả mà còn đảm bảo an toàn trong mọi lĩnh vực.

4. Ví Dụ Minh Họa Momen Lực
Dưới đây là một số ví dụ minh họa về momen lực để giúp bạn hiểu rõ hơn về khái niệm này:
- Ví dụ 1: Cân bằng của cân đòn
Khi cân đòn ở trạng thái cân bằng, momen lực do trọng lượng của vật cần đo ở một bên cân sẽ bằng momen lực của quả cân ở bên còn lại. Công thức có thể được viết như sau:
\( M_1 = M_2 \)
Trong đó:
- \( M_1 \): Momen lực của vật cần đo
- \( M_2 \): Momen lực của quả cân
- Ví dụ 2: Sử dụng cờ lê để vặn đai ốc
Khi sử dụng cờ lê để vặn đai ốc, lực tác dụng vào tay cầm của cờ lê tạo ra momen xoắn làm đai ốc quay. Momen xoắn được tính bằng công thức:
\( M = F \times d \)
Trong đó:
- \( F \): Lực tác dụng (N)
- \( d \): Chiều dài của tay cầm (m)
- Ví dụ 3: Dùng búa nhổ đinh
Khi sử dụng búa để nhổ đinh, lực tác dụng lên đầu búa tạo ra momen lực, giúp rút đinh ra khỏi bề mặt. Ví dụ, nếu lực tác dụng là 100 N và khoảng cách từ điểm tác dụng lực đến trục quay là 0.2 m, ta có:
\( M = 100 \times 0.2 = 20 \, Nm \)
- Ví dụ 4: Cửa xoay tự động
Cửa xoay tự động cũng là một ứng dụng của momen lực. Khi tác dụng một lực nhỏ lên cánh cửa, lực này tạo ra momen lực làm cửa quay quanh trục.

5. Quy Tắc Cân Bằng Momen Lực
Quy tắc cân bằng momen lực là nguyên tắc cơ bản trong cơ học, giúp chúng ta xác định điều kiện cân bằng của vật khi có các lực tác động lên nó. Theo quy tắc này, tổng momen lực tác động theo chiều kim đồng hồ phải bằng tổng momen lực tác động ngược chiều kim đồng hồ để vật ở trạng thái cân bằng.
Momen lực được tính bằng công thức:
\(\tau = F \cdot d \cdot \sin{\theta}\)
Trong đó:
- \(F\) là lực tác động (N)
- \(d\) là khoảng cách từ trục quay đến điểm tác dụng lực (m)
- \(\theta\) là góc giữa lực và cánh tay đòn
Điều kiện cân bằng momen lực được diễn tả qua công thức:
\(M_1 = M_2\) hoặc \(F_1 \cdot d_1 = F_2 \cdot d_2\)
Nếu áp dụng vào thực tiễn, ta có thể thấy quy tắc này ở nhiều tình huống như:
- Chiếc bập bênh: Khi hai người ngồi ở hai đầu, bập bênh sẽ cân bằng khi momen lực của họ bằng nhau.
- Việc sử dụng cờ lê để vặn bu lông: Cánh tay đòn càng dài, lực tác dụng càng nhỏ nhưng momen lực lại càng lớn, giúp vặn bu lông dễ dàng hơn.
- Trò chơi kéo co: Đội nào tạo ra momen lực lớn hơn (bằng cách kéo mạnh hơn hoặc đứng xa hơn từ điểm kéo) sẽ giành chiến thắng.
Trong thực tế, quy tắc này giúp chúng ta thiết kế các hệ thống cân bằng và đảm bảo tính ổn định của các kết cấu cơ khí.
XEM THÊM:
6. Lợi Ích và Ý Nghĩa của Momen Lực
Momen lực là một đại lượng quan trọng trong lĩnh vực cơ học, thể hiện khả năng tác động của một lực lên một vật để tạo ra chuyển động quay. Hiểu rõ lợi ích và ý nghĩa của momen lực giúp ta ứng dụng tốt hơn trong nhiều lĩnh vực thực tiễn.
- Trong cơ khí: Momen lực được áp dụng rộng rãi trong việc thiết kế và vận hành các máy móc, từ xe cộ đến các thiết bị công nghiệp. Nó giúp xác định khả năng quay và hiệu suất của các bộ phận máy móc.
- Trong đời sống hàng ngày: Momen lực xuất hiện trong các hoạt động như mở cửa, vặn ốc vít, và thậm chí trong việc xoay chìa khóa. Những thao tác này dựa vào nguyên lý momen lực để tạo ra chuyển động mong muốn.
- Trong giáo dục: Hiểu và áp dụng đúng momen lực giúp học sinh nắm vững kiến thức cơ bản về vật lý, từ đó phát triển khả năng giải quyết các bài toán liên quan đến lực và chuyển động.
- Trong công nghiệp: Momen lực đóng vai trò quan trọng trong việc tính toán và thiết kế các hệ thống truyền động, đảm bảo hiệu suất cao và sự bền bỉ trong hoạt động của các thiết bị công nghiệp.
Nhờ vào momen lực, chúng ta có thể tính toán và thiết kế các hệ thống cơ khí một cách hiệu quả, đảm bảo sự an toàn và hiệu quả trong sử dụng hàng ngày.