Chủ đề động lực học của chuyển động tròn lực hướng tâm: Động lực học của chuyển động tròn và lực hướng tâm là những khái niệm cơ bản nhưng cực kỳ quan trọng trong vật lý học. Bài viết này sẽ giúp bạn hiểu rõ nguyên lý hoạt động, các công thức quan trọng, cùng với những ứng dụng thực tiễn của chúng trong đời sống hàng ngày.
Mục lục
Động Lực Học Của Chuyển Động Tròn Và Lực Hướng Tâm
Động lực học của chuyển động tròn là một lĩnh vực quan trọng trong vật lý học, nghiên cứu về các lực tác dụng lên vật khi chúng di chuyển theo quỹ đạo tròn. Một trong những khái niệm quan trọng trong chủ đề này là lực hướng tâm, lực giữ cho vật chuyển động theo đường tròn bằng cách hướng về tâm của quỹ đạo.
Lực Hướng Tâm
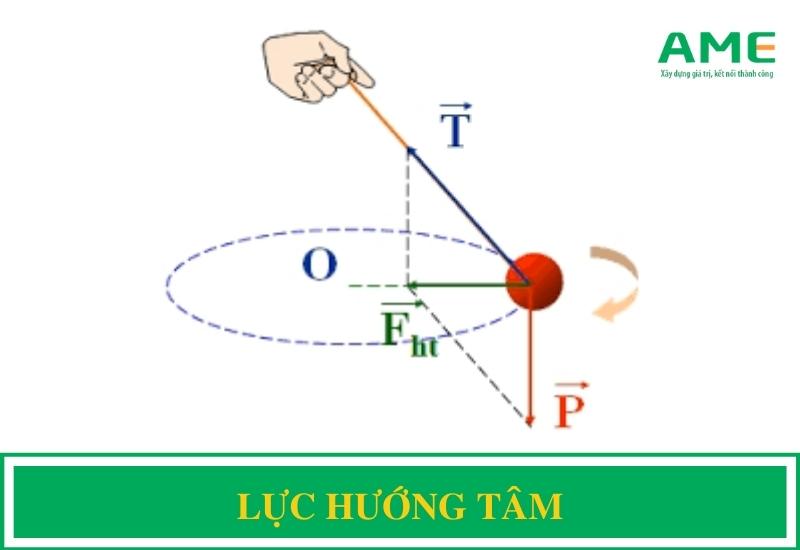
Lực hướng tâm là hợp lực tác dụng lên vật, luôn hướng về phía tâm của quỹ đạo tròn. Công thức của lực hướng tâm được biểu diễn bằng:
\[
F_{ht} = m \cdot a_{ht} = m \cdot \frac{v^2}{R} = m \cdot \omega^2 \cdot R
\]
Trong đó:
- Fht: Lực hướng tâm (N).
- m: Khối lượng của vật (kg).
- aht: Gia tốc hướng tâm (m/s²).
- v: Vận tốc tuyến tính của vật (m/s).
- R: Bán kính của quỹ đạo tròn (m).
- ω: Vận tốc góc (rad/s).
Ứng Dụng Trong Thực Tế
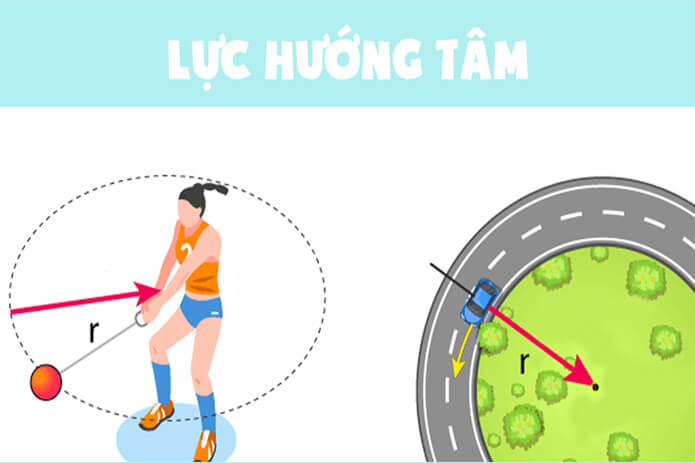
Lực hướng tâm có nhiều ứng dụng trong đời sống hàng ngày, đặc biệt là trong các trường hợp sau:
- Xe chạy trên đường vòng: Khi xe chạy qua khúc cua, lực ma sát giữa lốp xe và mặt đường đóng vai trò là lực hướng tâm giúp xe giữ được quỹ đạo tròn mà không bị trượt khỏi đường.
- Chuyển động của vệ tinh quanh Trái Đất: Vệ tinh di chuyển quanh Trái Đất theo quỹ đạo tròn nhờ lực hấp dẫn đóng vai trò là lực hướng tâm, giữ vệ tinh trong quỹ đạo cố định.
- Trò chơi cảm giác mạnh: Các thiết bị trong công viên giải trí, như vòng quay tốc độ cao, dựa vào lực hướng tâm để giữ an toàn cho người chơi khi chuyển động tròn.
Ví Dụ Minh Họa
Để hiểu rõ hơn về lực hướng tâm, chúng ta cùng xem xét một vài bài toán minh họa:
| Bài toán 1: | Một vật có khối lượng 2 kg di chuyển trên quỹ đạo tròn với bán kính 0,5 m và vận tốc 4 m/s. Tính lực hướng tâm tác dụng lên vật. |
| Giải: | Sử dụng công thức Fht = m \cdot \frac{v^2}{R}, ta có \[ F_{ht} = 2 \cdot \frac{4^2}{0,5} = 64 \text{ N} \] |
| Bài toán 2: | Một vệ tinh có khối lượng 500 kg bay quanh Trái Đất ở độ cao 400 km với bán kính quỹ đạo là 6800 km. Tính lực hướng tâm tác dụng lên vệ tinh. |
| Giải: | Sử dụng công thức Fht = m \cdot \omega^2 \cdot R, với ω = \frac{v}{R}, ta tính được lực hướng tâm. |
Kết Luận
Động lực học của chuyển động tròn và lực hướng tâm là những khái niệm cơ bản trong vật lý học, có ứng dụng rộng rãi trong cả lý thuyết và thực tiễn. Việc nắm vững các kiến thức này sẽ giúp bạn hiểu rõ hơn về các hiện tượng tự nhiên cũng như các ứng dụng công nghệ trong đời sống.

.png)
Mở đầu về Động Lực Học Của Chuyển Động Tròn
Động lực học của chuyển động tròn là một lĩnh vực quan trọng trong vật lý học, tập trung nghiên cứu các lực tác dụng lên vật khi chúng di chuyển theo quỹ đạo tròn. Chuyển động tròn thường gặp trong nhiều hiện tượng tự nhiên và ứng dụng kỹ thuật, từ quỹ đạo của các hành tinh cho đến chuyển động của các thiết bị cơ khí.
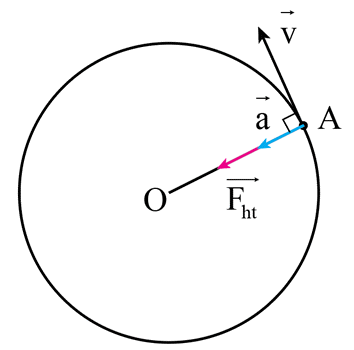
Khi một vật chuyển động theo quỹ đạo tròn, nó luôn chịu tác động của một lực gọi là lực hướng tâm. Lực này giữ cho vật tiếp tục di chuyển theo đường tròn và có phương luôn hướng vào tâm của quỹ đạo. Sự tồn tại của lực hướng tâm là yếu tố quyết định để vật không bị văng ra khỏi quỹ đạo của nó.
Để hiểu rõ hơn, hãy xem xét một vật có khối lượng \( m \) di chuyển với vận tốc \( v \) trên quỹ đạo tròn có bán kính \( R \). Lực hướng tâm \( F_{ht} \) có thể được biểu diễn bằng công thức:
\[
F_{ht} = m \cdot \frac{v^2}{R} = m \cdot \omega^2 \cdot R
\]
Trong đó:
- Fht: Lực hướng tâm (Newton).
- m: Khối lượng của vật (kg).
- v: Vận tốc tuyến tính của vật (m/s).
- R: Bán kính của quỹ đạo tròn (m).
- ω: Vận tốc góc (rad/s).
Sự hiểu biết về động lực học của chuyển động tròn không chỉ quan trọng trong việc phân tích các hiện tượng vật lý mà còn ứng dụng rộng rãi trong kỹ thuật, từ thiết kế các phương tiện giao thông đến điều khiển vệ tinh trong không gian.
Lý Thuyết Và Công Thức Cơ Bản
Trong động lực học của chuyển động tròn, lý thuyết và các công thức cơ bản đóng vai trò quan trọng trong việc hiểu và tính toán các đại lượng liên quan. Dưới đây là một số khái niệm và công thức cơ bản mà bạn cần nắm vững.
1. Gia Tốc Hướng Tâm
Khi một vật chuyển động theo quỹ đạo tròn đều, mặc dù vận tốc có độ lớn không đổi, nhưng hướng của vận tốc luôn thay đổi. Sự thay đổi này tạo ra một gia tốc có hướng luôn hướng về tâm của quỹ đạo, gọi là gia tốc hướng tâm. Gia tốc hướng tâm \(a_{ht}\) được tính bằng công thức:
\[
a_{ht} = \frac{v^2}{R} = \omega^2 \cdot R
\]
Trong đó:
- aht: Gia tốc hướng tâm (m/s²).
- v: Vận tốc tuyến tính của vật (m/s).
- R: Bán kính của quỹ đạo tròn (m).
- ω: Vận tốc góc (rad/s).
2. Lực Hướng Tâm
Lực hướng tâm là lực giữ cho vật di chuyển theo quỹ đạo tròn và có phương luôn hướng về tâm của quỹ đạo. Lực này có thể do nhiều nguyên nhân gây ra như lực hấp dẫn, lực căng dây, hay lực ma sát. Công thức của lực hướng tâm được biểu diễn như sau:
\[
F_{ht} = m \cdot a_{ht} = m \cdot \frac{v^2}{R} = m \cdot \omega^2 \cdot R
\]
Trong đó:
- Fht: Lực hướng tâm (N).
- m: Khối lượng của vật (kg).
- aht: Gia tốc hướng tâm (m/s²).
- v: Vận tốc tuyến tính của vật (m/s).
- R: Bán kính của quỹ đạo tròn (m).
- ω: Vận tốc góc (rad/s).
3. Mối Quan Hệ Giữa Vận Tốc Góc Và Vận Tốc Tuyến Tính
Vận tốc góc \( \omega \) và vận tốc tuyến tính \( v \) có mối quan hệ trực tiếp với nhau, được xác định qua bán kính \( R \) của quỹ đạo tròn:
\[
v = \omega \cdot R
\]
Điều này có nghĩa là khi vận tốc góc không đổi, vật di chuyển trên quỹ đạo có bán kính lớn hơn sẽ có vận tốc tuyến tính lớn hơn.
4. Tần Số Và Chu Kỳ Của Chuyển Động Tròn
Tần số \( f \) và chu kỳ \( T \) là hai đại lượng liên quan đến thời gian trong chuyển động tròn. Chu kỳ là thời gian để vật hoàn thành một vòng tròn, và tần số là số vòng vật đi được trong một giây:
- Chu kỳ: \[ T = \frac{1}{f} \]
- Tần số: \[ f = \frac{1}{T} = \frac{\omega}{2\pi} \]
Hiểu rõ các công thức và lý thuyết cơ bản này giúp bạn nắm bắt được các hiện tượng liên quan đến chuyển động tròn, từ đó ứng dụng chúng vào các bài toán cụ thể và thực tiễn trong cuộc sống.

Các Ứng Dụng Thực Tế
Động lực học của chuyển động tròn và lực hướng tâm không chỉ là lý thuyết trong sách giáo khoa, mà còn có rất nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày và các ngành công nghiệp. Dưới đây là một số ứng dụng tiêu biểu:
1. Ứng Dụng Trong Giao Thông Vận Tải
Trong giao thông, đặc biệt là khi các phương tiện như ô tô, xe máy di chuyển qua các đoạn đường cong, lực hướng tâm đóng vai trò quan trọng để giữ cho phương tiện không bị trượt ra khỏi quỹ đạo. Lực này được tạo ra nhờ ma sát giữa lốp xe và mặt đường, đảm bảo an toàn cho người tham gia giao thông.
2. Chuyển Động Của Vệ Tinh Quanh Trái Đất
Các vệ tinh nhân tạo quay quanh Trái Đất theo quỹ đạo tròn dưới tác động của lực hấp dẫn, đóng vai trò là lực hướng tâm. Lực này giữ cho vệ tinh không bay vào không gian hoặc rơi xuống Trái Đất, giúp vệ tinh duy trì quỹ đạo ổn định để thực hiện các nhiệm vụ như viễn thông, dự báo thời tiết, và quan sát Trái Đất.
3. Thiết Kế Máy Ly Tâm Trong Công Nghệ
Máy ly tâm là một thiết bị phổ biến trong các phòng thí nghiệm và nhà máy sản xuất. Bằng cách quay các mẫu vật với tốc độ cao, lực hướng tâm được tạo ra giúp tách các thành phần khác nhau của mẫu dựa trên khối lượng riêng của chúng. Ứng dụng này rất quan trọng trong y học, công nghiệp thực phẩm, và hóa chất.
4. Trò Chơi Giải Trí Và Công Viên Nước
Trong các trò chơi như vòng quay khổng lồ hay tàu lượn siêu tốc, lực hướng tâm đóng vai trò quan trọng trong việc đảm bảo an toàn cho người chơi. Lực này giúp giữ người chơi ở trên ghế khi tàu lượn đi qua các khúc cua và đảm bảo rằng không ai bị văng ra khỏi đường đi.
5. Ứng Dụng Trong Thể Thao
Trong các môn thể thao như đua xe, đua ngựa, hay trượt băng nghệ thuật, vận động viên cần hiểu và tận dụng lực hướng tâm để duy trì tốc độ và sự ổn định khi di chuyển qua các khúc cua. Kỹ năng kiểm soát lực này có thể quyết định thành công hay thất bại trong các cuộc thi.
Những ứng dụng trên cho thấy sự quan trọng và đa dạng của động lực học của chuyển động tròn và lực hướng tâm trong nhiều lĩnh vực khác nhau của đời sống và công nghệ.

XEM THÊM:
Bài Tập Và Ví Dụ Minh Họa
Để củng cố kiến thức về động lực học của chuyển động tròn và lực hướng tâm, việc thực hành qua các bài tập và ví dụ minh họa là rất cần thiết. Dưới đây là một số bài tập và ví dụ cụ thể nhằm giúp bạn hiểu rõ hơn về các khái niệm này.
1. Bài Tập Tính Lực Hướng Tâm
Đề bài: Một chiếc xe có khối lượng \(m = 1000 \, \text{kg}\) di chuyển với vận tốc \(v = 20 \, \text{m/s}\) trên đường cong có bán kính \(R = 50 \, \text{m}\). Tính lực hướng tâm tác dụng lên xe.
Lời giải: Sử dụng công thức tính lực hướng tâm:
\[
F_{ht} = m \cdot \frac{v^2}{R}
\]
Thay các giá trị đã cho vào công thức:
\[
F_{ht} = 1000 \cdot \frac{20^2}{50} = 8000 \, \text{N}
\]
Vậy, lực hướng tâm tác dụng lên xe là \(8000 \, \text{N}\).
2. Ví Dụ Về Chuyển Động Của Vệ Tinh Quanh Trái Đất
Đề bài: Một vệ tinh có khối lượng \(m = 500 \, \text{kg}\) chuyển động tròn đều quanh Trái Đất ở độ cao sao cho bán kính quỹ đạo \(R = 7000 \, \text{km}\). Tính vận tốc của vệ tinh biết rằng gia tốc hướng tâm bằng gia tốc trọng trường \(g = 9,8 \, \text{m/s}^2\).
Lời giải: Gia tốc hướng tâm được tính bằng công thức:
\[
a_{ht} = \frac{v^2}{R}
\]
Do đó:
\[
v^2 = g \cdot R
\]
Thay giá trị vào công thức:
\[
v^2 = 9,8 \cdot 7 \times 10^6
\]
Suy ra:
\[
v = \sqrt{6,86 \times 10^7} \approx 8,28 \times 10^3 \, \text{m/s}
\]
Vậy, vận tốc của vệ tinh là khoảng \(8280 \, \text{m/s}\).
3. Bài Tập Về Lực Hướng Tâm Trong Chuyển Động Tròn Đều
Đề bài: Một vật có khối lượng \(m = 2 \, \text{kg}\) quay trên quỹ đạo tròn bán kính \(R = 0,5 \, \text{m}\) với vận tốc góc \( \omega = 10 \, \text{rad/s}\). Tính lực hướng tâm tác dụng lên vật.
Lời giải: Lực hướng tâm được tính theo công thức:
\[
F_{ht} = m \cdot \omega^2 \cdot R
\]
Thay các giá trị đã cho vào công thức:
\[
F_{ht} = 2 \cdot 10^2 \cdot 0,5 = 100 \, \text{N}
\]
Vậy, lực hướng tâm tác dụng lên vật là \(100 \, \text{N}\).
Thông qua các bài tập và ví dụ minh họa trên, bạn có thể nắm vững hơn về cách áp dụng các công thức động lực học trong chuyển động tròn và lực hướng tâm vào các tình huống thực tế. Điều này không chỉ giúp tăng cường kiến thức mà còn phát triển kỹ năng giải quyết vấn đề trong vật lý học.