Lực Hướng Tâm và Gia Tốc Hướng Tâm Bài 32: Khám Phá Toàn Diện và Ứng Dụng Thực Tế

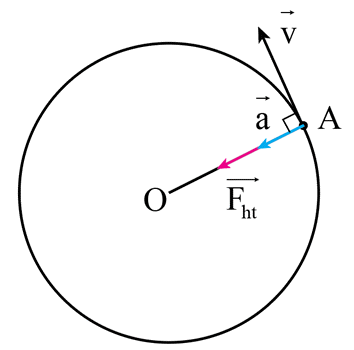
Lực hướng tâm là lực tác dụng vào một vật đang chuyển động tròn đều, hướng vào tâm của quỹ đạo chuyển động. Lực này là nguyên nhân chính khiến cho vật duy trì chuyển động tròn đều quanh một điểm cố định.

I. Lực Hướng Tâm

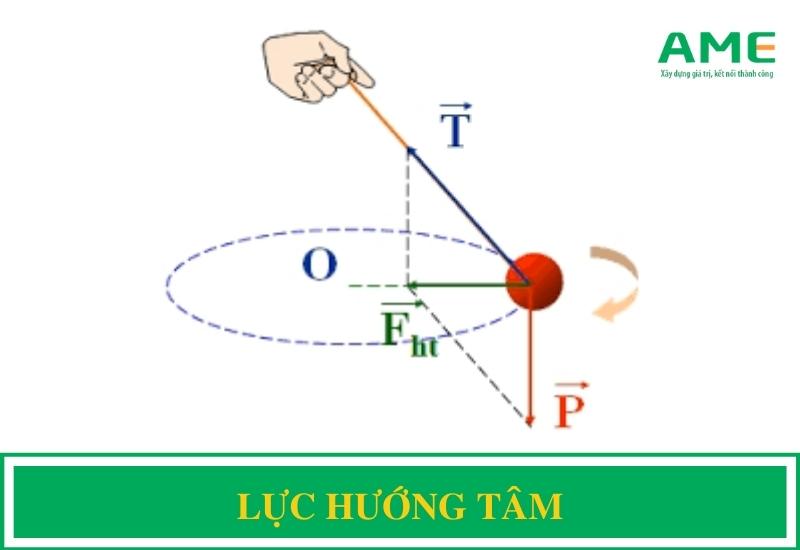
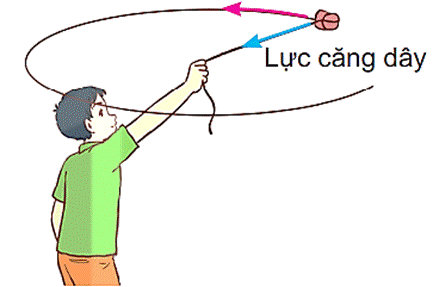
Khi một vật chuyển động tròn đều, lực tác dụng làm vật chuyển động trong quỹ đạo tròn được gọi là lực hướng tâm. Ví dụ, khi ta buộc một vật vào đầu dây và quay tròn trong mặt phẳng ngang, lực căng dây đóng vai trò là lực hướng tâm.

• Lực hướng tâm: Là lực gây ra sự thay đổi hướng chuyển động của vật, luôn hướng vào tâm quỹ đạo.
• Ví dụ về lực hướng tâm: Lực hấp dẫn của Trái Đất tác dụng lên Mặt Trăng khiến Mặt Trăng quay quanh Trái Đất.

II. Gia Tốc Hướng Tâm

Gia tốc hướng tâm là gia tốc mà vật chịu tác dụng khi nó chuyển động tròn đều, có phương hướng vào tâm của quỹ đạo. Công thức tính gia tốc hướng tâm là:

$$


a
ht

=


v
2

r

=

ω
2

r

• a_ht: Gia tốc hướng tâm (m/s²).
• v: Vận tốc của vật (m/s).
• r: Bán kính của quỹ đạo chuyển động (m).

III. Công Thức Độ Lớn Lực Hướng Tâm

Độ lớn của lực hướng tâm được tính theo công thức:

$$


F
ht

=


m

v
2


r

=
m

ω
2

r

• F_ht: Lực hướng tâm (N).
• m: Khối lượng của vật (kg).

IV. Ứng Dụng Thực Tế

• Chuyển động của các hành tinh quanh Mặt Trời là kết quả của lực hấp dẫn đóng vai trò là lực hướng tâm.
• Gia tốc hướng tâm cũng có thể được thấy trong các hệ thống như bánh xe ô tô khi chúng quay, lực căng dây giữ cho con quay di chuyển tròn.

Lực hướng tâm là một khái niệm quan trọng trong vật lý, đặc biệt là khi nghiên cứu về chuyển động tròn đều. Lực này đóng vai trò chính trong việc duy trì quỹ đạo tròn của một vật thể bằng cách liên tục hướng lực vào tâm của quỹ đạo đó.

1. Khái niệm Lực Hướng Tâm

Lực hướng tâm được định nghĩa là lực (hoặc tổng hợp lực) tác dụng lên một vật thể đang chuyển động theo quỹ đạo tròn và luôn hướng vào tâm của quỹ đạo này. Nó là yếu tố quyết định giữ cho vật thể không bay ra khỏi quỹ đạo do quán tính của nó.

2. Ví dụ về Lực Hướng Tâm trong Thực Tế

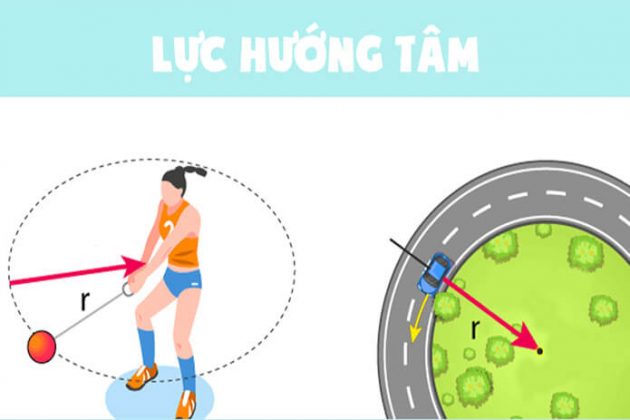
• Lực căng dây: Khi một vật thể được buộc vào đầu dây và quay tròn, lực căng của dây đóng vai trò là lực hướng tâm.
• Lực hấp dẫn: Trường hợp lực hấp dẫn giữa Trái Đất và Mặt Trăng, lực hấp dẫn này chính là lực hướng tâm giữ cho Mặt Trăng quay quanh Trái Đất.
• Lực ma sát: Trong một số trường hợp, lực ma sát giữa bánh xe và mặt đường có thể đóng vai trò như lực hướng tâm, giữ cho xe không trượt ra ngoài khi vào cua.

3. Tầm Quan Trọng của Lực Hướng Tâm trong Chuyển Động Tròn

Lực hướng tâm là yếu tố không thể thiếu để duy trì chuyển động tròn đều. Nếu không có lực hướng tâm, vật thể sẽ di chuyển theo đường thẳng ra ngoài do quán tính. Vì vậy, trong mọi tình huống mà vật thể có xu hướng di chuyển theo quỹ đạo tròn, cần phải có một lực đủ lớn hướng về tâm để cân bằng và duy trì chuyển động này.

Trong thực tiễn, lực hướng tâm được ứng dụng rộng rãi, từ việc thiết kế các hệ thống cơ học như vòng quay, bánh răng, cho đến việc nghiên cứu quỹ đạo của các thiên thể trong vũ trụ.

Để giải quyết các bài toán liên quan đến lực hướng tâm và gia tốc hướng tâm, chúng ta cần hiểu rõ các công thức cơ bản và phương pháp tính toán liên quan. Dưới đây là các bước cơ bản và công thức cần sử dụng:

1. Công Thức Tính Lực Hướng Tâm

Lực hướng tâm (F_ht) là lực giữ cho một vật chuyển động theo quỹ đạo tròn đều, luôn hướng vào tâm của quỹ đạo đó. Công thức tính lực hướng tâm được cho bởi:

\[
F_{ht} = \frac{m \cdot v^2}{r}
\]

Trong đó:

• m là khối lượng của vật (kg).
• v là vận tốc của vật (m/s).
• r là bán kính quỹ đạo tròn (m).

2. Công Thức Tính Gia Tốc Hướng Tâm

Gia tốc hướng tâm (a_ht) là gia tốc cần thiết để thay đổi hướng của vận tốc khi vật chuyển động theo quỹ đạo tròn đều. Công thức tính gia tốc hướng tâm là:

\[
a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r
\]

Trong đó:

• v là vận tốc tuyến tính của vật (m/s).
• r là bán kính quỹ đạo tròn (m).
• \omega là tốc độ góc (rad/s).

3. Phương Pháp Tính Toán

1. Xác định các đại lượng đã biết: Đầu tiên, cần xác định khối lượng của vật, bán kính của quỹ đạo, và vận tốc của vật (hoặc tốc độ góc).
2. Áp dụng công thức: Sử dụng các công thức trên để tính toán lực hướng tâm và gia tốc hướng tâm dựa trên các đại lượng đã biết.
3. Kiểm tra đơn vị: Sau khi tính toán, đảm bảo rằng kết quả có đơn vị đúng để tránh sai sót.
4. Phân tích kết quả: Dựa trên kết quả thu được, phân tích ý nghĩa vật lý của lực và gia tốc hướng tâm đối với chuyển động của vật.

Với phương pháp tính toán từng bước như trên, việc giải quyết các bài toán liên quan đến lực hướng tâm và gia tốc hướng tâm trở nên rõ ràng và dễ dàng hơn.

1. Bài Tập Tự Luận về Lực Hướng Tâm

Dưới đây là một số bài tập tự luận về lực hướng tâm mà bạn cần làm để hiểu rõ hơn về khái niệm này:

• Bài 1: Một xe ô tô có khối lượng 1000 kg di chuyển trên một đường cong bán kính 50 m với vận tốc 20 m/s. Tính lực hướng tâm tác dụng lên xe.
• Bài 2: Một vệ tinh quay quanh Trái Đất với vận tốc không đổi theo quỹ đạo tròn. Cho biết vệ tinh có khối lượng 2000 kg và khoảng cách từ vệ tinh đến tâm Trái Đất là 6.6 × 10⁶ m. Hãy tính lực hướng tâm tác dụng lên vệ tinh.

2. Bài Tập Tính Toán Gia Tốc Hướng Tâm

Các bài tập sau đây sẽ giúp bạn nắm vững công thức và cách tính gia tốc hướng tâm:

• Bài 1: Tính gia tốc hướng tâm của một điểm trên vành ngoài của một bánh xe có bán kính 0.5 m quay với tốc độ 10 vòng/phút.
• Bài 2: Một viên bi quay tròn trong không khí với bán kính quỹ đạo là 0.2 m và tốc độ góc 5 rad/s. Hãy tính gia tốc hướng tâm của viên bi.

3. Lời Giải Chi Tiết và Phân Tích Bài Tập

Dưới đây là lời giải chi tiết và phân tích các bài tập để bạn tham khảo:

1. Lời giải Bài 1:

   Ta có công thức tính lực hướng tâm:
   
   F_{ht} = \frac{m \times v^2}{r}
   .
   Với m = 1000 kg, v = 20 m/s, và r = 50 m, thay vào công thức ta được:

   
   
   F_{ht} = \frac{1000 \times 20^2}{50} = 8000 \, \text{N}
   .

   Vậy, lực hướng tâm tác dụng lên xe là 8000 N.

2. Lời giải Bài 2:

   Dùng công thức tương tự, với m = 2000 kg, r = 6.6 \times 10^6 m, và v được tính từ tốc độ góc, ta có:
   
   F_{ht} = \frac{2000 \times v^2}{6.6 \times 10^6}
   .

   
   Khi v là tốc độ góc, công thức liên hệ giữa chu kỳ và tốc độ góc là:
   
   v = \frac{2 \pi r}{T}
   .
   Thay vào công thức trên để tính toán lực hướng tâm.

Trong chương học về Lực Hướng Tâm và Gia Tốc Hướng Tâm, chúng ta đã khám phá cách mà các lực này hoạt động trong các chuyển động tròn đều. Đây là những khái niệm cơ bản trong vật lý, nhưng lại có ứng dụng rộng rãi và quan trọng trong cả lý thuyết lẫn thực tiễn.

1. Tầm Quan Trọng của Lực Hướng Tâm và Gia Tốc Hướng Tâm

• Lực hướng tâm là lực cần thiết để duy trì chuyển động tròn đều, giữ cho vật di chuyển trên quỹ đạo nhất định.
• Gia tốc hướng tâm chính là hệ quả trực tiếp của lực hướng tâm, xác định độ thay đổi hướng của vận tốc khi vật di chuyển trên quỹ đạo.

2. Ứng Dụng Trong Các Hệ Thống Cơ Khí và Thiên Văn Học

Các khái niệm về lực hướng tâm và gia tốc hướng tâm có rất nhiều ứng dụng trong thực tiễn:

• Trong cơ khí, lực hướng tâm được sử dụng trong thiết kế các hệ thống truyền động, như bánh răng hay dây đai, giúp duy trì sự ổn định của chuyển động tròn.
• Trong thiên văn học, lực hấp dẫn giữa các hành tinh và vệ tinh hoạt động như một lực hướng tâm, giữ cho chúng di chuyển trên quỹ đạo quanh ngôi sao trung tâm.

3. Những Điểm Cần Lưu Ý Khi Giải Bài Tập Về Lực Hướng Tâm

Khi giải các bài tập về lực hướng tâm, cần lưu ý:

1. Xác định đúng các lực tác dụng và hướng của chúng để tính toán chính xác lực hướng tâm.
2. Áp dụng đúng công thức tính toán lực hướng tâm và gia tốc hướng tâm.
3. Sử dụng các công thức tính toán một cách linh hoạt, tùy theo tình huống cụ thể của bài toán.

Với những kiến thức và ứng dụng thực tiễn đã học, học sinh sẽ không chỉ nắm vững lý thuyết mà còn biết cách áp dụng vào các tình huống thực tế, từ đó hiểu sâu hơn về các hiện tượng tự nhiên và các nguyên lý khoa học.