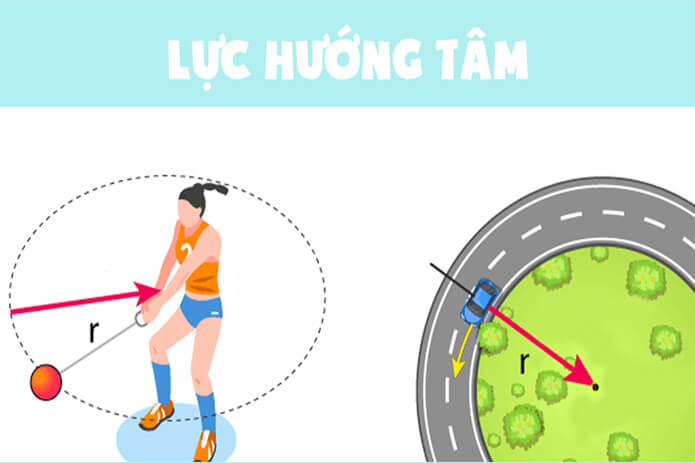
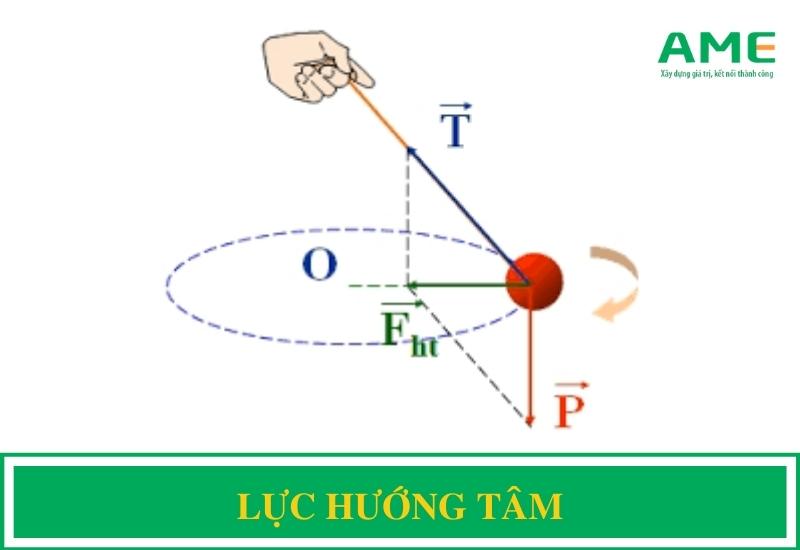
Chủ đề gia tốc hướng tâm lực hướng tâm: Gia tốc hướng tâm và lực hướng tâm là hai khái niệm quan trọng trong vật lý, giúp giải thích cách các vật thể chuyển động trên quỹ đạo tròn. Trong bài viết này, chúng ta sẽ khám phá chi tiết các công thức tính toán, ứng dụng thực tế và các ví dụ minh họa sinh động, giúp bạn nắm bắt rõ hơn về bản chất của hai hiện tượng này.
Mục lục
Gia Tốc Hướng Tâm và Lực Hướng Tâm
Trong lĩnh vực vật lý, đặc biệt là khi nghiên cứu về chuyển động tròn đều, hai khái niệm quan trọng cần phải hiểu rõ là gia tốc hướng tâm và lực hướng tâm. Đây là những yếu tố then chốt trong việc phân tích và giải thích các hiện tượng liên quan đến chuyển động tròn.
Gia Tốc Hướng Tâm
Gia tốc hướng tâm là gia tốc của một vật chuyển động tròn đều hướng vào tâm của quỹ đạo. Nó được gây ra bởi lực hướng tâm và có độ lớn được tính theo công thức:
Trong đó:
- a_{ht}: Gia tốc hướng tâm (m/s²)
- v: Tốc độ dài của vật (m/s)
- R: Bán kính của quỹ đạo tròn (m)
Lực Hướng Tâm
Lực hướng tâm là lực hoặc hợp lực tác dụng vào một vật đang chuyển động tròn đều, gây ra cho vật gia tốc hướng tâm. Lực này luôn hướng vào tâm của quỹ đạo và được tính bằng công thức:
Trong đó:
- F_{ht}: Lực hướng tâm (N)
- m: Khối lượng của vật (kg)
Ví Dụ Minh Họa
- Một vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất với bán kính quỹ đạo 7.000 km và tốc độ 7,57 km/s. Lực hướng tâm giữ vệ tinh trong quỹ đạo chính là lực hấp dẫn giữa Trái Đất và vệ tinh.
- Khi quay một viên đá buộc vào sợi dây theo quỹ đạo tròn, lực căng trong dây chính là lực hướng tâm giữ viên đá di chuyển trong quỹ đạo.
Ứng Dụng Trong Thực Tế
Các khái niệm về gia tốc và lực hướng tâm có nhiều ứng dụng thực tế, từ việc thiết kế các thiết bị quay ly tâm như máy giặt, đến việc phân tích chuyển động của các hành tinh trong hệ mặt trời. Hiểu rõ các khái niệm này giúp giải quyết nhiều vấn đề trong khoa học và kỹ thuật một cách hiệu quả.
.png)
1. Khái Niệm và Định Nghĩa
Trong chuyển động tròn đều, hai khái niệm thường được đề cập là gia tốc hướng tâm và lực hướng tâm. Để hiểu rõ hơn về các hiện tượng này, chúng ta hãy cùng đi vào định nghĩa chi tiết của từng khái niệm.
1.1 Gia Tốc Hướng Tâm
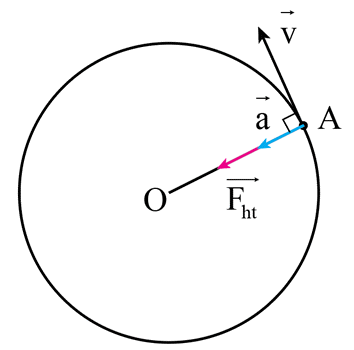
Gia tốc hướng tâm là loại gia tốc làm thay đổi hướng của vận tốc, giúp vật thể tiếp tục chuyển động theo một quỹ đạo tròn. Gia tốc này luôn hướng về tâm của quỹ đạo. Công thức tính gia tốc hướng tâm được thể hiện như sau:
Trong đó:
- a: Gia tốc hướng tâm (m/s2)
- v: Vận tốc tuyến tính của vật thể (m/s)
- r: Bán kính của quỹ đạo tròn (m)
1.2 Lực Hướng Tâm
Lực hướng tâm là lực cần thiết để duy trì một vật thể chuyển động trên quỹ đạo tròn đều. Lực này cũng luôn hướng về tâm của quỹ đạo, giúp vật thể không bị văng ra ngoài do quán tính. Công thức tính lực hướng tâm như sau:
Trong đó:
- F: Lực hướng tâm (N)
- m: Khối lượng của vật thể (kg)
- a: Gia tốc hướng tâm (m/s2)
- v: Vận tốc tuyến tính của vật thể (m/s)
- r: Bán kính của quỹ đạo tròn (m)
| Khái Niệm | Đặc Điểm |
|---|---|
| Gia Tốc Hướng Tâm |
|
| Lực Hướng Tâm |
|
Qua các định nghĩa và công thức trên, ta có thể thấy rằng gia tốc hướng tâm và lực hướng tâm có mối quan hệ chặt chẽ với nhau, đóng vai trò quan trọng trong việc duy trì chuyển động tròn đều của các vật thể.
2. Công Thức Tính Toán
Gia tốc hướng tâm và lực hướng tâm là hai khái niệm cơ bản trong chuyển động tròn đều, và công thức tính toán cho các đại lượng này giúp chúng ta hiểu rõ hơn về các lực tương tác trong các hệ thống chuyển động.
2.1 Công Thức Gia Tốc Hướng Tâm
Gia tốc hướng tâm (\(a\)) được xác định bởi công thức sau:
Trong đó:
- a: Gia tốc hướng tâm (m/s2)
- v: Vận tốc tuyến tính của vật thể (m/s)
- r: Bán kính của quỹ đạo tròn (m)
- \(\omega\): Vận tốc góc của vật thể (rad/s)
Gia tốc hướng tâm có thể được tính thông qua vận tốc tuyến tính hoặc vận tốc góc, tùy thuộc vào thông tin có sẵn của bài toán. Điều này cho phép linh hoạt trong việc giải quyết các bài toán liên quan đến chuyển động tròn.
2.2 Công Thức Lực Hướng Tâm
Lực hướng tâm (\(F\)) là lực cần thiết để giữ vật thể chuyển động theo quỹ đạo tròn, được tính bằng công thức:
Trong đó:
- F: Lực hướng tâm (N)
- m: Khối lượng của vật thể (kg)
- a: Gia tốc hướng tâm (m/s2)
- v: Vận tốc tuyến tính của vật thể (m/s)
- \(\omega\): Vận tốc góc của vật thể (rad/s)
- r: Bán kính của quỹ đạo tròn (m)
Lực hướng tâm là kết quả của các lực khác, ví dụ như lực hấp dẫn, lực ma sát hoặc lực căng dây, tác động lên vật thể, giữ cho nó di chuyển trên quỹ đạo tròn.
| Công Thức | Diễn Giải |
|---|---|
| \(a = \frac{v^2}{r}\) | Gia tốc hướng tâm dựa trên vận tốc tuyến tính và bán kính |
| \(a = \omega^2 \cdot r\) | Gia tốc hướng tâm dựa trên vận tốc góc và bán kính |
| \(F = \frac{m \cdot v^2}{r}\) | Lực hướng tâm dựa trên khối lượng, vận tốc tuyến tính và bán kính |
| \(F = m \cdot \omega^2 \cdot r\) | Lực hướng tâm dựa trên khối lượng, vận tốc góc và bán kính |
Các công thức trên không chỉ giúp chúng ta tính toán các giá trị cần thiết mà còn cung cấp cái nhìn tổng quát về mối quan hệ giữa các yếu tố trong chuyển động tròn. Hiểu rõ công thức tính toán sẽ giúp ta áp dụng hiệu quả trong các trường hợp thực tế và các bài tập vật lý.

3. Ví Dụ Minh Họa Thực Tế
Để hiểu rõ hơn về ứng dụng của gia tốc hướng tâm và lực hướng tâm, chúng ta sẽ xem xét một số ví dụ minh họa thực tế trong các lĩnh vực khác nhau, từ công nghệ không gian đến các phương tiện giao thông.
3.1 Vệ Tinh Nhân Tạo
Vệ tinh nhân tạo được phóng vào không gian để quay quanh Trái Đất theo quỹ đạo tròn hoặc elip. Trong trường hợp này, lực hấp dẫn của Trái Đất đóng vai trò là lực hướng tâm, giữ cho vệ tinh không bị văng ra khỏi quỹ đạo của nó. Cụ thể:
- Khối lượng vệ tinh: 1000 kg
- Bán kính quỹ đạo: 7000 km
- Vận tốc: 7500 m/s
Từ công thức lực hướng tâm:
Chúng ta tính được lực hướng tâm cần thiết:
3.2 Chuyển Động Tròn Đều của Ô Tô Trên Đường Cong
Một chiếc ô tô chạy trên đường cong với vận tốc không đổi cũng là một ví dụ điển hình về lực hướng tâm. Lực ma sát giữa lốp xe và mặt đường cung cấp lực hướng tâm cần thiết để xe di chuyển theo đường cong. Giả sử:
- Khối lượng ô tô: 1500 kg
- Bán kính đường cong: 50 m
- Vận tốc: 20 m/s
Áp dụng công thức lực hướng tâm, ta có:
Do đó, lực ma sát giữa bánh xe và mặt đường phải đủ để tạo ra lực hướng tâm 12 kN để giữ cho xe di chuyển an toàn trên đường cong.
3.3 Các Trò Chơi Giải Trí tại Công Viên
Trong các trò chơi giải trí như vòng quay ngựa gỗ, tàu lượn siêu tốc, lực hướng tâm cũng đóng vai trò quan trọng. Những trò chơi này được thiết kế để đảm bảo an toàn cho người chơi bằng cách tính toán lực hướng tâm cần thiết, ngăn không cho họ bị văng ra ngoài. Ví dụ:
- Vòng quay ngựa gỗ: Có vận tốc góc 0.5 rad/s, bán kính 5 m
Gia tốc hướng tâm của mỗi con ngựa gỗ là:
| Ví Dụ | Gia Tốc Hướng Tâm | Lực Hướng Tâm |
|---|---|---|
| Vệ tinh nhân tạo | N/A | 8.04 kN |
| Ô tô trên đường cong | N/A | 12 kN |
| Vòng quay ngựa gỗ | 1.25 m/s2 | N/A |
Các ví dụ trên minh họa sự hiện diện và vai trò quan trọng của gia tốc hướng tâm và lực hướng tâm trong nhiều hoạt động hàng ngày và công nghệ cao, giúp chúng ta hiểu rõ hơn về các nguyên tắc vật lý cơ bản trong cuộc sống.

4. Ứng Dụng Trong Thực Tế
Gia tốc hướng tâm và lực hướng tâm có nhiều ứng dụng quan trọng trong đời sống và công nghệ. Những ứng dụng này giúp cải thiện hiệu quả và sự an toàn trong nhiều lĩnh vực khác nhau.
4.1 Trong Khoa Học và Kỹ Thuật
- Thiết kế và vận hành tàu vũ trụ: Lực hướng tâm là yếu tố chính trong việc tính toán quỹ đạo của các tàu vũ trụ và vệ tinh. Bằng cách điều chỉnh lực đẩy và vận tốc của tàu, các nhà khoa học có thể đảm bảo rằng các thiết bị này quay quanh Trái Đất theo quỹ đạo mong muốn mà không bị rơi xuống hoặc bay ra khỏi không gian.
- Máy ly tâm: Trong các phòng thí nghiệm, máy ly tâm sử dụng gia tốc hướng tâm để tách các chất khác nhau trong hỗn hợp dựa trên khối lượng riêng. Bằng cách quay với tốc độ cao, các thành phần nặng hơn bị đẩy ra xa trục quay hơn các thành phần nhẹ hơn, giúp tách biệt chúng.
- Các công trình xây dựng: Lực hướng tâm được xem xét khi thiết kế các công trình có hình dạng vòng tròn hoặc xoắn ốc như cầu vượt, đường hầm, và các tòa nhà cao tầng để đảm bảo sự ổn định và an toàn trong quá trình sử dụng.
4.2 Trong Thiết Bị Hàng Ngày
- Xe cộ: Hệ thống treo và bánh xe của ô tô được thiết kế để tạo ra lực hướng tâm, giữ cho xe ổn định khi di chuyển trên các đoạn đường cong. Điều này không chỉ giúp tăng tính an toàn mà còn cải thiện trải nghiệm lái xe.
- Máy giặt: Trong chế độ vắt, lồng giặt của máy quay với tốc độ cao tạo ra lực hướng tâm. Lực này đẩy nước ra khỏi quần áo, giúp chúng khô nhanh hơn.
- Các thiết bị trò chơi: Trong các trò chơi như vòng quay ngựa gỗ hay đu quay, lực hướng tâm được sử dụng để giữ người chơi an toàn trong khi thiết bị quay. Các lực này được tính toán cẩn thận để đảm bảo rằng người chơi không bị văng ra ngoài.
| Lĩnh Vực | Ứng Dụng | Lợi Ích |
|---|---|---|
| Khoa học vũ trụ | Quỹ đạo vệ tinh, tàu vũ trụ | Đảm bảo hoạt động ổn định, chính xác |
| Y học, hóa học | Máy ly tâm | Tách chiết, phân loại chất hiệu quả |
| Giao thông | Hệ thống treo xe, đường cong | Tăng cường an toàn, ổn định khi di chuyển |
| Gia dụng | Máy giặt, thiết bị trò chơi | Tiện ích, an toàn cho người dùng |
Các ứng dụng của gia tốc hướng tâm và lực hướng tâm trong thực tế không chỉ giới hạn trong các lĩnh vực khoa học và công nghệ cao mà còn hiện diện trong nhiều khía cạnh của đời sống hàng ngày, giúp nâng cao chất lượng và hiệu quả trong hoạt động của con người.

5. Kiến Thức Mở Rộng
Để hiểu rõ hơn về gia tốc hướng tâm và lực hướng tâm, chúng ta cần tìm hiểu thêm một số khái niệm liên quan cũng như các hiện tượng vật lý khác có liên quan đến chúng. Dưới đây là một số kiến thức mở rộng giúp chúng ta có cái nhìn toàn diện hơn về các lực này trong vật lý.
5.1 Chuyển Động Li Tâm
Chuyển động li tâm xảy ra khi một vật thể di chuyển ra xa trục quay do tác động của gia tốc li tâm. Gia tốc li tâm được định nghĩa là gia tốc hướng ra xa từ tâm của vòng quay và có giá trị bằng:
Gia tốc li tâm thường gây ra hiệu ứng cảm nhận rằng vật thể đang bị đẩy ra khỏi trục quay. Hiện tượng này được thấy rõ ràng trong các thiết bị như máy ly tâm và trong các trò chơi như đu quay.
5.2 Lực Hấp Dẫn và Chuyển Động Quỹ Đạo
Lực hấp dẫn đóng vai trò quan trọng trong việc giữ các vật thể trong quỹ đạo. Lực này hoạt động như một lực hướng tâm, giữ các hành tinh, mặt trăng và vệ tinh quay quanh các thiên thể lớn hơn. Công thức tính lực hấp dẫn giữa hai vật thể là:
Trong đó:
- G: Hằng số hấp dẫn (6.674×10−11 N(m/kg)2)
- m1 và m2: Khối lượng của hai vật thể (kg)
- r: Khoảng cách giữa tâm của hai vật thể (m)
Hiểu về lực hấp dẫn giúp chúng ta giải thích nhiều hiện tượng thiên văn như sự hình thành quỹ đạo của các hành tinh và chuyển động của các thiên thạch.
5.3 Lực Coriolis
Lực Coriolis là một lực quán tính được tạo ra bởi sự quay của Trái Đất, ảnh hưởng đến chuyển động của các vật thể trên bề mặt. Lực này làm cho các vật thể chuyển động lệch hướng so với đường thẳng ban đầu, thường thấy trong dòng chảy của gió và nước biển. Công thức của lực Coriolis là:
Trong đó:
- m: Khối lượng của vật thể (kg)
- v: Vận tốc của vật thể (m/s)
- \(\Omega\): Vận tốc góc của Trái Đất (rad/s)
Lực Coriolis ảnh hưởng đáng kể đến khí hậu và môi trường, góp phần vào việc hình thành các cơn bão và dòng hải lưu.
5.4 Tác Động của Lực Hướng Tâm trong Vật Lý Hạt Nhân
Trong vật lý hạt nhân, lực hướng tâm có thể ảnh hưởng đến chuyển động của các hạt dưới mức nguyên tử trong các gia tốc hạt nhân. Các hạt được gia tốc trong một vòng tròn hoặc quỹ đạo hình elip nhờ lực điện từ, và lực hướng tâm cần thiết được cung cấp bởi trường điện từ mạnh.
| Chủ Đề | Mô Tả | Ứng Dụng |
|---|---|---|
| Chuyển động li tâm | Gia tốc hướng ra ngoài từ tâm quay | Máy ly tâm, đu quay |
| Lực hấp dẫn | Lực hút giữa hai vật thể có khối lượng | Quỹ đạo hành tinh, mặt trăng |
| Lực Coriolis | Lực quán tính do sự quay của Trái Đất | Khí hậu, dòng chảy đại dương |
| Vật lý hạt nhân | Gia tốc hạt nhân trong trường điện từ | Máy gia tốc hạt |
Những kiến thức mở rộng về gia tốc hướng tâm và lực hướng tâm giúp chúng ta hiểu sâu hơn về các hiện tượng vật lý và cách chúng ứng dụng trong thực tế, từ các thí nghiệm khoa học đến đời sống hàng ngày.
XEM THÊM:
6. Câu Hỏi Thường Gặp
Dưới đây là một số câu hỏi thường gặp liên quan đến gia tốc hướng tâm và lực hướng tâm. Những giải đáp này sẽ giúp bạn hiểu rõ hơn về các khái niệm và ứng dụng của chúng trong thực tế.
6.1 Gia Tốc Hướng Tâm và Lực Hướng Tâm Khác Nhau Như Thế Nào?
- Gia tốc hướng tâm là sự thay đổi vận tốc của một vật thể theo hướng về tâm của đường tròn mà nó đang di chuyển. Nó luôn hướng vào trung tâm của đường tròn và được tính theo công thức:
$$ a = \frac{v^2}{r} $$
trong đó:
- a: Gia tốc hướng tâm (m/s2)
- v: Vận tốc của vật thể (m/s)
- r: Bán kính của đường tròn (m)
- Lực hướng tâm là lực cần thiết để duy trì một vật thể di chuyển theo một đường tròn và cũng luôn hướng về tâm của đường tròn. Lực hướng tâm được tính theo công thức:
$$ F = m \cdot a $$
hoặc
$$ F = m \cdot \frac{v^2}{r} $$
trong đó:
- F: Lực hướng tâm (N)
- m: Khối lượng của vật thể (kg)
- a: Gia tốc hướng tâm (m/s2)
6.2 Lực Hướng Tâm Có Phải Là Một Loại Lực Độc Lập Không?
Không, lực hướng tâm không phải là một loại lực độc lập. Nó là một kết quả của sự tác động của các lực khác như lực ma sát, lực hấp dẫn, hay lực căng của dây... Ví dụ:
- Trong trường hợp ô tô quay vòng, lực ma sát giữa lốp xe và mặt đường đóng vai trò là lực hướng tâm, giúp xe di chuyển theo đường tròn.
- Trong chuyển động của các hành tinh quanh Mặt Trời, lực hấp dẫn giữa hành tinh và Mặt Trời tạo ra lực hướng tâm.
- Trong trò chơi đu quay, lực căng của dây xích hoặc thanh nối chính là lực hướng tâm giữ cho người chơi di chuyển theo quỹ đạo tròn.
6.3 Tại Sao Lực Hướng Tâm Luôn Hướng Về Tâm Của Đường Tròn?
Lực hướng tâm luôn hướng về tâm của đường tròn bởi vì nó là lực cần thiết để thay đổi hướng của vận tốc của vật thể, giữ cho vật thể di chuyển theo quỹ đạo tròn. Nếu không có lực này, vật thể sẽ tiếp tục di chuyển theo đường thẳng do quán tính (theo định luật thứ nhất của Newton).
6.4 Lực Ly Tâm Có Phải Là Một Loại Lực Thật Không?
Lực ly tâm thực chất là một lực giả, cảm nhận được khi một vật thể di chuyển trong một hệ quy chiếu quay. Khi một vật thể di chuyển trong một hệ quy chiếu quay, quán tính của vật tạo ra cảm giác như có một lực đẩy nó ra khỏi tâm quay. Tuy nhiên, lực này không thực sự tồn tại theo nghĩa vật lý, mà chỉ là kết quả của quán tính.
6.5 Gia Tốc Hướng Tâm Có Ảnh Hưởng Như Thế Nào Đến Vật Thể Chuyển Động?
Gia tốc hướng tâm ảnh hưởng đến vật thể chuyển động bằng cách thay đổi hướng của vận tốc mà không thay đổi độ lớn của nó. Điều này làm cho vật thể duy trì chuyển động theo một quỹ đạo tròn. Nếu gia tốc hướng tâm không đủ, vật thể sẽ di chuyển ra khỏi quỹ đạo tròn và đi theo một đường thẳng do quán tính.
6.6 Làm Thế Nào Để Tăng Lực Hướng Tâm?
Để tăng lực hướng tâm, bạn có thể:
- Tăng khối lượng của vật thể (m)
- Tăng vận tốc của vật thể (v)
- Giảm bán kính của đường tròn (r)
Các biện pháp này sẽ làm tăng lực hướng tâm theo công thức \( F = m \cdot \frac{v^2}{r} \), từ đó giúp duy trì chuyển động tròn của vật thể hiệu quả hơn.