Chủ đề đẳng tích: Đẳng tích là một khái niệm quan trọng trong Vật lý, đặc biệt liên quan đến định luật Sác-lơ. Bài viết này sẽ giúp bạn nắm vững bản chất của quá trình đẳng tích, ứng dụng trong thực tế, và cung cấp các bài tập minh họa chi tiết. Khám phá sâu hơn về hiện tượng này để áp dụng vào học tập và đời sống hàng ngày.
Mục lục
Quá Trình Đẳng Tích và Ứng Dụng
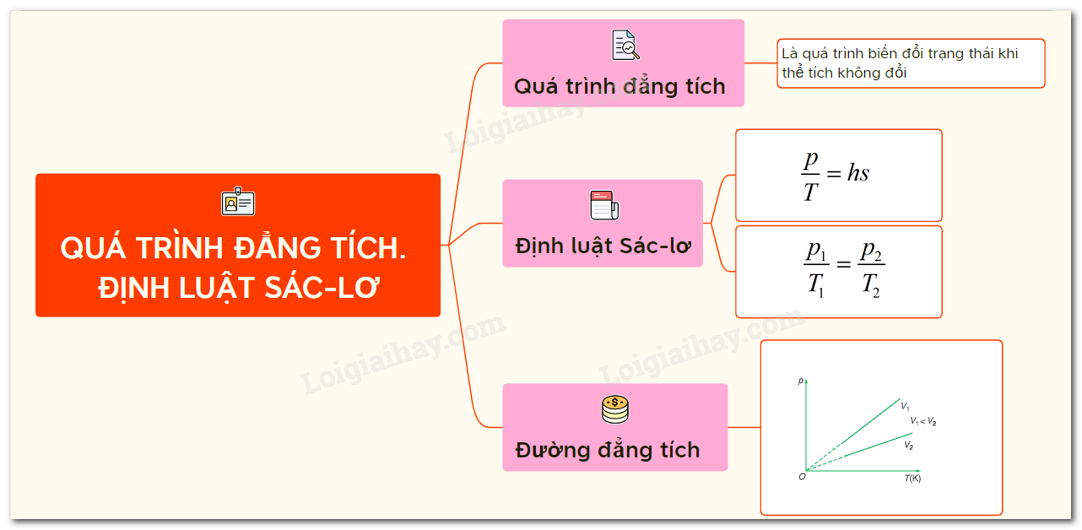
Quá trình đẳng tích là quá trình biến đổi trạng thái của một lượng khí khi thể tích được giữ không đổi. Trong quá trình này, sự thay đổi nhiệt độ sẽ dẫn đến sự thay đổi áp suất, theo đúng định luật Sác-lơ.
1. Định Luật Sác-lơ
Định luật Sác-lơ phát biểu rằng trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối. Công thức được viết như sau:
$$ \frac{p_1}{T_1} = \frac{p_2}{T_2} $$
Trong đó:
- \(p_1, T_1\): Áp suất và nhiệt độ tuyệt đối ở trạng thái ban đầu.
- \(p_2, T_2\): Áp suất và nhiệt độ tuyệt đối ở trạng thái cuối.
2. Đường Đẳng Tích
Đường đẳng tích là đường biểu diễn sự biến thiên của áp suất theo nhiệt độ khi thể tích không đổi. Trong hệ tọa độ \((p,T)\), đường đẳng tích là một đường thẳng đi qua gốc tọa độ.
3. Ứng Dụng Thực Tế
- Động cơ đốt trong: Trong chu trình Otto, phần quá trình đẳng tích diễn ra khi nhiệt độ tăng nhanh, dẫn đến tăng áp suất.
- Nồi áp suất: Khi sử dụng nồi áp suất, thể tích bên trong không thay đổi, nhưng nhiệt độ và áp suất tăng lên khi nấu.
- HVAC: Các hệ thống sưởi, thông gió và điều hòa không khí sử dụng nguyên lý đẳng tích để điều chỉnh áp suất và nhiệt độ khí trong quá trình hoạt động.
4. Bài Tập Vận Dụng
Dưới đây là một ví dụ bài tập vận dụng định luật Sác-lơ trong quá trình đẳng tích:
Ví dụ: Một lượng khí ở áp suất \(p_1 = 2 atm\) và nhiệt độ \(T_1 = 300 K\). Khi nhiệt độ tăng lên \(T_2 = 600 K\) trong quá trình đẳng tích, hãy tính áp suất cuối cùng \(p_2\).
Giải:
Áp dụng định luật Sác-lơ:
$$ \frac{p_1}{T_1} = \frac{p_2}{T_2} $$
Suy ra:
$$ p_2 = \frac{p_1 \cdot T_2}{T_1} = \frac{2 \cdot 600}{300} = 4 atm $$
Vậy, áp suất cuối cùng là \(p_2 = 4 atm\).
.png)
I. Giới thiệu về quá trình đẳng tích
Quá trình đẳng tích là một quá trình nhiệt động lực học đặc biệt, trong đó thể tích của một hệ kín được giữ nguyên không đổi. Trong quá trình này, chỉ có hai đại lượng là áp suất (P) và nhiệt độ (T) thay đổi. Quá trình đẳng tích thường được nghiên cứu trong các hệ thống chứa khí, như bình kín hoặc xi-lanh, nơi mà thể tích không thể thay đổi do các điều kiện vật lý.
Theo định luật Sác-lơ, trong quá trình đẳng tích, áp suất của một lượng khí cố định tỉ lệ thuận với nhiệt độ tuyệt đối của nó. Điều này có nghĩa là khi nhiệt độ tăng, áp suất cũng tăng theo, và ngược lại. Công thức mô tả mối quan hệ này là:
$$\frac{P}{T} = \text{hằng số}$$
Trong đó:
- P: Áp suất của khí
- T: Nhiệt độ tuyệt đối (đơn vị Kelvin)
Quá trình đẳng tích không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong cuộc sống, từ việc phân tích hoạt động của các động cơ nhiệt, cho đến nghiên cứu và thiết kế các hệ thống làm lạnh và điều hòa không khí. Việc hiểu rõ quá trình đẳng tích giúp nắm bắt sâu hơn về cơ học chất khí và nhiệt động lực học.
II. Định luật Sác-lơ
Định luật Sác-lơ là một trong những định luật cơ bản trong nhiệt động lực học, mô tả mối quan hệ giữa áp suất và nhiệt độ của một lượng khí trong quá trình đẳng tích, tức là khi thể tích được giữ cố định. Định luật này phát biểu rằng:
$$\frac{P}{T} = \text{hằng số}$$
Điều này có nghĩa là trong một hệ thống khí có thể tích không đổi, áp suất \( P \) của khí sẽ tỉ lệ thuận với nhiệt độ tuyệt đối \( T \). Cụ thể, khi nhiệt độ tăng, áp suất của khí cũng tăng, và ngược lại.
Chúng ta có thể biểu diễn định luật Sác-lơ dưới dạng hai trạng thái khác nhau của cùng một lượng khí:
$$\frac{P_1}{T_1} = \frac{P_2}{T_2}$$
Trong đó:
- P1: Áp suất ban đầu của khí
- T1: Nhiệt độ tuyệt đối ban đầu (Kelvin)
- P2: Áp suất sau khi thay đổi nhiệt độ
- T2: Nhiệt độ tuyệt đối sau khi thay đổi (Kelvin)
Định luật Sác-lơ không chỉ mang lại sự hiểu biết về mối quan hệ giữa áp suất và nhiệt độ trong điều kiện thể tích không đổi, mà còn là cơ sở cho nhiều ứng dụng thực tiễn. Chẳng hạn, nó được áp dụng trong việc tính toán và thiết kế các hệ thống điều hòa không khí, tủ lạnh, và động cơ đốt trong.
Để minh họa rõ ràng hơn, hãy xét một ví dụ: nếu một lượng khí trong xi-lanh có thể tích không đổi và nhiệt độ của nó tăng gấp đôi, theo định luật Sác-lơ, áp suất của khí này cũng sẽ tăng gấp đôi, điều này có thể gây ra áp lực lớn lên các bức tường của xi-lanh.

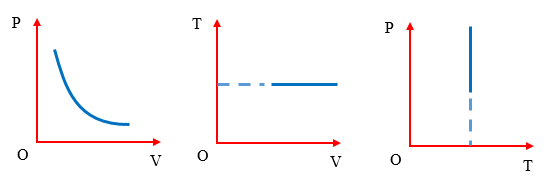
III. Đường đẳng tích
Đường đẳng tích là một khái niệm quan trọng trong nhiệt động lực học, đặc biệt khi phân tích các quá trình liên quan đến khí lý tưởng. Đây là đường biểu diễn mối quan hệ giữa áp suất và nhiệt độ của một lượng khí khi thể tích của nó được giữ cố định.
Trong hệ tọa độ áp suất - nhiệt độ (P-T), đường đẳng tích được biểu diễn dưới dạng một đường thẳng, nơi áp suất tỉ lệ thuận với nhiệt độ tuyệt đối. Điều này có nghĩa là khi nhiệt độ tăng, áp suất cũng tăng theo, miễn là thể tích không đổi. Phương trình của đường đẳng tích có thể được biểu diễn như sau:
$$ P = kT $$
Trong đó:
- P: Áp suất của khí
- T: Nhiệt độ tuyệt đối (Kelvin)
- k: Hằng số, phụ thuộc vào thể tích và số mol của khí
Đường đẳng tích thường bắt đầu từ gốc tọa độ trong hệ tọa độ P-T, tức là khi nhiệt độ bằng 0, áp suất cũng sẽ bằng 0 theo lý thuyết. Tuy nhiên, trên thực tế, không khí không thể đạt được nhiệt độ tuyệt đối (0 Kelvin), nên đường đẳng tích chỉ mang tính chất mô hình hóa.
Ví dụ, trong một hệ thống khí lý tưởng, khi nhiệt độ tăng gấp đôi, áp suất cũng sẽ tăng gấp đôi theo định luật Sác-lơ. Đường đẳng tích giúp các nhà vật lý và kỹ sư dễ dàng hình dung và tính toán sự biến đổi của các đại lượng khí trong điều kiện thể tích không đổi.
Những đường đẳng tích này không chỉ là lý thuyết mà còn được sử dụng thực tế trong việc thiết kế và phân tích các hệ thống nhiệt, như động cơ nhiệt, tủ lạnh, và các thiết bị điều hòa không khí, nơi mà việc kiểm soát áp suất và nhiệt độ là yếu tố then chốt.

IV. Bài tập và ví dụ về quá trình đẳng tích
Để nắm vững lý thuyết về quá trình đẳng tích, việc thực hành qua các bài tập và ví dụ minh họa là rất quan trọng. Dưới đây là một số bài tập và ví dụ giúp bạn hiểu rõ hơn về cách áp dụng định luật Sác-lơ và các khái niệm liên quan trong thực tế.
1. Bài tập tự luận về quá trình đẳng tích
Một bình chứa khí lý tưởng có thể tích không đổi. Khi nhiệt độ của khí trong bình tăng từ 300 K lên 600 K, hãy tính áp suất của khí sau khi nhiệt độ tăng biết rằng áp suất ban đầu là 2 atm.
Một lượng khí có thể tích không đổi được đun nóng từ 250 K lên 500 K. Biết áp suất ban đầu là 1.5 atm, tính áp suất sau khi nhiệt độ thay đổi.
Một khí lý tưởng được giữ trong một bình kín với thể tích không đổi. Áp suất ban đầu là 101.3 kPa ở nhiệt độ 273 K. Nếu nhiệt độ tăng lên 546 K, hãy xác định áp suất mới của khí.
2. Bài tập trắc nghiệm về quá trình đẳng tích
Trong một quá trình đẳng tích, nhiệt độ của khí tăng gấp ba lần. Áp suất của khí sẽ:
- Tăng gấp ba lần
- Giảm đi một nửa
- Không thay đổi
- Tăng gấp đôi
Định luật Sác-lơ phát biểu rằng, trong một quá trình đẳng tích, áp suất của khí tỉ lệ thuận với:
- Thể tích
- Nhiệt độ tuyệt đối
- Khối lượng
- Số mol khí
Đường đẳng tích trong hệ tọa độ P-T là một đường:
- Thẳng
- Cong
- Parabol
- Hyperbol
3. Ví dụ minh họa quá trình đẳng tích
Giả sử bạn có một xi-lanh chứa khí lý tưởng với thể tích không đổi. Nếu ban đầu áp suất của khí là 100 kPa ở nhiệt độ 300 K, khi nhiệt độ tăng lên 450 K, áp suất mới của khí sẽ là:
$$ P_2 = P_1 \cdot \frac{T_2}{T_1} = 100 \, \text{kPa} \cdot \frac{450 \, \text{K}}{300 \, \text{K}} = 150 \, \text{kPa} $$
Điều này minh họa rõ ràng định luật Sác-lơ và cho thấy cách áp suất của khí tăng khi nhiệt độ tăng trong điều kiện thể tích không đổi.