Chủ đề đồ thị đẳng tích: Đồ thị đẳng tích là một phần quan trọng trong lĩnh vực nhiệt động lực học, đặc biệt trong việc nghiên cứu các quá trình nhiệt trong hệ thống khí lý tưởng. Bài viết này sẽ cung cấp kiến thức tổng quan về khái niệm đồ thị đẳng tích, các ứng dụng phổ biến và phân tích chi tiết cách vẽ và hiểu đồ thị này. Hãy cùng tìm hiểu sâu hơn về nguyên tắc hoạt động của quá trình đẳng tích và vai trò của nó trong vật lý.
Mục lục
Đồ Thị Đẳng Tích Trong Nhiệt Động Lực Học
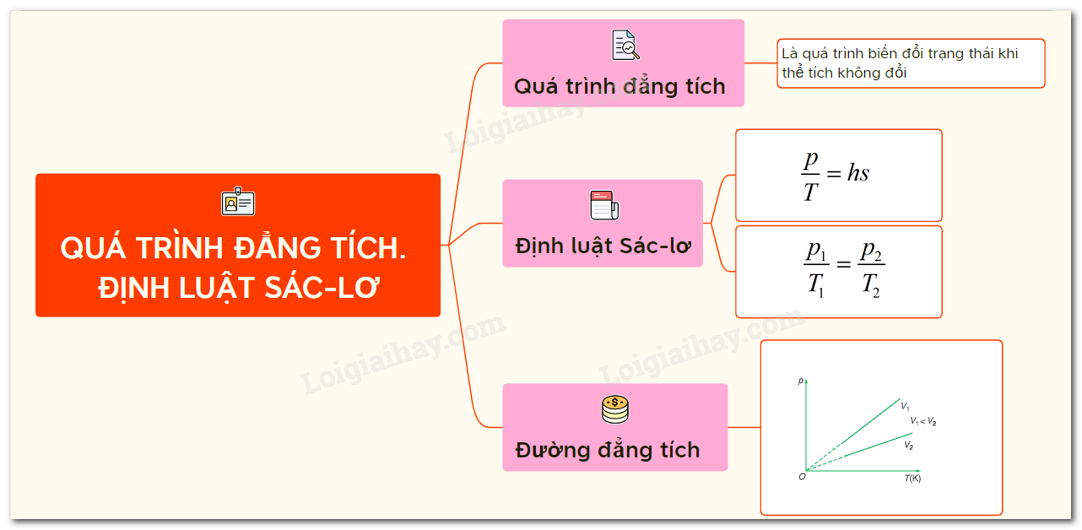
Quá trình đẳng tích là một quá trình nhiệt động lực học mà trong đó thể tích của hệ không thay đổi, dù các yếu tố khác như áp suất và nhiệt độ có thể biến đổi. Để hiểu rõ hơn về quá trình này, chúng ta sẽ đi vào chi tiết lý thuyết và ứng dụng thực tế thông qua định luật Sác-lơ.
1. Định Luật Sác-lơ Và Ứng Dụng
Định luật Sác-lơ mô tả mối quan hệ giữa áp suất và nhiệt độ của một lượng khí cố định khi thể tích không thay đổi. Định luật này phát biểu rằng áp suất của một lượng khí tỉ lệ thuận với nhiệt độ tuyệt đối của nó khi thể tích không đổi:
p ∝ T, hay \( \frac{p}{T} = \text{hằng số} \)
Phương trình trên biểu diễn rằng khi nhiệt độ tăng, áp suất cũng sẽ tăng theo và ngược lại. Điều này được thể hiện rõ ràng trên đồ thị đẳng tích, nơi áp suất được biểu diễn theo nhiệt độ với thể tích không đổi.
2. Đồ Thị Đẳng Tích
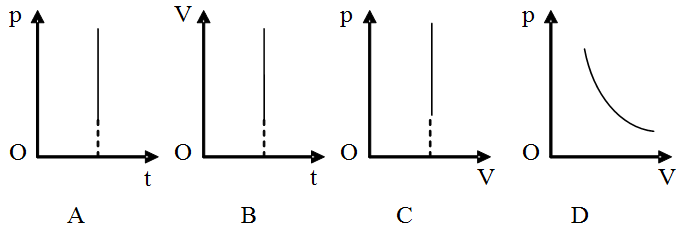
Đồ thị đẳng tích biểu diễn mối quan hệ giữa áp suất (p) và nhiệt độ (T) với thể tích không đổi. Trên đồ thị này, đường biểu diễn là một đường thẳng dốc lên, cho thấy áp suất tỉ lệ thuận với nhiệt độ:

Công thức của định luật Sác-lơ cho quá trình đẳng tích là:
\( \frac{p_1}{T_1} = \frac{p_2}{T_2} \)
3. Ứng Dụng Thực Tế
- Hệ thống làm lạnh: Định luật Sác-lơ được ứng dụng trong các hệ thống điều hòa không khí, nơi áp suất và nhiệt độ được kiểm soát để điều chỉnh luồng không khí.
- Đo nhiệt độ: Trong nhiều ngành công nghiệp và y tế, quá trình đo nhiệt độ dựa trên nguyên lý của định luật Sác-lơ để đảm bảo độ chính xác cao.
4. Ví Dụ Minh Họa
Giả sử một lượng khí có áp suất ban đầu là 1.20×105 Pa ở nhiệt độ 273K. Khi nhiệt độ tăng lên 303K, áp suất mới sẽ là:
\( p_2 = p_1 \times \frac{T_2}{T_1} = 1.20×10^{5} \times \frac{303}{273} = 1.33×10^{5} \, \text{Pa} \)
5. Kết Luận
Đồ thị đẳng tích là một trong những biểu đồ quan trọng trong nhiệt động lực học, giúp chúng ta hiểu rõ hơn về mối liên hệ giữa các đại lượng nhiệt động trong quá trình giữ thể tích không đổi. Các ứng dụng của định luật Sác-lơ không chỉ giới hạn trong lý thuyết mà còn xuất hiện rộng rãi trong cuộc sống hàng ngày, từ điều hòa không khí đến các quy trình sản xuất công nghiệp.
.png)
1. Giới Thiệu Về Quá Trình Đẳng Tích
Quá trình đẳng tích là một dạng biến đổi trạng thái đặc biệt trong nhiệt động học, xảy ra khi thể tích của hệ không thay đổi trong suốt quá trình. Khi thể tích không đổi, sự biến thiên của nhiệt độ sẽ dẫn đến thay đổi tương ứng trong áp suất của khí. Quá trình này được miêu tả bởi định luật Charles (Sác-lơ), cho rằng áp suất tỷ lệ thuận với nhiệt độ tuyệt đối trong điều kiện thể tích không đổi. Điều này được minh họa qua các thí nghiệm và đồ thị đẳng tích, biểu diễn mối quan hệ giữa áp suất và nhiệt độ.
- Quá trình đẳng tích thường được ứng dụng trong các bài toán nhiệt động học liên quan đến khí lý tưởng.
- Định luật Sác-lơ: \( \frac{p_1}{T_1} = \frac{p_2}{T_2} \), trong đó \( p \) là áp suất và \( T \) là nhiệt độ tuyệt đối.
- Đường đẳng tích trên đồ thị có hình dạng là một đường thẳng biểu diễn sự phụ thuộc của áp suất vào nhiệt độ khi thể tích không đổi.
3. Ứng Dụng Thực Tiễn Của Quá Trình Đẳng Tích
Quá trình đẳng tích có nhiều ứng dụng thực tiễn quan trọng trong lĩnh vực nhiệt động học và kỹ thuật. Một trong những ứng dụng điển hình là trong hoạt động của động cơ đốt trong. Khi hỗn hợp không khí và nhiên liệu bị nén trong xilanh mà thể tích không thay đổi, sự gia nhiệt sẽ làm tăng áp suất, giúp động cơ hoạt động hiệu quả hơn. Điều này phản ánh nguyên lý cơ bản của quá trình đẳng tích.
- Trong các nghiên cứu khoa học, quá trình đẳng tích được sử dụng để hiểu rõ hơn về các tính chất của khí lý tưởng, từ đó ứng dụng vào các mô hình nhiệt động học.
- Hệ thống điều hòa không khí và tủ lạnh cũng sử dụng nguyên lý đẳng tích trong quá trình chuyển đổi nhiệt độ, giúp kiểm soát và duy trì môi trường nhiệt độ ổn định.
- Các thí nghiệm trong phòng thí nghiệm liên quan đến khí lý tưởng thường dựa trên quá trình đẳng tích để xác định hằng số khí và các thuộc tính vật lý khác.
Những ứng dụng này cho thấy quá trình đẳng tích không chỉ là một khái niệm lý thuyết mà còn mang giá trị thực tiễn cao, đóng góp vào nhiều lĩnh vực trong đời sống và công nghệ.

4. Các Bài Tập Minh Họa
Dưới đây là một số bài tập minh họa về quá trình đẳng tích nhằm giúp bạn hiểu rõ hơn về mối quan hệ giữa áp suất và nhiệt độ khi thể tích không thay đổi:
- Bài tập 1: Một lượng khí lý tưởng có thể tích không đổi được nung nóng từ \( 300K \) lên \( 600K \). Hãy xác định sự thay đổi áp suất của khí.
- Bài tập 2: Một xilanh chứa khí có thể tích không đổi. Áp suất ban đầu là \( 2 \, atm \) ở nhiệt độ \( 27^\circ C \). Khi nhiệt độ tăng lên \( 127^\circ C \), tính áp suất cuối cùng của khí.
- Bài tập 3: Một quá trình đẳng tích xảy ra trong điều kiện nhiệt độ giảm từ \( 500K \) xuống \( 250K \). Tính phần trăm giảm áp suất.
Lời giải: Sử dụng phương trình trạng thái đẳng tích \( \frac{p_1}{T_1} = \frac{p_2}{T_2} \), ta có thể tính được:
\[
p_2 = p_1 \times \frac{T_2}{T_1} = p_1 \times \frac{600}{300} = 2p_1
\]
Lời giải: Chuyển đổi nhiệt độ sang Kelvin và áp dụng phương trình đẳng tích:
\[
p_2 = 2 \, atm \times \frac{400K}{300K} = \frac{8}{3} \, atm
\]
Lời giải: Áp suất cuối cùng giảm còn \( 50\% \) so với áp suất ban đầu, do đó phần trăm giảm là \( 50\% \).
Các bài tập này giúp bạn nắm bắt quy luật biến đổi áp suất và nhiệt độ trong quá trình đẳng tích, đồng thời rèn luyện kỹ năng áp dụng công thức vào thực tế.

XEM THÊM:
5. So Sánh Quá Trình Đẳng Tích Và Quá Trình Đẳng Nhiệt
Quá trình đẳng tích và quá trình đẳng nhiệt là hai khái niệm cơ bản trong nhiệt động học, mỗi quá trình có những đặc điểm và ứng dụng riêng biệt. Dưới đây là bảng so sánh chi tiết về hai quá trình này:
| Tiêu chí | Quá trình đẳng tích | Quá trình đẳng nhiệt |
|---|---|---|
| Định nghĩa | Quá trình diễn ra khi thể tích không đổi (V = const) và nhiệt độ hoặc áp suất thay đổi. | Quá trình diễn ra khi nhiệt độ không đổi (T = const) và thể tích hoặc áp suất thay đổi. |
| Phương trình trạng thái | \( \frac{p_1}{T_1} = \frac{p_2}{T_2} \) | \( pV = const \) |
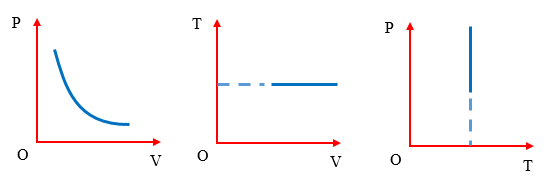
| Đặc điểm đồ thị | Đồ thị trong mặt phẳng \( p - T \) là đường thẳng đi qua gốc tọa độ. | Đồ thị trong mặt phẳng \( p - V \) là đường hyperbol. |
| Ứng dụng thực tiễn | Thường gặp trong các quá trình như nén khí trong xilanh khi không thay đổi thể tích. | Ứng dụng trong động cơ nhiệt, nơi cần giữ nhiệt độ ổn định. |
Nhìn chung, sự khác biệt chính giữa hai quá trình này nằm ở yếu tố nào được giữ cố định. Hiểu rõ sự khác biệt này sẽ giúp bạn áp dụng chúng hiệu quả trong các bài toán nhiệt động học.

6. Lời Kết
Qua quá trình tìm hiểu về quá trình đẳng tích, chúng ta đã có cái nhìn rõ ràng và sâu sắc hơn về cách thức các hệ thống khí hoạt động khi thể tích không thay đổi. Đồ thị đẳng tích, với đường thẳng thể hiện mối quan hệ giữa áp suất và nhiệt độ, là một minh chứng rõ ràng cho nguyên lý cơ bản trong nhiệt động lực học.
Hiểu biết về quá trình đẳng tích không chỉ có giá trị trong lý thuyết mà còn mang lại nhiều ứng dụng thực tiễn trong công nghiệp và khoa học. Từ việc dự đoán hành vi của khí trong các hệ thống nén khí cho đến việc áp dụng định luật Sác-lơ để giải quyết các vấn đề liên quan đến nhiệt độ và áp suất, kiến thức này thực sự rất quan trọng đối với các kỹ sư và nhà khoa học.
Bên cạnh đó, khi so sánh quá trình đẳng tích với quá trình đẳng nhiệt, chúng ta nhận ra rằng mặc dù cả hai đều là các biến đổi trạng thái của khí lý tưởng, nhưng mỗi quá trình lại có những đặc điểm riêng biệt cần được nắm vững để ứng dụng một cách hiệu quả trong thực tế.
Cuối cùng, việc hiểu rõ và áp dụng thành công các kiến thức về quá trình đẳng tích sẽ giúp chúng ta không chỉ nắm vững lý thuyết nhiệt động lực học mà còn có thể đối mặt với những thách thức trong nghiên cứu và phát triển công nghệ hiện đại. Hy vọng rằng qua bài viết này, các bạn đã có được những kiến thức bổ ích và sẵn sàng áp dụng chúng vào những bài tập, thí nghiệm hay các ứng dụng thực tế.