Đường Đẳng Tích: Khám Phá Chi Tiết và Ứng Dụng Thực Tiễn

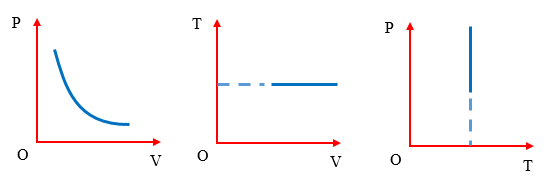
Đường đẳng tích là một khái niệm trong nhiệt động lực học, biểu diễn mối quan hệ giữa áp suất và nhiệt độ của một chất khí trong điều kiện thể tích không thay đổi. Trên hệ tọa độ (p, T), đường đẳng tích là một đường thẳng đi qua gốc tọa độ, cho thấy mối quan hệ tuyến tính giữa áp suất và nhiệt độ.

Trong quá trình đẳng tích, định luật Sác-lơ được áp dụng, phát biểu rằng áp suất của một lượng khí nhất định tỉ lệ thuận với nhiệt độ tuyệt đối khi thể tích không đổi. Công thức của định luật Sác-lơ được thể hiện như sau:

$$

P
T

=
hằng số

Cụ thể, khi áp dụng định luật này vào các quá trình thực tiễn, ta có thể sử dụng biểu thức:

$$


P
1


T
1


=


P
2


T
2

Ứng Dụng Của Đường Đẳng Tích

• Ứng dụng trong các bài toán vật lý như tính toán áp suất và nhiệt độ trong các hệ thống kín.
• Giúp hiểu rõ hành vi của chất khí khi bị thay đổi nhiệt độ mà thể tích được giữ cố định.
• Ứng dụng trong nghiên cứu và sản xuất, đặc biệt trong lĩnh vực công nghiệp.

Trong quá trình đẳng tích, định luật Sác-lơ được áp dụng, phát biểu rằng áp suất của một lượng khí nhất định tỉ lệ thuận với nhiệt độ tuyệt đối khi thể tích không đổi. Công thức của định luật Sác-lơ được thể hiện như sau:

$$

P
T

=
hằng số

Cụ thể, khi áp dụng định luật này vào các quá trình thực tiễn, ta có thể sử dụng biểu thức:

$$


P
1


T
1


=


P
2


T
2

Ứng Dụng Của Đường Đẳng Tích

• Ứng dụng trong các bài toán vật lý như tính toán áp suất và nhiệt độ trong các hệ thống kín.
• Giúp hiểu rõ hành vi của chất khí khi bị thay đổi nhiệt độ mà thể tích được giữ cố định.
• Ứng dụng trong nghiên cứu và sản xuất, đặc biệt trong lĩnh vực công nghiệp.

Đường đẳng tích là một khái niệm cơ bản trong nhiệt động lực học, mô tả mối quan hệ giữa áp suất và nhiệt độ của một lượng khí cố định khi thể tích không đổi. Đây là một phần quan trọng trong việc hiểu về các quá trình nhiệt động lực học và được ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý và công nghiệp.

Trong hệ tọa độ \(p\)-\(T\) (áp suất-nhiệt độ), đường đẳng tích được biểu diễn bằng một đường thẳng, thường bắt đầu từ gốc tọa độ khi áp suất bằng không và nhiệt độ tuyệt đối là zero. Đường này cho thấy rằng khi nhiệt độ tăng, áp suất của khí cũng tăng theo, miễn là thể tích được giữ cố định.

Khái niệm này không chỉ giúp lý giải các hiện tượng tự nhiên mà còn là cơ sở cho nhiều ứng dụng thực tiễn, từ thiết kế động cơ nhiệt đến việc nghiên cứu các quy luật khí lý tưởng. Bài viết sẽ đi sâu vào chi tiết của đường đẳng tích, giúp bạn có cái nhìn rõ nét và đầy đủ về khái niệm này.

Định luật Sác-lơ là một trong những định luật cơ bản của nhiệt động lực học, phát biểu rằng trong một quá trình đẳng tích (thể tích không đổi), áp suất của một lượng khí lý tưởng tỉ lệ thuận với nhiệt độ tuyệt đối của nó. Định luật này được biểu diễn bằng công thức:

\[ \frac{P}{T} = hằng số \]

Trong đó:

• \(P\) là áp suất của khí.
• \(T\) là nhiệt độ tuyệt đối của khí (đơn vị Kelvin).

Điều này có nghĩa là nếu nhiệt độ của khí tăng, áp suất cũng sẽ tăng tương ứng nếu thể tích không đổi. Định luật Sác-lơ giúp chúng ta hiểu rõ hơn về mối quan hệ giữa nhiệt độ và áp suất trong các quá trình đẳng tích và đóng vai trò quan trọng trong việc thiết kế các thiết bị và hệ thống liên quan đến khí nén.

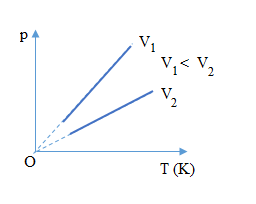
Để minh họa rõ ràng hơn, chúng ta có thể sử dụng đồ thị áp suất-nhiệt độ, trong đó đường đẳng tích là một đường thẳng dốc lên, cho thấy sự tỉ lệ thuận giữa áp suất và nhiệt độ trong một thể tích không đổi. Bài viết tiếp theo sẽ đi sâu vào việc áp dụng định luật này trong các tình huống thực tế và các ví dụ cụ thể.

Đường đẳng tích là một đường thẳng trên biểu đồ biểu diễn mối quan hệ giữa áp suất và nhiệt độ trong một quá trình đẳng tích, tức là thể tích của khí không thay đổi. Đặc điểm chính của đường đẳng tích là:

• Mối quan hệ tỉ lệ thuận: Áp suất của khí tỉ lệ thuận với nhiệt độ tuyệt đối khi thể tích được giữ cố định.
• Độ dốc của đường đẳng tích: Độ dốc của đường này phụ thuộc vào thể tích của hệ thống. Thể tích càng lớn, độ dốc của đường càng nhỏ.
• Điểm gốc của đường đẳng tích: Khi nhiệt độ tuyệt đối bằng không (0 K), áp suất của khí cũng bằng không, do đó đường đẳng tích đi qua gốc tọa độ.

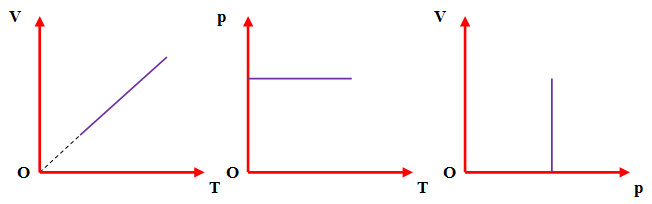
Biểu đồ đường đẳng tích thường được vẽ trong hệ tọa độ \((P, T)\), nơi:

• \(P\) là áp suất của khí (trục y).
• \(T\) là nhiệt độ tuyệt đối của khí (trục x).

Trên biểu đồ này, các đường đẳng tích là những đường thẳng dốc lên, cho thấy khi nhiệt độ tăng thì áp suất cũng tăng, miễn là thể tích không đổi.

Đường đẳng tích cung cấp cái nhìn trực quan về sự thay đổi áp suất của khí với nhiệt độ trong các điều kiện cố định, giúp dễ dàng hiểu và dự đoán hành vi của khí trong các hệ thống kín.

Để hiểu rõ hơn về đường đẳng tích, việc tiến hành các thí nghiệm thực tế là rất quan trọng. Dưới đây là một số thí nghiệm minh họa tiêu biểu:

• Thí nghiệm 1: Khí lý tưởng trong xilanh kín

  Chuẩn bị một xilanh kín có chứa khí lý tưởng, gắn nhiệt kế và áp kế để đo nhiệt độ và áp suất. Bắt đầu bằng cách gia nhiệt cho khí trong xilanh và quan sát sự thay đổi của áp suất khi nhiệt độ tăng. Trong thí nghiệm này, thể tích của khí được giữ cố định, do đó, theo định luật Sác-lơ, áp suất sẽ tăng tuyến tính với nhiệt độ.

• Thí nghiệm 2: Sự nở ra của khí trong một bóng cao su

  Đặt một quả bóng cao su chứa một lượng khí cố định vào nước nóng. Khi nước nóng làm tăng nhiệt độ của khí bên trong bóng, thể tích bóng bị giữ nguyên, nhưng áp suất bên trong tăng lên đáng kể, làm cho bóng căng phồng hơn. Đây là minh họa trực quan của đường đẳng tích trong thực tế.

• Thí nghiệm 3: Mô phỏng đường đẳng tích bằng phần mềm

  Sử dụng phần mềm mô phỏng nhiệt động lực học để quan sát sự thay đổi của áp suất khí theo nhiệt độ trong quá trình đẳng tích. Các phần mềm này cho phép hiển thị trực quan các biểu đồ \(P\)-\(T\), giúp người dùng dễ dàng hiểu rõ mối quan hệ giữa các đại lượng này trong quá trình đẳng tích.

Những thí nghiệm trên không chỉ minh họa lý thuyết về đường đẳng tích mà còn giúp chúng ta hiểu rõ hơn về ứng dụng của nó trong các tình huống thực tế.

Đường đẳng tích có nhiều ứng dụng quan trọng trong các lĩnh vực công nghiệp và đời sống hàng ngày. Việc hiểu rõ về mối quan hệ giữa áp suất và nhiệt độ trong điều kiện thể tích không đổi giúp chúng ta ứng dụng vào nhiều bài toán thực tế, từ sản xuất công nghiệp đến giải thích các hiện tượng tự nhiên.

1. Ứng dụng trong công nghiệp

Trong ngành công nghiệp, nguyên lý của quá trình đẳng tích được sử dụng để kiểm soát các hệ thống chịu áp suất, như nồi hơi, bình chứa khí và lốp xe. Đặc biệt, khi cần kiểm tra độ bền của các vật liệu chịu áp suất ở nhiệt độ cao, người ta thường sử dụng nguyên lý đẳng tích để tính toán và dự đoán sự thay đổi áp suất bên trong thiết bị.

• Nồi hơi: Trong quá trình đun nóng nước để tạo hơi, nếu thể tích không thay đổi, áp suất sẽ tăng lên tương ứng với nhiệt độ. Đây là nguyên lý được áp dụng để thiết kế van an toàn cho nồi hơi.
• Lốp xe: Áp suất bên trong lốp xe ô tô cũng tăng khi nhiệt độ tăng do ma sát trong quá trình di chuyển, nếu thể tích không thay đổi. Hiểu biết về đường đẳng tích giúp các kỹ sư thiết kế lốp xe an toàn hơn.

2. Ví dụ thực tiễn: Hiện tượng phồng bóng bàn trong nước nóng

Một ví dụ điển hình cho thấy sự ảnh hưởng của đường đẳng tích là hiện tượng một quả bóng bàn bị biến dạng khi được nhúng vào nước nóng. Khi quả bóng bị phồng do nhiệt độ tăng lên, áp suất bên trong bóng cũng tăng lên, làm quả bóng trở về hình dạng ban đầu. Đây là một minh chứng cho việc nhiệt độ tăng trong khi thể tích của quả bóng vẫn giữ nguyên, dẫn đến sự tăng áp suất bên trong theo định luật Sác-lơ.

3. Ảnh hưởng của đường đẳng tích đến đời sống hàng ngày

Trong đời sống hàng ngày, hiện tượng đẳng tích cũng xuất hiện khi chúng ta sử dụng các thiết bị như nồi áp suất, bình thủy tinh chứa chất lỏng, hoặc thậm chí khi làm nóng lốp xe đạp dưới ánh nắng mặt trời. Những hiểu biết về quá trình này giúp chúng ta sử dụng các thiết bị một cách an toàn và hiệu quả hơn, tránh các tai nạn không mong muốn do áp suất tăng đột ngột.

• Nồi áp suất: Khi đun nóng thức ăn trong nồi áp suất, áp suất tăng cao do thể tích cố định, giúp nấu chín thực phẩm nhanh chóng.
• Bình thủy tinh: Khi đun nóng nước trong bình thủy tinh bịt kín, nếu áp suất vượt quá sức chịu đựng của bình, có thể gây nổ.

Quá trình đẳng tích và đường đẳng tích đóng vai trò quan trọng trong việc hiểu biết và áp dụng các nguyên lý nhiệt động lực học. Đây không chỉ là nền tảng của nhiều hiện tượng vật lý mà còn có những ứng dụng thực tiễn quan trọng trong đời sống và công nghiệp.

Qua các nội dung đã trình bày, chúng ta có thể rút ra những điểm chính sau:

1. Khái niệm cơ bản: Đường đẳng tích biểu thị sự thay đổi áp suất theo nhiệt độ khi thể tích không đổi. Đây là một dạng quan trọng của quá trình biến đổi trạng thái trong chất khí.
2. Định luật Sác-lơ: Định luật này cho thấy sự phụ thuộc tuyến tính giữa áp suất và nhiệt độ của một lượng khí cố định trong điều kiện thể tích không đổi, là cơ sở lý thuyết cho nhiều ứng dụng thực tiễn.
3. Ứng dụng trong thực tế: Đường đẳng tích không chỉ được sử dụng trong các thí nghiệm vật lý, mà còn được ứng dụng trong các lĩnh vực như công nghiệp chế biến, công nghệ sản xuất, và các ngành khoa học nghiên cứu về nhiệt độ và áp suất.

Hiểu biết sâu sắc về đường đẳng tích giúp chúng ta nắm vững hơn các quy luật vật lý cơ bản và có thể áp dụng chúng vào nhiều lĩnh vực khác nhau. Điều này không chỉ góp phần vào việc phát triển khoa học kỹ thuật mà còn nâng cao chất lượng cuộc sống thông qua việc tối ưu hóa các quá trình nhiệt động lực học.

Đề xuất: Để tiếp tục phát triển và mở rộng kiến thức về nhiệt động lực học, cần có thêm các nghiên cứu chuyên sâu về sự tương tác giữa các biến số khác nhau trong quá trình đẳng tích, cũng như tìm kiếm các ứng dụng mới trong công nghệ và công nghiệp.