Chủ đề phương trình đẳng tích: Phương trình đẳng tích là một khái niệm quan trọng trong nhiệt động lực học, giúp hiểu rõ mối quan hệ giữa áp suất và nhiệt độ khi thể tích không thay đổi. Bài viết này sẽ cung cấp tất cả những thông tin chi tiết về định luật Sác-lơ, công thức toán học, và những ứng dụng thực tiễn của phương trình đẳng tích trong đời sống và công nghiệp.
Mục lục
Phương Trình Đẳng Tích: Khái Niệm và Ứng Dụng
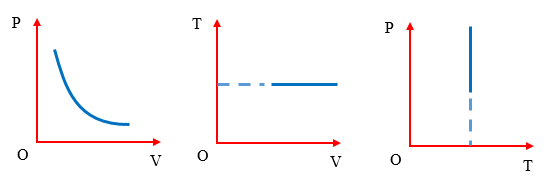
Phương trình đẳng tích là một khái niệm quan trọng trong lĩnh vực vật lý, đặc biệt là trong nghiên cứu các quá trình nhiệt động lực học của chất khí. Đây là phương trình mô tả mối quan hệ giữa áp suất và nhiệt độ của một lượng khí khi thể tích của nó được giữ cố định.
Định Luật Sác-lơ
Phương trình đẳng tích dựa trên định luật Sác-lơ, phát biểu rằng trong một quá trình đẳng tích, áp suất của một lượng khí nhất định tỉ lệ thuận với nhiệt độ tuyệt đối của nó. Điều này có nghĩa là khi nhiệt độ tăng, áp suất cũng tăng theo, với điều kiện thể tích không thay đổi.
Công Thức Của Phương Trình Đẳng Tích
Phương trình toán học biểu diễn mối quan hệ này được viết như sau:
\[
\frac{P_1}{T_1} = \frac{P_2}{T_2}
\]
Trong đó:
- \(P_1\) và \(T_1\) là áp suất và nhiệt độ tuyệt đối ở trạng thái ban đầu.
- \(P_2\) và \(T_2\) là áp suất và nhiệt độ tuyệt đối ở trạng thái sau.
Ứng Dụng Thực Tiễn
Phương trình đẳng tích không chỉ là một lý thuyết quan trọng trong giáo dục mà còn có nhiều ứng dụng thực tiễn. Nó giúp chúng ta hiểu rõ hơn về hành vi của các chất khí trong các điều kiện cụ thể, từ đó ứng dụng vào các bài toán nghiên cứu khoa học và các ngành công nghiệp như kỹ thuật cơ khí, nhiệt động lực học.
Ví Dụ Minh Họa
Một ví dụ điển hình của quá trình đẳng tích là khi khí trong một ống tiêm có pittong cố định được đun nóng. Trong trường hợp này, thể tích khí không thay đổi, nhưng áp suất tăng lên khi nhiệt độ tăng.
Bài Tập Ứng Dụng
Dưới đây là một số bài tập về quá trình đẳng tích để áp dụng kiến thức:
- Viết phương trình liên hệ giữa áp suất và nhiệt độ trong quá trình đẳng tích của một lượng khí nhất định.
- Phát biểu và giải thích định luật Sác-lơ.
- Tìm một ví dụ thực tế khác về quá trình đẳng tích và giải thích chi tiết.
Những kiến thức về phương trình đẳng tích không chỉ là nền tảng trong giáo dục mà còn mở ra nhiều hướng nghiên cứu và phát triển trong các ngành công nghiệp hiện đại.
.png)
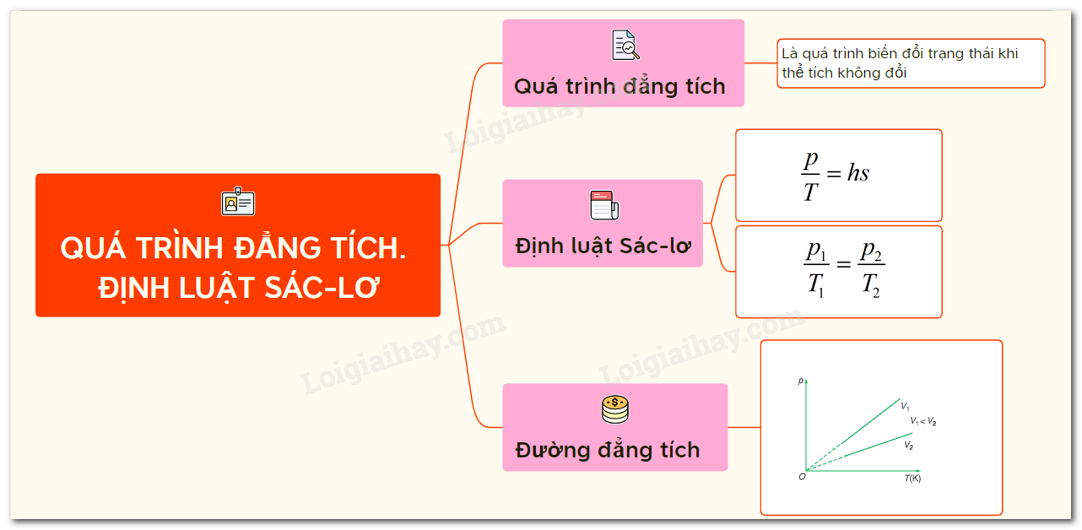
1. Giới Thiệu Chung Về Phương Trình Đẳng Tích
Phương trình đẳng tích là một khái niệm quan trọng trong lĩnh vực nhiệt động lực học, mô tả mối quan hệ giữa áp suất và nhiệt độ của một lượng khí nhất định khi thể tích được giữ cố định. Đây là một trong những quá trình cơ bản của chất khí lý tưởng, đóng vai trò nền tảng trong việc hiểu các hiện tượng liên quan đến chất khí.
Phương trình đẳng tích dựa trên định luật Sác-lơ, phát biểu rằng áp suất của một lượng khí lý tưởng tỉ lệ thuận với nhiệt độ tuyệt đối của nó, với điều kiện thể tích không thay đổi. Định luật này có thể được biểu diễn dưới dạng toán học như sau:
\[
\frac{P_1}{T_1} = \frac{P_2}{T_2}
\]
Trong phương trình này:
- \(P_1\) và \(T_1\) là áp suất và nhiệt độ ở trạng thái ban đầu.
- \(P_2\) và \(T_2\) là áp suất và nhiệt độ ở trạng thái sau.
Phương trình này cho thấy khi nhiệt độ của khí tăng lên, áp suất cũng tăng theo, miễn là thể tích không thay đổi. Điều này giải thích tại sao khi đun nóng một lượng khí trong một bình kín, áp suất bên trong bình sẽ tăng lên.
Phương trình đẳng tích không chỉ là một công cụ quan trọng trong nghiên cứu khoa học mà còn có nhiều ứng dụng thực tiễn trong các ngành công nghiệp như kỹ thuật cơ khí, hóa học, và các lĩnh vực liên quan đến việc quản lý chất khí.
2. Định Luật Sác-lơ và Phương Trình Đẳng Tích
Định luật Sác-lơ, được đặt tên theo nhà vật lý người Pháp Jacques Charles, là một trong những định luật cơ bản của nhiệt động lực học. Định luật này mô tả mối quan hệ giữa nhiệt độ và thể tích của một lượng khí lý tưởng, với điều kiện áp suất được giữ không đổi. Tuy nhiên, khi áp dụng vào quá trình đẳng tích, định luật này cho thấy sự thay đổi của áp suất khi nhiệt độ thay đổi, trong khi thể tích giữ nguyên.
Theo định luật Sác-lơ, khi thể tích của một khí lý tưởng được giữ cố định, áp suất của khí tỉ lệ thuận với nhiệt độ tuyệt đối. Điều này có thể được biểu diễn bằng phương trình sau:
\[
\frac{P_1}{T_1} = \frac{P_2}{T_2}
\]
Trong đó:
- \(P_1\) là áp suất ban đầu của khí.
- \(T_1\) là nhiệt độ ban đầu của khí, tính bằng Kelvin.
- \(P_2\) là áp suất sau khi nhiệt độ thay đổi.
- \(T_2\) là nhiệt độ mới của khí, tính bằng Kelvin.
Định luật này cho phép chúng ta hiểu rõ hơn về cách áp suất của một khí lý tưởng thay đổi khi nhiệt độ thay đổi trong điều kiện thể tích không đổi. Khi nhiệt độ tăng, các phân tử khí chuyển động nhanh hơn, dẫn đến việc va chạm mạnh hơn vào thành bình chứa, từ đó làm tăng áp suất.
Phương trình đẳng tích và định luật Sác-lơ không chỉ là những kiến thức lý thuyết quan trọng mà còn có ứng dụng thực tế rộng rãi trong các ngành công nghiệp, như sản xuất động cơ và thiết bị nhiệt, nơi mà việc kiểm soát áp suất và nhiệt độ là cực kỳ quan trọng.

3. Ứng Dụng Thực Tiễn Của Phương Trình Đẳng Tích
Phương trình đẳng tích có nhiều ứng dụng thực tiễn trong các lĩnh vực khoa học và công nghiệp, đặc biệt là trong việc hiểu và điều chỉnh các quá trình nhiệt động lực học. Dưới đây là một số ứng dụng tiêu biểu:
- Thiết kế và vận hành động cơ nhiệt: Trong các động cơ đốt trong, phương trình đẳng tích giúp các kỹ sư hiểu rõ mối quan hệ giữa nhiệt độ và áp suất khi thể tích không đổi, từ đó tối ưu hóa hiệu suất động cơ.
- Hệ thống làm lạnh và điều hòa không khí: Phương trình đẳng tích được áp dụng trong việc tính toán và kiểm soát áp suất của chất làm lạnh khi nhiệt độ thay đổi trong các hệ thống này, đảm bảo hiệu suất và an toàn.
- Các quá trình hóa học trong công nghiệp: Trong các phản ứng hóa học diễn ra trong các bình kín, việc hiểu rõ sự biến đổi áp suất theo nhiệt độ giúp tối ưu hóa quá trình phản ứng, từ đó tăng hiệu suất và giảm chi phí sản xuất.
- Nghiên cứu và phát triển vật liệu: Phương trình đẳng tích được sử dụng trong việc nghiên cứu tính chất nhiệt động lực học của các vật liệu mới, đặc biệt là các vật liệu chịu nhiệt, giúp phát triển các sản phẩm có khả năng chịu nhiệt cao và bền bỉ.
Nhìn chung, phương trình đẳng tích không chỉ là một công cụ quan trọng trong lý thuyết mà còn là nền tảng cho nhiều ứng dụng thực tiễn, đóng góp vào sự phát triển của nhiều ngành công nghiệp hiện đại.
4. Ví Dụ Minh Họa Về Phương Trình Đẳng Tích
Để hiểu rõ hơn về phương trình đẳng tích, chúng ta sẽ xem xét một ví dụ minh họa dưới đây. Ví dụ này sẽ giúp bạn nắm bắt cách áp dụng phương trình trong thực tế.
Ví dụ: Giả sử chúng ta có một bình chứa khí lý tưởng với thể tích không đổi là \(V = 10 \, \text{lít}\). Khí trong bình có áp suất ban đầu là \(P_1 = 2 \, \text{atm}\) và nhiệt độ ban đầu là \(T_1 = 300 \, \text{K}\). Bây giờ, chúng ta tăng nhiệt độ của khí lên \(T_2 = 450 \, \text{K}\). Hỏi áp suất mới \(P_2\) trong bình là bao nhiêu?
Áp dụng phương trình đẳng tích:
Thay các giá trị vào phương trình:
Giải phương trình để tìm \(P_2\):
Vậy áp suất mới \(P_2\) là \(3 \, \text{atm}\).
Qua ví dụ trên, chúng ta thấy rằng khi nhiệt độ của khí tăng trong điều kiện thể tích không đổi, áp suất của khí cũng tăng theo tỷ lệ thuận. Đây là một ứng dụng thực tế của phương trình đẳng tích trong việc dự đoán sự thay đổi áp suất khi nhiệt độ biến đổi trong các hệ kín.

5. Kết Luận
Phương trình đẳng tích không chỉ là một khái niệm cơ bản trong vật lý nhiệt động lực học, mà còn có nhiều ứng dụng thực tiễn trong các ngành công nghiệp và nghiên cứu khoa học. Nhờ vào khả năng dự đoán mối quan hệ giữa áp suất và nhiệt độ khi thể tích không đổi, phương trình này đã trở thành công cụ đắc lực trong việc thiết kế và vận hành các hệ thống liên quan đến chất khí.
Qua các nghiên cứu và thí nghiệm, chúng ta đã thấy rõ rằng đường đẳng tích, được biểu diễn trên hệ tọa độ áp suất - nhiệt độ, là một công cụ mạnh mẽ để hiểu rõ hơn về hành vi của các chất khí. Đường đẳng tích không chỉ giúp chúng ta nắm bắt được mối quan hệ tuyến tính giữa áp suất và nhiệt độ, mà còn cung cấp cái nhìn sâu sắc về sự biến đổi trạng thái của chất khí dưới các điều kiện cụ thể.
Việc hiểu và ứng dụng phương trình đẳng tích không chỉ giới hạn trong lý thuyết mà còn mở rộng ra thực tế, từ việc phát triển các công nghệ mới trong công nghiệp, đến cải tiến các quá trình sản xuất và nghiên cứu khoa học. Tầm quan trọng của phương trình này càng được khẳng định khi nó đóng vai trò không thể thiếu trong việc nâng cao hiệu suất và độ an toàn của các hệ thống làm việc với khí, đặc biệt là trong các lĩnh vực yêu cầu sự kiểm soát chính xác của các thông số nhiệt động lực học.
Tóm lại, phương trình đẳng tích đã và đang tiếp tục chứng tỏ giá trị của mình trong nhiều lĩnh vực. Sự hiểu biết và ứng dụng thành thạo phương trình này sẽ không chỉ giúp các kỹ sư, nhà nghiên cứu đạt được những bước tiến lớn trong công việc của họ mà còn đóng góp vào sự phát triển chung của khoa học và công nghệ.