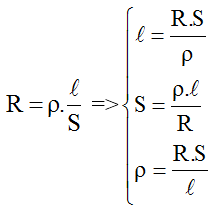Công Thức Tính Điện Trở Của 1 Dây Dẫn Là Gì? Khám Phá Chi Tiết Và Ứng Dụng Thực Tiễn

Điện trở của một dây dẫn là đại lượng đặc trưng cho khả năng cản trở dòng điện của dây dẫn đó. Điện trở này phụ thuộc vào nhiều yếu tố như chiều dài, tiết diện và điện trở suất của vật liệu làm dây dẫn. Dưới đây là các công thức và lý thuyết liên quan đến việc tính toán điện trở của dây dẫn.

1. Công Thức Tính Điện Trở

Điện trở của một dây dẫn được tính bằng công thức:

\[
R = \frac{\rho \cdot L}{S}
\]

• \(R\) : Điện trở của dây dẫn (\(\Omega\))
• \(\rho\) : Điện trở suất của vật liệu làm dây dẫn (\(\Omega \cdot m\))
• \(L\) : Chiều dài của dây dẫn (m)
• \(S\) : Tiết diện của dây dẫn (\(m^2\))

2. Ảnh Hưởng Của Các Yếu Tố Đến Điện Trở

Điện trở của dây dẫn tỷ lệ thuận với chiều dài \(L\) của dây và điện trở suất \(\rho\) của vật liệu. Đồng thời, điện trở tỷ lệ nghịch với tiết diện \(S\) của dây dẫn. Cụ thể:

• Khi chiều dài \(L\) tăng, điện trở \(R\) cũng tăng.
• Khi tiết diện \(S\) tăng, điện trở \(R\) giảm.
• Vật liệu có điện trở suất \(\rho\) càng lớn thì điện trở của dây dẫn càng cao.

3. Ví Dụ Minh Họa

Giả sử ta có một dây dẫn bằng đồng với các thông số sau:

• Chiều dài \(L = 100 m\)
• Tiết diện \(S = 1 mm^2 = 1 \times 10^{-6} m^2\)
• Điện trở suất của đồng \(\rho = 1.68 \times 10^{-8} \Omega \cdot m\)

Điện trở của dây dẫn này được tính như sau:

\[
R = \frac{1.68 \times 10^{-8} \times 100}{1 \times 10^{-6}} = 0.168 \, \Omega
\]

4. Ứng Dụng Thực Tiễn

Công thức tính điện trở của dây dẫn được ứng dụng rộng rãi trong thiết kế mạch điện, kiểm tra chất lượng dây dẫn, và tính toán sức chịu tải của dây dẫn trong các hệ thống điện. Điện trở là yếu tố quan trọng để đảm bảo an toàn và hiệu quả trong truyền tải điện năng.

• Thiết kế mạch điện: Giúp chọn lựa vật liệu và kích thước dây dẫn phù hợp.
• Kiểm tra chất lượng: Đo điện trở để kiểm tra độ tin cậy của dây dẫn.
• Tính toán sức chịu tải: Xác định giới hạn an toàn của dây dẫn.

5. Bài Tập Thực Hành

Để hiểu rõ hơn về công thức tính điện trở, bạn có thể thực hiện một số bài tập sau:

1. Tính điện trở của một dây dẫn bằng đồng dài 50m, có tiết diện 0.5mm².
2. Một dây dẫn nicrom dài 10m, tiết diện 0.2mm², có điện trở suất 1.10×10⁻⁶ Ω·m. Tính điện trở của dây dẫn này.

Hy vọng với các thông tin trên, bạn có thể hiểu rõ hơn về công thức tính điện trở của dây dẫn và áp dụng nó trong các tình huống thực tế.

Điện trở là đại lượng đặc trưng cho khả năng cản trở dòng điện của một vật liệu dẫn điện khi có dòng điện chạy qua. Khái niệm này được sử dụng rộng rãi trong các lĩnh vực kỹ thuật và vật lý, đặc biệt là trong thiết kế và phân tích mạch điện.

Điện trở của một dây dẫn phụ thuộc vào ba yếu tố chính:

• Điện trở suất (\(\rho\)): Đây là một hằng số vật lý đặc trưng cho mỗi loại vật liệu. Điện trở suất càng cao thì điện trở của vật liệu càng lớn.
• Chiều dài dây dẫn (\(L\)): Điện trở tỉ lệ thuận với chiều dài của dây dẫn. Dây dẫn càng dài, điện trở càng lớn.
• Tiết diện dây dẫn (\(S\)): Điện trở tỉ lệ nghịch với tiết diện của dây dẫn. Dây dẫn có tiết diện càng lớn thì điện trở càng nhỏ.

Điện trở của dây dẫn được tính bằng công thức:

\[
R = \frac{\rho \cdot L}{S}
\]

Trong đó:

• \(R\) là điện trở của dây dẫn (\(\Omega\)).
• \(\rho\) là điện trở suất của vật liệu (\(\Omega \cdot m\)).
• \(L\) là chiều dài của dây dẫn (m).
• \(S\) là tiết diện của dây dẫn (\(m^2\)).

Như vậy, điện trở là một yếu tố quan trọng trong việc tính toán và thiết kế mạch điện, giúp xác định mức độ tiêu hao năng lượng và hiệu suất của hệ thống điện.

Công thức tính điện trở của một dây dẫn là một trong những công thức cơ bản và quan trọng trong lĩnh vực điện học. Công thức này giúp ta xác định mức độ cản trở của dây dẫn đối với dòng điện đi qua, dựa trên các yếu tố như chiều dài, tiết diện, và điện trở suất của vật liệu.

Điện trở \(R\) của một dây dẫn được tính bằng công thức:

\[
R = \frac{\rho \cdot L}{S}
\]

Trong đó:

• \(\rho\) là điện trở suất của vật liệu làm dây dẫn, đơn vị là \(\Omega \cdot m\). Điện trở suất biểu thị khả năng cản trở dòng điện của một vật liệu, và nó phụ thuộc vào tính chất của vật liệu đó. Ví dụ, đồng có điện trở suất thấp hơn so với sắt, do đó dây dẫn bằng đồng sẽ có điện trở thấp hơn dây dẫn cùng kích thước nhưng làm từ sắt.
• \(L\) là chiều dài của dây dẫn, đơn vị là mét (m). Chiều dài càng lớn thì điện trở càng cao, bởi vì dòng điện phải đi qua một quãng đường dài hơn, gặp nhiều vật cản hơn.
• \(S\) là tiết diện ngang của dây dẫn, đơn vị là mét vuông (\(m^2\)). Tiết diện càng lớn thì điện trở càng nhỏ, do dòng điện có nhiều "lối đi" hơn để đi qua dây dẫn.

Công thức trên cho thấy rằng điện trở của một dây dẫn tỉ lệ thuận với chiều dài của dây và điện trở suất của vật liệu, đồng thời tỉ lệ nghịch với tiết diện của dây. Do đó, để giảm điện trở, ta có thể chọn vật liệu có điện trở suất thấp hơn, tăng tiết diện hoặc giảm chiều dài của dây dẫn.

Ví dụ: Để tính điện trở của một dây dẫn đồng dài 100m, với tiết diện ngang là 1mm² (\(1 \times 10^{-6} m^2\)), và điện trở suất của đồng là \(\rho = 1.68 \times 10^{-8} \Omega \cdot m\), ta áp dụng công thức:

\[
R = \frac{1.68 \times 10^{-8} \times 100}{1 \times 10^{-6}} = 0.168 \, \Omega
\]

Điện trở của dây dẫn này là 0.168 \(\Omega\).

Như vậy, công thức tính điện trở là một công cụ mạnh mẽ để thiết kế và tối ưu hóa các hệ thống điện, giúp đảm bảo hiệu quả và an toàn trong quá trình truyền tải điện năng.

Công thức tính điện trở không chỉ là một lý thuyết cơ bản trong vật lý mà còn có rất nhiều ứng dụng thực tiễn trong đời sống và các ngành công nghiệp. Dưới đây là một số ứng dụng quan trọng của công thức này.

3.1. Thiết Kế Và Kiểm Tra Hệ Thống Điện

Trong thiết kế các hệ thống điện, việc tính toán điện trở của dây dẫn giúp đảm bảo rằng hệ thống hoạt động hiệu quả và an toàn. Điện trở càng thấp, tổn hao năng lượng càng ít, điều này rất quan trọng trong các hệ thống truyền tải điện năng lớn. Ngoài ra, kiểm tra điện trở của dây dẫn cũng giúp phát hiện sự cố như đứt gãy hoặc ăn mòn, từ đó ngăn ngừa nguy cơ chập cháy.

3.2. Ứng Dụng Trong Thiết Bị Điện Tử

Các thiết bị điện tử, như mạch tích hợp, vi mạch, và các cảm biến, đều yêu cầu thiết kế chính xác về điện trở để đảm bảo hoạt động ổn định. Ví dụ, điện trở trong các mạch điều khiển được tính toán kỹ lưỡng để điều chỉnh mức điện áp và dòng điện, đảm bảo hoạt động chính xác của thiết bị.

3.3. Tính Toán Tổn Hao Năng Lượng Trong Dây Dẫn

Trong các hệ thống điện, đặc biệt là truyền tải điện năng qua khoảng cách xa, tổn hao năng lượng do điện trở của dây dẫn là một yếu tố quan trọng cần tính toán. Công thức tính điện trở giúp kỹ sư dự đoán mức độ tổn hao này và tìm cách giảm thiểu nó, chẳng hạn bằng cách tăng tiết diện dây dẫn hoặc sử dụng vật liệu dẫn điện có điện trở suất thấp.

3.4. Đánh Giá Chất Lượng Vật Liệu

Điện trở suất là một trong những chỉ số quan trọng để đánh giá chất lượng của vật liệu dẫn điện. Thông qua việc đo lường và tính toán điện trở, các nhà khoa học và kỹ sư có thể xác định được đặc tính của vật liệu, từ đó lựa chọn vật liệu phù hợp cho từng ứng dụng cụ thể.

3.5. Ứng Dụng Trong Các Thiết Bị Gia Dụng

Các thiết bị gia dụng như máy nước nóng, bếp điện, và bàn ủi đều sử dụng dây dẫn có điện trở được thiết kế phù hợp để chuyển hóa năng lượng điện thành nhiệt năng. Việc tính toán chính xác điện trở giúp các thiết bị này hoạt động hiệu quả và an toàn, đảm bảo cung cấp nhiệt độ ổn định.

Như vậy, công thức tính điện trở không chỉ giúp hiểu rõ hơn về các nguyên lý điện học mà còn là công cụ quan trọng trong việc thiết kế, kiểm tra và tối ưu hóa các hệ thống và thiết bị điện trong thực tế.

Trong phần này, chúng ta sẽ tìm hiểu một số bài tập và ví dụ minh họa giúp bạn hiểu rõ hơn về công thức tính điện trở của một dây dẫn. Các bài tập sẽ giúp bạn áp dụng lý thuyết vào thực tế và kiểm tra khả năng hiểu biết của mình.

4.1. Bài Tập Tính Điện Trở Cơ Bản

Hãy giải bài tập sau để nắm vững cách tính điện trở của một dây dẫn trong các điều kiện cơ bản:

1. Cho một dây dẫn có chiều dài 10 m, tiết diện 2 mm² và điện trở suất của vật liệu là 1.7 × 10^-8 Ω·m. Tính điện trở của dây dẫn.

   Áp dụng công thức tính điện trở:

   \[ R = \rho \frac{L}{A} \]

   Trong đó:

   • \( \rho \) là điện trở suất của vật liệu (1.7 × 10^-8 Ω·m)
   • \( L \) là chiều dài dây dẫn (10 m)
   • \( A \) là tiết diện của dây dẫn (2 mm² = 2 × 10^-6 m²)

   Thay số vào công thức:

   \[ R = 1.7 \times 10^{-8} \frac{10}{2 \times 10^{-6}} = 0.085 \, \Omega \]

4.2. Bài Tập Tính Điện Trở Nâng Cao

Hãy thử sức với bài tập nâng cao sau để kiểm tra sự hiểu biết của bạn về điện trở trong các mạch phức tạp hơn:

1. Có một mạch điện gồm ba dây dẫn mắc nối tiếp với các điện trở suất khác nhau. Dây dẫn đầu tiên có chiều dài 5 m, tiết diện 1 mm² và điện trở suất 2 × 10^-8 Ω·m. Dây dẫn thứ hai có chiều dài 3 m, tiết diện 1.5 mm² và điện trở suất 3 × 10^-8 Ω·m. Dây dẫn thứ ba có chiều dài 4 m, tiết diện 2 mm² và điện trở suất 1.5 × 10^-8 Ω·m. Tính tổng điện trở của mạch.

   Đầu tiên, tính điện trở của từng dây dẫn bằng công thức:

   \[ R = \rho \frac{L}{A} \]

   Với các giá trị cụ thể:

   • Dây dẫn 1: \[ R_1 = 2 \times 10^{-8} \frac{5}{1 \times 10^{-6}} = 0.1 \, \Omega \]
   • Dây dẫn 2: \[ R_2 = 3 \times 10^{-8} \frac{3}{1.5 \times 10^{-6}} = 0.06 \, \Omega \]
   • Dây dẫn 3: \[ R_3 = 1.5 \times 10^{-8} \frac{4}{2 \times 10^{-6}} = 0.03 \, \Omega \]

   Tổng điện trở của mạch nối tiếp là tổng của các điện trở:

   \[ R_{tổng} = R_1 + R_2 + R_3 = 0.1 + 0.06 + 0.03 = 0.19 \, \Omega \]

4.3. Ví Dụ Thực Tế Về Ứng Dụng Công Thức Tính Điện Trở

Dưới đây là một ví dụ thực tế về ứng dụng công thức tính điện trở trong thiết kế mạch điện:

Giả sử bạn đang thiết kế một mạch điện cho một thiết bị điện tử. Bạn cần chọn điện trở phù hợp để điều chỉnh dòng điện qua một linh kiện nhất định. Bạn biết rằng linh kiện cần dòng điện không vượt quá 0.5 A và nguồn điện áp là 12 V. Bạn có thể tính giá trị điện trở cần thiết như sau:

Áp dụng định luật Ohm:

\[ R = \frac{V}{I} \]

Trong đó:

• \( V \) là điện áp (12 V)
• \( I \) là dòng điện (0.5 A)

Thay số vào công thức:

\[ R = \frac{12}{0.5} = 24 \, \Omega \]

Do đó, bạn cần một điện trở có giá trị 24 Ω để đảm bảo dòng điện không vượt quá 0.5 A.

Để giảm tổn thất năng lượng do điện trở trong các mạch điện, có thể áp dụng một số biện pháp kỹ thuật sau đây. Những biện pháp này giúp tăng hiệu suất hệ thống điện và tiết kiệm năng lượng hiệu quả.

5.1. Lựa Chọn Vật Liệu Dẫn Điện Tốt

Việc chọn vật liệu dẫn điện có điện trở suất thấp là một trong những phương pháp quan trọng để giảm tổn thất năng lượng. Các vật liệu như đồng và nhôm thường được sử dụng trong dây dẫn điện vì chúng có điện trở suất thấp, giúp giảm tổn thất năng lượng trong quá trình truyền tải.

• Đồng: Có điện trở suất khoảng 1.7 × 10^-8 Ω·m, rất tốt cho các ứng dụng yêu cầu dẫn điện hiệu quả.
• Nhôm: Có điện trở suất khoảng 2.8 × 10^-8 Ω·m, thường được sử dụng trong các ứng dụng truyền tải điện năng lớn.

5.2. Tăng Tiết Diện Dây Dẫn

Tăng tiết diện của dây dẫn là một biện pháp hiệu quả để giảm điện trở và do đó giảm tổn thất năng lượng. Khi tiết diện dây dẫn lớn hơn, điện trở của nó sẽ giảm theo công thức:

\[ R = \rho \frac{L}{A} \]

Trong đó:

• \( \rho \) là điện trở suất của vật liệu
• \( L \) là chiều dài dây dẫn
• \( A \) là tiết diện dây dẫn

Khi tăng \( A \), điện trở \( R \) giảm, từ đó tổn thất năng lượng giảm theo. Ví dụ, việc sử dụng cáp điện có tiết diện lớn hơn sẽ giúp giảm tổn thất năng lượng trong hệ thống truyền tải điện.

5.3. Sử Dụng Điện Áp Cao Trong Truyền Tải

Để giảm tổn thất năng lượng trong quá trình truyền tải điện, một phương pháp phổ biến là sử dụng điện áp cao. Khi truyền tải điện ở điện áp cao, dòng điện sẽ giảm, và do đó tổn thất năng lượng theo công thức:

\[ P_{\text{tổn thất}} = I^2 R \]

Trong đó:

• \( P_{\text{tổn thất}} \) là tổn thất năng lượng
• \( I \) là dòng điện
• \( R \) là điện trở của dây dẫn

Giảm dòng điện bằng cách tăng điện áp giúp giảm tổn thất năng lượng. Ví dụ, trong hệ thống truyền tải điện năng lớn, điện áp cao (như 110 kV hoặc 220 kV) thường được sử dụng để giảm tổn thất điện năng trong các dây dẫn dài.

Trong tài liệu này, chúng ta đã tìm hiểu về các khái niệm cơ bản và công thức tính điện trở của một dây dẫn. Dưới đây là những điểm chính và kết luận quan trọng từ nội dung đã được trình bày:

• Khái Niệm Điện Trở: Điện trở là đặc tính của một dây dẫn làm cản trở dòng điện, và nó phụ thuộc vào điện trở suất của vật liệu, chiều dài và tiết diện của dây dẫn.
• Công Thức Tính Điện Trở: Công thức tổng quát để tính điện trở là:

\[ R = \rho \frac{L}{A} \]

• Ứng Dụng Công Thức: Công thức này có thể được áp dụng để tính điện trở trong các mạch nối tiếp và song song, cũng như trong việc thiết kế mạch điện và kiểm tra chất lượng dây dẫn.
• Biện Pháp Giảm Tổn Thất Năng Lượng: Để giảm tổn thất năng lượng do điện trở, có thể áp dụng các biện pháp như lựa chọn vật liệu dẫn điện tốt, tăng tiết diện dây dẫn, và sử dụng điện áp cao trong truyền tải.

Việc hiểu và áp dụng chính xác công thức tính điện trở không chỉ giúp chúng ta trong việc thiết kế và tối ưu hóa các mạch điện mà còn trong việc cải thiện hiệu suất và tiết kiệm năng lượng trong các hệ thống điện. Hy vọng rằng tài liệu này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn có thêm kiến thức về điện trở của dây dẫn.