Chủ đề công thức tính điện trở suất lớp 11: Công thức tính điện trở suất lớp 11 là một trong những kiến thức vật lý quan trọng và cơ bản. Bài viết này sẽ giúp bạn hiểu rõ hơn về công thức, các yếu tố ảnh hưởng, và cách áp dụng vào thực tế. Đừng bỏ lỡ cơ hội nắm vững kiến thức này để tự tin trong học tập và ứng dụng trong đời sống!
Mục lục
Công Thức Tính Điện Trở Suất Lớp 11
Điện trở suất là một đại lượng vật lý quan trọng trong lĩnh vực điện học. Nó biểu thị khả năng của một chất dẫn điện trong việc cản trở dòng điện. Điện trở suất thường được ký hiệu bằng chữ cái Hy Lạp \( \rho \) (rho) và có đơn vị đo là Ohm-mét (Ω⋅m).
1. Công Thức Tính Điện Trở Suất
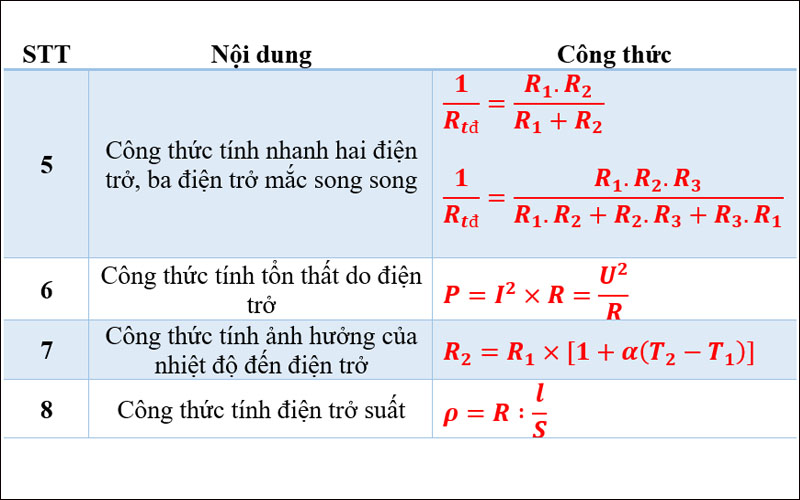
Công thức chung để tính điện trở suất là:
\[
\rho = \frac{R \cdot A}{l}
\]
Trong đó:
- \( \rho \) là điện trở suất (đơn vị: Ω⋅m).
- \( R \) là điện trở của đoạn dây dẫn (đơn vị: Ω).
- \( A \) là diện tích mặt cắt ngang của dây dẫn (đơn vị: m²).
- \( l \) là chiều dài của đoạn dây dẫn (đơn vị: m).
2. Ứng Dụng Công Thức
Công thức này được sử dụng để tính điện trở suất của một chất khi biết các thông số về điện trở, diện tích mặt cắt và chiều dài của vật liệu đó. Đây là công thức cơ bản và rất quan trọng trong việc phân tích và thiết kế các mạch điện, cũng như trong ngành công nghiệp điện tử.
3. Điện Trở Suất Của Một Số Kim Loại Thông Dụng
| Kim loại | Điện trở suất \( \rho \) (Ω⋅m) |
|---|---|
| Bạc | 1,6 x 10-8 |
| Đồng | 1,7 x 10-8 |
| Nhôm | 2,8 x 10-8 |
| Vonfram | 5,5 x 10-8 |
| Sắt | 12,0 x 10-8 |
4. Sự Phụ Thuộc Của Điện Trở Suất Theo Nhiệt Độ
Điện trở suất của các chất dẫn điện thường tăng khi nhiệt độ tăng. Công thức mô tả sự phụ thuộc này là:
\[
\rho = \rho_0 \cdot [1 + \alpha \cdot (t - t_0)]
\]
Trong đó:
- \( \rho \) là điện trở suất tại nhiệt độ \( t \).
- \( \rho_0 \) là điện trở suất tại nhiệt độ ban đầu \( t_0 \).
- \( \alpha \) là hệ số nhiệt điện trở (đơn vị: K-1).
- \( t \) và \( t_0 \) là nhiệt độ lúc sau và lúc đầu (đơn vị: °C hoặc K).
5. Kết Luận
Hiểu rõ công thức tính điện trở suất và cách áp dụng nó là rất quan trọng trong việc giải quyết các bài toán về điện, đặc biệt trong lĩnh vực điện tử và kỹ thuật điện. Điện trở suất không chỉ giúp xác định khả năng dẫn điện của vật liệu mà còn là yếu tố chính ảnh hưởng đến thiết kế và hiệu suất của các thiết bị điện.
.png)
Mục Lục Tổng Hợp
-
1. Khái Niệm Và Định Nghĩa Về Điện Trở Suất
1.1. Điện Trở Suất Là Gì?
1.2. Đơn Vị Đo Lường Và Ký Hiệu Của Điện Trở Suất
-
2. Công Thức Tính Điện Trở Suất Lớp 11
2.1. Công Thức Cơ Bản
2.2. Ví Dụ Minh Họa Công Thức Tính Điện Trở Suất
2.3. Các Yếu Tố Ảnh Hưởng Đến Điện Trở Suất
-
3. Bảng Điện Trở Suất Của Một Số Vật Liệu Thường Gặp
3.1. Điện Trở Suất Của Các Kim Loại Phổ Biến
3.2. Điện Trở Suất Của Một Số Vật Liệu Phi Kim
-
4. Ứng Dụng Của Điện Trở Suất Trong Thực Tế
4.1. Ứng Dụng Trong Ngành Kỹ Thuật Điện
4.2. Ứng Dụng Trong Các Bài Toán Vật Lý Lớp 11
-
5. Sự Phụ Thuộc Của Điện Trở Suất Theo Nhiệt Độ
5.1. Mối Quan Hệ Giữa Nhiệt Độ Và Điện Trở Suất
5.2. Công Thức Tính Điện Trở Suất Khi Nhiệt Độ Thay Đổi
-
6. Bài Tập Về Điện Trở Suất
6.1. Bài Tập Tính Toán Cơ Bản
6.2. Bài Tập Ứng Dụng Thực Tế
1. Khái Niệm Điện Trở Suất
Điện trở suất là một đại lượng vật lý đặc trưng cho khả năng cản trở dòng điện của một vật liệu. Điện trở suất thường được ký hiệu bằng chữ cái Hy Lạp \( \rho \) (rho) và có đơn vị là Ohm-mét (Ω⋅m). Về cơ bản, điện trở suất cho biết mức độ dễ dàng hay khó khăn của các hạt điện tích khi di chuyển qua một vật liệu dẫn điện.
Cụ thể, điện trở suất của một vật liệu càng lớn thì khả năng dẫn điện của vật liệu đó càng kém và ngược lại. Điện trở suất phụ thuộc vào bản chất của vật liệu và thường biến đổi theo nhiệt độ, áp suất và các yếu tố ngoại vi khác.
- Đơn Vị Của Điện Trở Suất: Đơn vị của điện trở suất trong hệ SI là Ohm-mét (Ω⋅m).
- Ký Hiệu: Điện trở suất được ký hiệu bằng \( \rho \).
Điện trở suất là một khái niệm quan trọng trong vật lý và kỹ thuật điện, giúp xác định mức độ hiệu quả của vật liệu khi được sử dụng làm dây dẫn trong các mạch điện. Việc hiểu rõ khái niệm và công thức tính điện trở suất là nền tảng để giải quyết các bài toán liên quan đến điện trong chương trình Vật lý lớp 11.

2. Công Thức Tính Điện Trở Suất
Điện trở suất của một vật liệu được xác định thông qua công thức cơ bản dưới đây, dựa trên điện trở của một đoạn dây dẫn có chiều dài và tiết diện xác định:
\[
\rho = \frac{R \cdot A}{l}
\]
Trong đó:
- \( \rho \): Điện trở suất của vật liệu (đơn vị: Ω⋅m).
- \( R \): Điện trở của đoạn dây dẫn (đơn vị: Ω).
- \( A \): Diện tích mặt cắt ngang của dây dẫn (đơn vị: m²).
- \( l \): Chiều dài của đoạn dây dẫn (đơn vị: m).
Điện trở suất \( \rho \) là một đại lượng đặc trưng cho khả năng cản trở dòng điện của một vật liệu cụ thể. Trong công thức trên:
Điện trở \( R \): Điện trở của một vật liệu dẫn điện phụ thuộc vào vật liệu đó có tính dẫn điện tốt hay không. Một vật liệu có điện trở thấp thường có khả năng dẫn điện tốt hơn.
Diện tích mặt cắt ngang \( A \): Diện tích của mặt cắt ngang càng lớn thì dòng điện đi qua vật liệu càng dễ dàng, làm giảm điện trở.
Chiều dài \( l \): Chiều dài của dây dẫn càng dài, điện trở càng tăng vì các electron phải di chuyển qua một đoạn đường dài hơn.
Như vậy, để tính toán điện trở suất của một vật liệu, chúng ta cần biết được giá trị của điện trở, diện tích mặt cắt ngang và chiều dài của vật liệu đó. Hiểu rõ công thức này giúp ta ứng dụng hiệu quả trong các bài toán vật lý liên quan đến điện và trong thiết kế các mạch điện trong thực tế.
3. Bảng Điện Trở Suất Của Một Số Vật Liệu
Dưới đây là bảng điện trở suất của một số vật liệu thường gặp trong các bài toán vật lý và ứng dụng kỹ thuật. Bảng này giúp bạn có cái nhìn tổng quan về khả năng dẫn điện của các vật liệu khác nhau:
| Vật Liệu | Điện Trở Suất \(\rho\) (Ω⋅m) |
|---|---|
| Đồng (Cu) | \(1.68 \times 10^{-8}\) |
| Nhôm (Al) | \(2.82 \times 10^{-8}\) |
| Vàng (Au) | \(2.44 \times 10^{-8}\) |
| Sắt (Fe) | \(9.71 \times 10^{-8}\) |
| Bạc (Ag) | \(1.59 \times 10^{-8}\) |
| Thủy ngân (Hg) | \(9.8 \times 10^{-7}\) |
| Nhựa (Plastic) | \(10^{10} - 10^{15}\) |
| Thủy tinh (Glass) | \(10^{10} - 10^{14}\) |
Như bảng trên cho thấy, kim loại như đồng, nhôm, và bạc có điện trở suất rất thấp, cho thấy chúng có khả năng dẫn điện tốt. Ngược lại, các vật liệu như nhựa và thủy tinh có điện trở suất rất cao, làm cho chúng trở thành những chất cách điện tốt.
Bảng điện trở suất này không chỉ có ý nghĩa trong việc giải các bài toán vật lý mà còn được ứng dụng rộng rãi trong ngành kỹ thuật điện và các ngành công nghiệp khác, giúp lựa chọn vật liệu phù hợp cho các thiết bị và mạch điện.

4. Ứng Dụng Của Công Thức Điện Trở Suất
Công thức điện trở suất không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống và kỹ thuật. Dưới đây là một số ứng dụng tiêu biểu của công thức điện trở suất:
- Thiết Kế Và Sản Xuất Dây Dẫn Điện:
Các kỹ sư sử dụng công thức điện trở suất để chọn lựa vật liệu phù hợp khi thiết kế và sản xuất dây dẫn điện. Vật liệu có điện trở suất thấp, như đồng hoặc nhôm, thường được sử dụng để làm dây dẫn trong các hệ thống điện, giúp giảm thiểu tổn thất điện năng.
- Xác Định Vật Liệu Trong Ngành Điện Tử:
Công thức điện trở suất được áp dụng để kiểm tra và xác định các vật liệu sử dụng trong các linh kiện điện tử như điện trở, tụ điện và bán dẫn. Điện trở suất của vật liệu sẽ ảnh hưởng trực tiếp đến hiệu năng và độ bền của các linh kiện này.
- Ứng Dụng Trong Thiết Kế Mạch Điện:
Khi thiết kế mạch điện, các kỹ sư cần tính toán điện trở suất của các vật liệu và các phần tử trong mạch để đảm bảo mạch hoạt động hiệu quả và an toàn. Việc tính toán đúng điện trở suất giúp đảm bảo rằng các phần tử trong mạch không bị quá nhiệt hay hư hỏng do dòng điện.
- Kiểm Tra Và Bảo Trì Hệ Thống Điện:
Trong quá trình kiểm tra và bảo trì các hệ thống điện, kỹ thuật viên sử dụng công thức điện trở suất để đo lường và xác định sự suy giảm của các dây dẫn hoặc thiết bị điện. Điều này giúp phát hiện sớm các vấn đề tiềm ẩn và thực hiện các biện pháp khắc phục kịp thời.
- Nghiên Cứu Vật Liệu Mới:
Các nhà khoa học sử dụng công thức điện trở suất để nghiên cứu và phát triển các vật liệu mới có khả năng dẫn điện tốt hơn, từ đó cải thiện hiệu suất và tính năng của các thiết bị điện tử và hệ thống điện.
Công thức điện trở suất là một công cụ quan trọng trong việc phát triển các ứng dụng công nghệ cao, đóng vai trò then chốt trong việc tối ưu hóa hiệu suất và độ tin cậy của các hệ thống và thiết bị điện tử hiện đại.
XEM THÊM:
5. Sự Phụ Thuộc Của Điện Trở Suất Theo Nhiệt Độ
Điện trở suất của một chất phụ thuộc mạnh mẽ vào nhiệt độ của chất đó. Khi nhiệt độ thay đổi, sự chuyển động của các electron trong vật liệu cũng thay đổi, dẫn đến sự thay đổi điện trở suất.
5.1. Công Thức Phụ Thuộc Nhiệt Độ
Công thức biểu diễn sự phụ thuộc của điện trở suất \( \rho \) theo nhiệt độ \( T \) là:
\[
\rho = \rho_0 \left(1 + \alpha \cdot (T - T_0)\right)
\]
Trong đó:
- \( \rho \): Điện trở suất tại nhiệt độ \( T \) (Ωm)
- \( \rho_0 \): Điện trở suất tại nhiệt độ tham chiếu \( T_0 \) (Ωm)
- \( \alpha \): Hệ số nhiệt điện trở (°C-1)
- \( T \): Nhiệt độ cần tính (°C)
- \( T_0 \): Nhiệt độ tham chiếu, thường là 20°C hoặc 25°C
5.2. Ảnh Hưởng Của Nhiệt Độ Đến Điện Trở Suất
Ảnh hưởng của nhiệt độ đến điện trở suất khác nhau giữa các loại vật liệu:
- Đối với kim loại: Khi nhiệt độ tăng, điện trở suất của kim loại cũng tăng. Điều này là do các ion trong mạng tinh thể kim loại dao động mạnh hơn, cản trở sự di chuyển của các electron, làm tăng điện trở.
- Đối với chất bán dẫn: Điện trở suất của chất bán dẫn giảm khi nhiệt độ tăng. Khi nhiệt độ tăng, nhiều electron có đủ năng lượng để thoát ra khỏi liên kết hóa trị, dẫn đến sự gia tăng số lượng hạt dẫn, làm giảm điện trở suất.
- Đối với vật liệu cách điện: Điện trở suất có thể giảm nhẹ khi nhiệt độ tăng, nhưng nhìn chung sự thay đổi này không đáng kể trừ khi vật liệu tiếp cận điểm nóng chảy hoặc phân hủy nhiệt.
Bằng cách hiểu rõ sự phụ thuộc của điện trở suất theo nhiệt độ, ta có thể ứng dụng vào các bài toán thực tế, như tính toán sự thay đổi điện trở của dây dẫn khi nhiệt độ môi trường thay đổi, hoặc thiết kế các thiết bị điện tử hoạt động ổn định trong các điều kiện nhiệt độ khác nhau.

6. Bài Tập Về Điện Trở Suất
Dưới đây là một số bài tập vận dụng liên quan đến công thức tính điện trở suất, giúp các bạn học sinh củng cố kiến thức và rèn luyện kỹ năng giải bài tập.
6.1. Bài Tập Tính Toán
-
Một dây dẫn bằng đồng có chiều dài \( l = 2 \, m \), tiết diện \( S = 1 \, mm^2 \). Điện trở suất của đồng là \( \rho = 1.7 \times 10^{-8} \, \Omega \cdot m \). Tính điện trở của dây dẫn.
Giải:
Điện trở \( R \) của dây dẫn được tính theo công thức:
\[
R = \frac{\rho \cdot l}{S}
\]Thay số liệu vào công thức:
\[
R = \frac{1.7 \times 10^{-8} \cdot 2}{1 \times 10^{-6}} = 0.034 \, \Omega
\] -
Hai dây dẫn làm từ cùng một loại vật liệu có điện trở suất \( \rho = 2.5 \times 10^{-8} \, \Omega \cdot m \). Dây thứ nhất có chiều dài \( l_1 = 1.5 \, m \) và tiết diện \( S_1 = 0.5 \, mm^2 \), dây thứ hai có chiều dài \( l_2 = 2 \, m \) và tiết diện \( S_2 = 0.8 \, mm^2 \). Tính điện trở của mỗi dây dẫn.
Giải:
Điện trở của dây thứ nhất:
\[
R_1 = \frac{\rho \cdot l_1}{S_1} = \frac{2.5 \times 10^{-8} \cdot 1.5}{0.5 \times 10^{-6}} = 0.075 \, \Omega
\]Điện trở của dây thứ hai:
\[
R_2 = \frac{\rho \cdot l_2}{S_2} = \frac{2.5 \times 10^{-8} \cdot 2}{0.8 \times 10^{-6}} = 0.0625 \, \Omega
\]
6.2. Bài Tập Ứng Dụng Thực Tế
-
Một biến trở có điện trở suất \( \rho = 1.1 \times 10^{-6} \, \Omega \cdot m \), chiều dài dây dẫn là \( l = 20 \, m \), và tiết diện dây dẫn là \( S = 0.5 \, mm^2 \). Tính giá trị lớn nhất của biến trở.
Giải:
Giá trị lớn nhất của biến trở được tính theo công thức:
\[
R_{max} = \frac{\rho \cdot l}{S} = \frac{1.1 \times 10^{-6} \cdot 20}{0.5 \times 10^{-6}} = 44 \, \Omega
\] -
Một dây dẫn làm từ nhôm có điện trở suất \( \rho = 2.8 \times 10^{-8} \, \Omega \cdot m \). Dây có chiều dài \( l = 10 \, m \) và điện trở \( R = 0.28 \, \Omega \). Tính tiết diện của dây dẫn.
Giải:
Tiết diện của dây dẫn được tính theo công thức:
\[
S = \frac{\rho \cdot l}{R} = \frac{2.8 \times 10^{-8} \cdot 10}{0.28} = 1 \times 10^{-6} \, m^2
\]







.jpg)