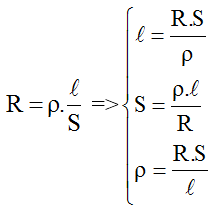Công Thức Tính Điện Trở Toàn Mạch: Hướng Dẫn Chi Tiết và Ứng Dụng Thực Tế

Điện trở là một đại lượng vật lý đặc trưng cho khả năng cản trở dòng điện của vật liệu. Điện trở toàn mạch thường được tính toán dựa trên cách bố trí các điện trở trong mạch, có thể theo dạng nối tiếp, song song hoặc kết hợp cả hai.

Công Thức Tính Điện Trở Toàn Mạch

• Mạch nối tiếp: Trong mạch nối tiếp, các điện trở được nối liền đầu với nhau và dòng điện chỉ có một đường đi. Điện trở toàn mạch \((R_t)\) được tính bằng tổng các điện trở thành phần:

\[
R_t = R_1 + R_2 + R_3 + \ldots + R_n
\]

• Mạch song song: Trong mạch song song, các điện trở được nối sao cho các đầu của chúng kết nối với cùng một điểm chung. Điện trở toàn mạch được tính bằng công thức nghịch đảo của tổng các nghịch đảo điện trở thành phần:

\[
\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}
\]

Do đó:
\[
R_t = \frac{1}{\left(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}\right)}
\]

• Mạch hỗn hợp: Trong mạch hỗn hợp, bao gồm cả các đoạn mạch nối tiếp và song song, chúng ta phải tính điện trở cho từng phần nối tiếp và song song trước, sau đó cộng lại để tìm điện trở toàn mạch.

Ứng Dụng Của Điện Trở Toàn Mạch

Việc tính toán điện trở toàn mạch rất quan trọng trong nhiều ứng dụng thực tế như thiết kế mạch điện, tối ưu hóa tiêu thụ năng lượng trong các thiết bị điện tử, và đảm bảo an toàn trong hệ thống điện. Việc hiểu rõ và áp dụng đúng công thức giúp đảm bảo các thiết bị hoạt động hiệu quả và bền vững.

Kết Luận

Điện trở toàn mạch là một khái niệm cơ bản nhưng rất quan trọng trong lĩnh vực điện tử và kỹ thuật điện. Việc nắm vững các công thức tính toán không chỉ giúp trong việc học tập mà còn trong việc ứng dụng vào thực tế cuộc sống và công việc.

Điện trở là một đại lượng vật lý đặc trưng cho khả năng cản trở dòng điện của một vật liệu hoặc một đoạn mạch. Điện trở càng lớn thì khả năng cản trở dòng điện của vật liệu càng cao. Đơn vị đo của điện trở là Ohm (\(\Omega\)).

Điện trở được ký hiệu bằng chữ cái \(R\) và được xác định bằng công thức cơ bản dựa trên định luật Ohm:

\[
R = \frac{U}{I}
\]

Trong đó:

• \(R\) là điện trở (đo bằng Ohm - \(\Omega\))
• \(U\) là hiệu điện thế đặt vào hai đầu vật dẫn (đo bằng Volt - V)
• \(I\) là cường độ dòng điện chạy qua vật dẫn (đo bằng Ampere - A)

Các vật liệu khác nhau sẽ có điện trở khác nhau, tùy thuộc vào tính chất vật liệu, hình dạng và kích thước của vật dẫn. Một số khái niệm cơ bản liên quan đến điện trở bao gồm:

• Điện trở suất (\(\rho\)): Là một đại lượng đặc trưng cho tính chất vật liệu của một chất dẫn điện. Điện trở suất càng lớn, khả năng dẫn điện của vật liệu càng kém.
• Điện dẫn (\(G\)): Là nghịch đảo của điện trở, đặc trưng cho khả năng dẫn điện của một đoạn mạch.
• Điện trở toàn mạch: Là điện trở tương đương của toàn bộ mạch điện, bao gồm tất cả các điện trở thành phần được nối với nhau theo nhiều cách khác nhau như nối tiếp, song song hoặc hỗn hợp.

Hiểu rõ về điện trở và các khái niệm cơ bản liên quan là nền tảng để tiếp cận các bài toán phức tạp hơn trong điện học, cũng như ứng dụng vào thực tiễn trong thiết kế và vận hành các hệ thống điện.

Trong các mạch điện, việc tính toán điện trở toàn mạch là một bước quan trọng để xác định dòng điện và hiệu điện thế trong mạch. Có ba loại mạch cơ bản mà chúng ta cần xem xét khi tính điện trở toàn mạch: mạch nối tiếp, mạch song song và mạch hỗn hợp.

Mạch Nối Tiếp

Trong mạch nối tiếp, các điện trở được nối liền đầu với nhau, tạo thành một đường duy nhất cho dòng điện chạy qua. Điện trở toàn mạch trong trường hợp này là tổng của tất cả các điện trở thành phần:

\[
R_t = R_1 + R_2 + R_3 + \ldots + R_n
\]

Điều này có nghĩa là nếu bạn có nhiều điện trở nối tiếp nhau, điện trở tổng sẽ tăng lên, làm giảm dòng điện chạy qua mạch.

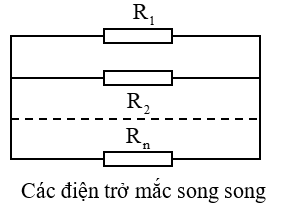
Mạch Song Song

Trong mạch song song, các điện trở được nối sao cho các đầu của chúng được kết nối với cùng một điểm chung, tạo ra nhiều đường cho dòng điện. Điện trở toàn mạch trong trường hợp này được tính bằng cách lấy nghịch đảo của tổng các nghịch đảo của các điện trở thành phần:

\[
\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}
\]

Do đó, điện trở toàn mạch sẽ nhỏ hơn giá trị nhỏ nhất trong các điện trở thành phần. Điều này giúp tăng khả năng dẫn điện của mạch.

Mạch Hỗn Hợp

Mạch hỗn hợp là sự kết hợp của cả mạch nối tiếp và mạch song song. Để tính điện trở toàn mạch trong trường hợp này, bạn cần thực hiện từng bước:

1. Tính điện trở tương đương cho từng phần mạch nối tiếp và song song.
2. Kết hợp các điện trở tương đương để tìm điện trở tổng của mạch.

Ví dụ, nếu bạn có một mạch bao gồm hai điện trở nối tiếp \(R_1\) và \(R_2\), kết nối song song với một điện trở \(R_3\), bạn sẽ tính như sau:

\[
R_{song \, song} = \frac{1}{\left(\frac{1}{R_1 + R_2} + \frac{1}{R_3}\right)}
\]

Hiểu rõ cách tính điện trở toàn mạch trong các loại mạch khác nhau sẽ giúp bạn phân tích và thiết kế các mạch điện một cách hiệu quả hơn.

Để hiểu rõ hơn về cách tính điện trở toàn mạch, chúng ta sẽ cùng xem qua một số ví dụ cụ thể dưới đây. Các ví dụ này sẽ giúp bạn nắm vững phương pháp tính toán trong các loại mạch khác nhau.

Ví dụ 1: Mạch Nối Tiếp

Giả sử bạn có một mạch gồm ba điện trở nối tiếp, với các giá trị lần lượt là \(R_1 = 10 \, \Omega\), \(R_2 = 20 \, \Omega\), và \(R_3 = 30 \, \Omega\). Hãy tính điện trở toàn mạch.

Bước 1: Sử dụng công thức tính điện trở trong mạch nối tiếp:

\[
R_t = R_1 + R_2 + R_3
\]

Bước 2: Thay các giá trị đã biết vào công thức:

\[
R_t = 10 \, \Omega + 20 \, \Omega + 30 \, \Omega = 60 \, \Omega
\]

Vậy, điện trở toàn mạch trong trường hợp này là \(60 \, \Omega\).

Ví dụ 2: Mạch Song Song

Xét một mạch gồm ba điện trở song song với các giá trị lần lượt là \(R_1 = 10 \, \Omega\), \(R_2 = 20 \, \Omega\), và \(R_3 = 30 \, \Omega\). Hãy tính điện trở toàn mạch.

Bước 1: Sử dụng công thức tính điện trở trong mạch song song:

\[
\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\]

Bước 2: Thay các giá trị đã biết vào công thức:

\[
\frac{1}{R_t} = \frac{1}{10 \, \Omega} + \frac{1}{20 \, \Omega} + \frac{1}{30 \, \Omega}
\]

Bước 3: Tính toán giá trị nghịch đảo của tổng các nghịch đảo:

\[
\frac{1}{R_t} = 0.1 + 0.05 + 0.0333 = 0.1833
\]

Bước 4: Lấy nghịch đảo của kết quả trên để tìm \(R_t\):

\[
R_t = \frac{1}{0.1833} \approx 5.45 \, \Omega
\]

Vậy, điện trở toàn mạch trong trường hợp này là khoảng \(5.45 \, \Omega\).

Ví dụ 3: Mạch Hỗn Hợp

Giả sử bạn có một mạch hỗn hợp gồm hai điện trở \(R_1 = 10 \, \Omega\) và \(R_2 = 20 \, \Omega\) nối tiếp với nhau, rồi song song với một điện trở \(R_3 = 30 \, \Omega\). Hãy tính điện trở toàn mạch.

Bước 1: Tính điện trở của phần mạch nối tiếp:

\[
R_{series} = R_1 + R_2 = 10 \, \Omega + 20 \, \Omega = 30 \, \Omega
\]

Bước 2: Tính điện trở tổng của mạch bằng cách kết hợp \(R_{series}\) với \(R_3\) trong mạch song song:

\[
\frac{1}{R_t} = \frac{1}{R_{series}} + \frac{1}{R_3} = \frac{1}{30 \, \Omega} + \frac{1}{30 \, \Omega} = \frac{2}{30 \, \Omega}
\]

Bước 3: Lấy nghịch đảo của kết quả trên để tìm \(R_t\):

\[
R_t = \frac{30 \, \Omega}{2} = 15 \, \Omega
\]

Vậy, điện trở toàn mạch trong trường hợp này là \(15 \, \Omega\).

Điện trở là một trong những linh kiện quan trọng và phổ biến nhất trong các mạch điện và điện tử. Dưới đây là một số ứng dụng thực tế của điện trở trong mạch điện:

1. Điều chỉnh dòng điện

Điện trở được sử dụng để điều chỉnh dòng điện trong mạch. Bằng cách thay đổi giá trị của điện trở, ta có thể kiểm soát dòng điện đi qua các phần khác nhau của mạch. Điều này rất quan trọng trong việc bảo vệ các linh kiện điện tử khỏi bị quá tải và hư hỏng.

2. Chia điện áp

Điện trở thường được sử dụng trong các mạch chia điện áp để tạo ra các mức điện áp khác nhau từ một nguồn điện duy nhất. Mạch chia điện áp cơ bản bao gồm hai điện trở nối tiếp:

\[
V_{out} = V_{in} \times \frac{R_2}{R_1 + R_2}
\]

Trong đó \(V_{in}\) là điện áp đầu vào, \(V_{out}\) là điện áp đầu ra, và \(R_1\), \(R_2\) là các điện trở.

3. Tạo dòng điện ổn định

Trong một số mạch điện, điện trở được sử dụng để tạo ra một dòng điện ổn định cho các linh kiện nhạy cảm như diode, LED, hoặc transistor. Điều này giúp các linh kiện hoạt động ổn định và hiệu quả.

4. Lọc tín hiệu

Điện trở cùng với tụ điện được sử dụng trong các mạch lọc để loại bỏ các thành phần tần số không mong muốn từ tín hiệu. Các mạch lọc thông thấp, thông cao, và thông dải đều sử dụng điện trở trong cấu trúc của chúng.

5. Phát hiện và cảm biến

Điện trở có thể được sử dụng trong các mạch cảm biến để phát hiện các điều kiện môi trường như nhiệt độ, ánh sáng, và độ ẩm. Các cảm biến nhiệt độ, chẳng hạn như nhiệt điện trở, thay đổi giá trị điện trở dựa trên nhiệt độ môi trường.

6. Bảo vệ mạch

Điện trở được sử dụng trong các mạch bảo vệ để giới hạn dòng điện nhằm ngăn ngừa sự cố và hư hỏng cho các thiết bị khác trong mạch. Chúng có thể được sử dụng cùng với cầu chì để đảm bảo an toàn cho mạch điện.

Các ứng dụng của điện trở trong thực tế rất đa dạng, và hiểu rõ vai trò của chúng sẽ giúp bạn thiết kế và sử dụng mạch điện một cách hiệu quả và an toàn.

Khi tính toán điện trở toàn mạch, có một số điểm quan trọng cần lưu ý để đảm bảo kết quả chính xác và tránh các sai sót thường gặp. Dưới đây là các lưu ý chính mà bạn cần xem xét:

1. Xác định đúng loại mạch

Trước khi bắt đầu tính toán, bạn cần xác định loại mạch mà mình đang làm việc là mạch nối tiếp, mạch song song hay mạch hỗn hợp. Mỗi loại mạch có phương pháp tính điện trở toàn mạch khác nhau:

• Trong mạch nối tiếp, tổng điện trở bằng tổng các điện trở thành phần.
• Trong mạch song song, điện trở toàn mạch được tính bằng tổng nghịch đảo các điện trở thành phần.
• Trong mạch hỗn hợp, bạn cần tính từng phần mạch nối tiếp hoặc song song trước khi tổng hợp lại.

2. Chú ý đến giá trị điện trở

Khi thực hiện các phép tính, hãy chắc chắn rằng bạn sử dụng đúng giá trị điện trở, bao gồm đơn vị đo lường. Điện trở thường được đo bằng Ohm (\(\Omega\)), nhưng cũng có thể gặp các giá trị lớn hơn như kilo-Ohm (k\(\Omega\)) hoặc mega-Ohm (M\(\Omega\)). Việc sai sót trong đơn vị có thể dẫn đến kết quả không chính xác.

3. Kiểm tra kỹ các kết nối trong mạch

Trước khi tính toán, hãy kiểm tra lại các kết nối trong mạch để đảm bảo rằng không có sai sót nào. Ví dụ, một điện trở bị kết nối sai có thể làm thay đổi loại mạch từ song song sang nối tiếp, dẫn đến kết quả sai lệch.

4. Sử dụng đúng công cụ và công thức

Đảm bảo rằng bạn sử dụng đúng công cụ và công thức để tính toán. Nếu bạn đang tính toán thủ công, hãy sử dụng máy tính bỏ túi có độ chính xác cao. Trong một số trường hợp, sử dụng phần mềm mô phỏng mạch điện cũng có thể giúp bạn xác nhận lại kết quả của mình.

5. Kiểm tra kết quả cuối cùng

Sau khi hoàn thành tính toán, hãy kiểm tra lại kết quả cuối cùng. Đảm bảo rằng điện trở toàn mạch có giá trị hợp lý dựa trên các điện trở thành phần. Nếu kết quả có vẻ không đúng, hãy kiểm tra lại từng bước để tìm ra lỗi.

6. Hiểu rõ mạch điện trước khi tiến hành tính toán

Cuối cùng, việc hiểu rõ cách thức hoạt động của mạch điện sẽ giúp bạn tính toán điện trở toàn mạch chính xác hơn. Đôi khi, chỉ cần một sự thay đổi nhỏ trong cấu trúc mạch cũng có thể ảnh hưởng lớn đến kết quả, do đó việc nắm vững kiến thức cơ bản là rất cần thiết.

Việc nắm vững các lưu ý trên sẽ giúp bạn tính toán điện trở toàn mạch một cách chính xác, tránh được những sai sót thường gặp và đảm bảo hiệu quả của mạch điện trong thực tế.

Điện trở toàn mạch đóng vai trò vô cùng quan trọng trong việc đảm bảo hiệu suất và an toàn của các mạch điện. Bằng cách tính toán chính xác điện trở toàn mạch, chúng ta có thể điều chỉnh dòng điện và điện áp phù hợp với yêu cầu của các thiết bị điện tử, tránh hiện tượng quá tải hoặc hư hỏng linh kiện.

Việc hiểu rõ và áp dụng đúng công thức tính điện trở toàn mạch không chỉ giúp tăng cường hiệu quả hoạt động của mạch điện mà còn là nền tảng cơ bản trong việc thiết kế và triển khai các hệ thống điện tử phức tạp. Đặc biệt, trong các ứng dụng thực tế như điều khiển, cảm biến và bảo vệ mạch, điện trở toàn mạch góp phần quan trọng trong việc ổn định và tối ưu hóa các thông số kỹ thuật của hệ thống.

Hơn nữa, sự nhận thức đúng về tầm quan trọng của điện trở toàn mạch sẽ giúp người học và các kỹ sư điện tử nâng cao kỹ năng phân tích mạch, từ đó có thể ứng dụng hiệu quả trong công việc và nghiên cứu. Sự chính xác trong các phép tính không chỉ mang lại kết quả chính xác mà còn góp phần vào sự phát triển bền vững của các hệ thống điện và điện tử trong thực tế.

Tóm lại, điện trở toàn mạch là một thành phần không thể thiếu, đóng vai trò chủ chốt trong việc bảo đảm hoạt động ổn định và an toàn cho các mạch điện. Việc nắm vững kiến thức về điện trở toàn mạch là một yếu tố quan trọng giúp nâng cao hiệu suất và độ tin cậy của mọi hệ thống điện tử.