Chủ đề viết công thức tính điện trở của dây dẫn: Viết công thức tính điện trở của dây dẫn là một phần quan trọng trong việc thiết kế và xây dựng các hệ thống điện. Bài viết này cung cấp hướng dẫn chi tiết về cách viết công thức, các yếu tố ảnh hưởng đến điện trở, và ứng dụng thực tế trong kỹ thuật điện tử. Đọc tiếp để khám phá kiến thức cần thiết để tính toán và tối ưu hóa điện trở trong các dự án của bạn.
Mục lục
Công Thức Tính Điện Trở Của Dây Dẫn
Điện trở của một dây dẫn là đại lượng thể hiện khả năng cản trở dòng điện chạy qua nó. Để tính toán điện trở của một dây dẫn, ta sử dụng công thức sau:
\[ R = \frac{\rho \cdot L}{S} \]
- R: Điện trở của dây dẫn, đơn vị đo là Ohm (Ω).
- L: Chiều dài của dây dẫn, đơn vị đo là mét (m).
- S: Tiết diện ngang của dây dẫn, đơn vị đo là mét vuông (m²).
- ρ (rho): Điện trở suất của vật liệu làm dây dẫn, đơn vị đo là Ohm mét (Ω·m).
Điện Trở Suất Của Vật Liệu
Điện trở suất (\(\rho\)) là một đặc tính vật lý quan trọng của vật liệu dùng để làm dây dẫn, thể hiện mức độ cản trở dòng điện của vật liệu đó. Điện trở suất phụ thuộc vào loại vật liệu và nhiệt độ của nó. Các vật liệu như đồng có điện trở suất thấp, trong khi nhựa có điện trở suất cao.
Các Yếu Tố Ảnh Hưởng Đến Điện Trở Của Dây Dẫn
Điện trở của dây dẫn phụ thuộc vào các yếu tố sau:
- Chiều dài dây dẫn (L): Điện trở tỷ lệ thuận với chiều dài của dây. Dây dẫn dài hơn sẽ có điện trở cao hơn.
- Tiết diện dây dẫn (S): Điện trở tỷ lệ nghịch với tiết diện của dây. Dây dẫn có tiết diện lớn hơn sẽ có điện trở thấp hơn.
- Vật liệu làm dây dẫn (ρ): Điện trở của dây phụ thuộc vào vật liệu cấu thành. Vật liệu có điện trở suất cao sẽ tạo ra điện trở lớn hơn.
Ứng Dụng Của Công Thức Tính Điện Trở Trong Thực Tế
Công thức tính điện trở được áp dụng rộng rãi trong nhiều lĩnh vực như thiết kế mạch điện, đo lường điện trở, kiểm tra chất lượng dây dẫn, và tính toán sức chịu tải của dây dẫn trong các hệ thống điện. Hiểu rõ về điện trở suất và cách tính điện trở giúp kỹ sư và nhà thiết kế lựa chọn vật liệu và thiết kế hệ thống điện hiệu quả và an toàn.
Ví Dụ Bài Tập Tính Điện Trở
Dưới đây là một ví dụ cụ thể để minh họa cách sử dụng công thức tính điện trở:
Ví dụ: Tính điện trở của một dây dẫn bằng đồng có chiều dài 100m, tiết diện ngang là 1 mm² và điện trở suất của đồng là \(1.68 \times 10^{-8} \Omega\cdot m\).
Lời giải:
Áp dụng công thức:
\[ R = \frac{1.68 \times 10^{-8} \cdot 100}{1 \times 10^{-6}} = 0.168 \Omega \]
Vậy điện trở của dây dẫn này là 0.168 Ω.
Kết Luận
Công thức tính điện trở của dây dẫn là công cụ cơ bản và quan trọng trong lĩnh vực điện và điện tử, giúp đảm bảo các hệ thống điện hoạt động hiệu quả và an toàn. Việc nắm vững công thức này là cần thiết cho việc thiết kế, lắp đặt, và kiểm tra các hệ thống điện trong thực tế.
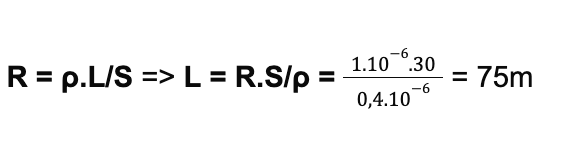
.png)
1. Khái Niệm Về Điện Trở Của Dây Dẫn
Điện trở của dây dẫn là một đại lượng vật lý biểu thị khả năng cản trở dòng điện của dây dẫn đó. Điện trở được ký hiệu là \( R \) và được đo bằng đơn vị Ohm (Ω). Để hiểu rõ hơn, chúng ta cần xem xét các yếu tố cơ bản cấu thành điện trở của một dây dẫn.
- Điện trở suất (\( \rho \)): Đây là đặc tính của vật liệu làm dây dẫn, biểu thị khả năng cản trở dòng điện của vật liệu đó. Điện trở suất có đơn vị là Ohm mét (\( \Omega \cdot m \)). Vật liệu có điện trở suất cao sẽ có điện trở lớn.
- Chiều dài dây dẫn (\( L \)): Điện trở của dây dẫn tỷ lệ thuận với chiều dài của nó. Dây dẫn càng dài thì điện trở càng lớn.
- Tiết diện ngang của dây dẫn (\( S \)): Điện trở tỷ lệ nghịch với tiết diện của dây dẫn. Dây dẫn có tiết diện lớn sẽ có điện trở nhỏ hơn.
Công thức tính điện trở của dây dẫn được biểu diễn như sau:
\[ R = \frac{\rho \cdot L}{S} \]
Trong đó:
- \( R \): Điện trở của dây dẫn (Ω).
- \( \rho \): Điện trở suất của vật liệu (Ω·m).
- \( L \): Chiều dài dây dẫn (m).
- \( S \): Tiết diện ngang của dây dẫn (m²).
Điện trở của dây dẫn có vai trò quan trọng trong việc xác định hiệu quả truyền tải điện năng và an toàn của hệ thống điện. Hiểu rõ khái niệm này giúp tối ưu hóa thiết kế mạch điện và lựa chọn vật liệu phù hợp.
2. Công Thức Tính Điện Trở Dây Dẫn
Công thức tính điện trở của dây dẫn là một công cụ quan trọng trong lĩnh vực điện và điện tử, giúp xác định khả năng cản trở dòng điện của dây dẫn. Điện trở của một dây dẫn có thể được tính thông qua công thức:
\[ R = \frac{\rho \cdot L}{S} \]
Trong đó:
- \( R \) là điện trở của dây dẫn, được đo bằng Ohm (Ω).
- \( \rho \) là điện trở suất của vật liệu làm dây dẫn, đơn vị là Ohm mét (\( \Omega \cdot m \)).
- \( L \) là chiều dài của dây dẫn, đơn vị là mét (m).
- \( S \) là tiết diện ngang của dây dẫn, đơn vị là mét vuông (\( m^2 \)).
Điện trở suất (\( \rho \)) là một thông số đặc trưng cho mỗi loại vật liệu và ảnh hưởng trực tiếp đến giá trị điện trở của dây dẫn. Ví dụ, đồng có điện trở suất thấp, trong khi nhôm có điện trở suất cao hơn, dẫn đến điện trở của dây dẫn nhôm lớn hơn so với dây dẫn bằng đồng cùng kích thước.
Để hiểu rõ hơn, chúng ta có thể áp dụng công thức trên trong một ví dụ cụ thể. Giả sử chúng ta có một dây dẫn bằng đồng với các thông số như sau:
- Chiều dài dây dẫn \( L = 100 \, m \)
- Tiết diện ngang \( S = 1 \, mm^2 = 1 \times 10^{-6} \, m^2 \)
- Điện trở suất của đồng \( \rho = 1.68 \times 10^{-8} \, \Omega \cdot m \)
Áp dụng công thức tính điện trở:
\[ R = \frac{1.68 \times 10^{-8} \cdot 100}{1 \times 10^{-6}} = 1.68 \, \Omega \]
Vậy điện trở của dây dẫn này là \( 1.68 \, \Omega \).
Thông qua công thức này, các kỹ sư và nhà thiết kế có thể tính toán và tối ưu hóa thiết kế dây dẫn, đảm bảo hiệu quả truyền tải điện năng và an toàn trong các hệ thống điện.

3. Điện Trở Suất Của Vật Liệu
Điện trở suất (\(\rho\)) là một đặc tính vật lý quan trọng của vật liệu, xác định khả năng cản trở dòng điện của vật liệu đó. Điện trở suất được đo bằng đơn vị Ohm mét (\(\Omega \cdot m\)). Mỗi loại vật liệu khác nhau sẽ có giá trị điện trở suất khác nhau, ảnh hưởng trực tiếp đến điện trở của dây dẫn.
3.1. Ý Nghĩa Của Điện Trở Suất
Điện trở suất cho biết mức độ dễ hay khó mà dòng điện có thể đi qua vật liệu. Vật liệu có điện trở suất thấp sẽ dẫn điện tốt hơn và ngược lại. Ví dụ, kim loại như đồng và nhôm có điện trở suất thấp, do đó chúng thường được sử dụng làm dây dẫn điện trong các hệ thống điện.
3.2. Các Yếu Tố Ảnh Hưởng Đến Điện Trở Suất
Điện trở suất của một vật liệu có thể thay đổi phụ thuộc vào một số yếu tố:
- Nhiệt độ: Điện trở suất của hầu hết các vật liệu sẽ tăng lên khi nhiệt độ tăng. Đối với kim loại, sự gia tăng nhiệt độ làm tăng sự chuyển động nhiệt của các electron, gây ra nhiều va chạm hơn và do đó tăng điện trở suất.
- Loại vật liệu: Mỗi vật liệu có cấu trúc nguyên tử khác nhau, dẫn đến sự khác biệt trong điện trở suất. Ví dụ, đồng (\(\rho = 1.68 \times 10^{-8} \, \Omega \cdot m\)) có điện trở suất thấp hơn so với sắt (\(\rho = 9.71 \times 10^{-8} \, \Omega \cdot m\)).
- Trạng thái tinh khiết: Tạp chất và khuyết tật trong vật liệu có thể làm tăng điện trở suất do chúng cản trở chuyển động của electron.
3.3. Bảng Giá Trị Điện Trở Suất Của Một Số Vật Liệu Thường Gặp
| Vật Liệu | Điện Trở Suất (\(\Omega \cdot m\)) |
|---|---|
| Đồng | \(1.68 \times 10^{-8}\) |
| Nhôm | \(2.82 \times 10^{-8}\) |
| Sắt | \(9.71 \times 10^{-8}\) |
| Vàng | \(2.44 \times 10^{-8}\) |
| Chì | \(2.20 \times 10^{-7}\) |
3.4. Ứng Dụng Thực Tế Của Điện Trở Suất
Việc lựa chọn vật liệu với điện trở suất phù hợp là rất quan trọng trong thiết kế hệ thống điện. Ví dụ, đồng thường được chọn làm dây dẫn chính trong các mạch điện do điện trở suất thấp, giúp giảm thiểu tổn hao năng lượng. Trong các ứng dụng đặc biệt, như mạch điện trong môi trường nhiệt độ cao, vật liệu với điện trở suất cao hơn có thể được sử dụng để kiểm soát nhiệt lượng sinh ra.
Hiểu rõ về điện trở suất của vật liệu giúp các kỹ sư và nhà thiết kế tối ưu hóa hiệu suất của hệ thống điện, đồng thời đảm bảo an toàn và hiệu quả kinh tế trong việc sử dụng vật liệu.

4. Ứng Dụng Của Công Thức Tính Điện Trở
Công thức tính điện trở của dây dẫn không chỉ là một công cụ lý thuyết mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau. Việc sử dụng công thức này giúp các kỹ sư, nhà thiết kế, và nhà nghiên cứu đảm bảo tính chính xác trong thiết kế và vận hành các hệ thống điện. Dưới đây là một số ứng dụng quan trọng của công thức tính điện trở.
4.1. Thiết Kế Mạch Điện
Trong quá trình thiết kế mạch điện, công thức tính điện trở được sử dụng để lựa chọn vật liệu và kích thước dây dẫn phù hợp nhằm đảm bảo hiệu quả truyền tải điện năng và an toàn cho hệ thống. Việc tính toán chính xác điện trở giúp hạn chế tổn hao năng lượng, đảm bảo điện áp đến các thiết bị được ổn định.
4.2. Đo Lường và Kiểm Tra Chất Lượng Dây Dẫn
Các nhà sản xuất và kỹ sư sử dụng công thức tính điện trở để kiểm tra chất lượng dây dẫn trong quá trình sản xuất. Bằng cách đo điện trở của dây dẫn, có thể đánh giá được chất lượng vật liệu và đảm bảo rằng sản phẩm đáp ứng các tiêu chuẩn kỹ thuật cần thiết.
4.3. Tính Toán Sức Chịu Tải và Đảm Bảo An Toàn Hệ Thống
Trong các hệ thống điện, việc tính toán điện trở giúp xác định sức chịu tải của dây dẫn và đảm bảo rằng dây dẫn không bị quá tải, gây ra hiện tượng nóng chảy hoặc cháy nổ. Công thức tính điện trở cho phép tính toán chính xác dòng điện tối đa mà dây dẫn có thể chịu được mà không gây ra hư hỏng.
4.4. Ứng Dụng Trong Các Thiết Bị Điện Tử
Điện trở là một thành phần quan trọng trong các mạch điện tử. Bằng cách tính toán điện trở của dây dẫn và các linh kiện, các kỹ sư có thể điều chỉnh dòng điện và điện áp trong mạch để đạt được các thông số hoạt động mong muốn. Điều này đặc biệt quan trọng trong các thiết bị điện tử chính xác, như máy tính và thiết bị y tế.
4.5. Quản Lý Năng Lượng Trong Hệ Thống Điện
Trong các hệ thống quản lý năng lượng, việc tính toán điện trở của dây dẫn giúp tối ưu hóa việc phân phối điện năng và giảm thiểu tổn thất điện năng. Điều này đóng vai trò quan trọng trong việc nâng cao hiệu quả sử dụng năng lượng và giảm chi phí vận hành cho các hệ thống điện quy mô lớn.
Như vậy, công thức tính điện trở không chỉ là một công cụ lý thuyết mà còn có nhiều ứng dụng thực tiễn quan trọng, giúp nâng cao hiệu quả, an toàn và độ tin cậy của các hệ thống điện trong đời sống và công nghiệp.

5. Ví Dụ Thực Tế Về Tính Điện Trở
Để minh họa cho việc áp dụng công thức tính điện trở trong thực tế, chúng ta sẽ xem xét một vài ví dụ cụ thể. Những ví dụ này sẽ giúp bạn hiểu rõ hơn về cách tính toán và ứng dụng công thức trong các trường hợp khác nhau.
5.1. Ví Dụ 1: Tính Điện Trở Của Dây Dẫn Đồng
Giả sử chúng ta có một dây dẫn bằng đồng với các thông số sau:
- Chiều dài dây dẫn \(L = 200 \, m\)
- Tiết diện ngang của dây \(S = 2 \, mm^2 = 2 \times 10^{-6} \, m^2\)
- Điện trở suất của đồng \(\rho = 1.68 \times 10^{-8} \, \Omega \cdot m\)
Áp dụng công thức tính điện trở:
\[ R = \frac{\rho \cdot L}{S} = \frac{1.68 \times 10^{-8} \cdot 200}{2 \times 10^{-6}} = 1.68 \, \Omega \]
Vậy, điện trở của dây dẫn này là \(1.68 \, \Omega\).
5.2. Ví Dụ 2: Tính Điện Trở Của Dây Nhôm
Xét một dây dẫn làm từ nhôm với các thông số như sau:
- Chiều dài dây dẫn \(L = 500 \, m\)
- Tiết diện ngang của dây \(S = 1.5 \, mm^2 = 1.5 \times 10^{-6} \, m^2\)
- Điện trở suất của nhôm \(\rho = 2.82 \times 10^{-8} \, \Omega \cdot m\)
Tính toán điện trở:
\[ R = \frac{\rho \cdot L}{S} = \frac{2.82 \times 10^{-8} \cdot 500}{1.5 \times 10^{-6}} = 9.4 \, \Omega \]
Như vậy, điện trở của dây dẫn nhôm là \(9.4 \, \Omega\).
5.3. Ví Dụ 3: Ứng Dụng Trong Thực Tế
Trong một hệ thống điện gia đình, dây dẫn điện được lựa chọn dựa trên việc tính toán điện trở để đảm bảo rằng dây dẫn có thể chịu được dòng điện cần thiết mà không gây quá tải. Giả sử bạn cần truyền tải một dòng điện 10A qua một dây dẫn có chiều dài 100m, sử dụng dây dẫn bằng đồng có tiết diện 2mm². Ta sẽ tính toán xem liệu dây dẫn này có phù hợp hay không.
Với các thông số sau:
- Chiều dài dây dẫn \(L = 100 \, m\)
- Tiết diện ngang của dây \(S = 2 \, mm^2 = 2 \times 10^{-6} \, m^2\)
- Điện trở suất của đồng \(\rho = 1.68 \times 10^{-8} \, \Omega \cdot m\)
Tính toán điện trở:
\[ R = \frac{1.68 \times 10^{-8} \cdot 100}{2 \times 10^{-6}} = 0.84 \, \Omega \]
Với điện trở này, tổng điện áp rơi trên dây dẫn khi có dòng điện 10A là:
\[ U = I \cdot R = 10 \times 0.84 = 8.4 \, V \]
Điều này có nghĩa là khi truyền tải điện qua dây dẫn này, có một tổn thất điện áp 8.4V, điều này có thể chấp nhận được trong một số trường hợp, nhưng cũng cần cân nhắc thêm để tối ưu hóa hệ thống.
Những ví dụ này minh họa cách công thức tính điện trở được áp dụng trong thực tế để đảm bảo hiệu quả và an toàn trong các hệ thống điện.
XEM THÊM:
6. Kết Luận
Trong lĩnh vực kỹ thuật điện, việc nắm vững công thức tính điện trở của dây dẫn là vô cùng quan trọng. Nó không chỉ giúp người học hiểu rõ hơn về các nguyên lý cơ bản của dòng điện mà còn hỗ trợ trong việc thiết kế và xây dựng các hệ thống điện hiệu quả và an toàn.
Công thức tính điện trở của dây dẫn được thể hiện như sau:
\[ R = \rho \cdot \frac{L}{S} \]
Trong đó:
- \(R\) là điện trở của dây dẫn (đơn vị: Ohm, \( \Omega \)).
- \(\rho\) là điện trở suất của vật liệu làm dây dẫn (đơn vị: Ohm mét, \( \Omega \cdot m \)).
- \(L\) là chiều dài của dây dẫn (đơn vị: mét, \( m \)).
- \(S\) là tiết diện ngang của dây dẫn (đơn vị: mét vuông, \( m^2 \)).
Qua công thức trên, ta thấy rằng điện trở của dây dẫn phụ thuộc chặt chẽ vào các yếu tố như vật liệu cấu thành, chiều dài, và tiết diện của dây dẫn. Do đó, trong thực tiễn, việc lựa chọn đúng loại dây dẫn với các thông số phù hợp là rất quan trọng để đảm bảo hiệu suất và an toàn của hệ thống điện.
Đối với các kỹ sư và nhà thiết kế, việc hiểu rõ và áp dụng đúng công thức tính điện trở sẽ giúp họ tối ưu hóa thiết kế, từ đó tiết kiệm chi phí và nâng cao độ tin cậy của các công trình điện. Đồng thời, trong quá trình sản xuất và kiểm tra chất lượng dây dẫn, việc đo lường chính xác điện trở sẽ giúp đảm bảo rằng sản phẩm đạt được các tiêu chuẩn kỹ thuật cần thiết.
Cuối cùng, chúng ta nên nhớ rằng công thức tính điện trở không chỉ là một công cụ lý thuyết mà còn là một phần thiết yếu trong quá trình thực hiện các dự án thực tế. Việc nắm vững và vận dụng thành thạo công thức này sẽ mang lại nhiều lợi ích thiết thực, góp phần vào sự thành công của mọi dự án điện.




.png)




