Chủ đề công thức tính điện trở lớp 9: Công thức tính điện trở lớp 9 không chỉ là nền tảng quan trọng trong môn Vật Lý, mà còn là kiến thức hữu ích trong đời sống và công nghiệp. Bài viết này sẽ hướng dẫn chi tiết cách tính điện trở, giải thích các yếu tố ảnh hưởng và ứng dụng thực tế, giúp học sinh nắm vững lý thuyết và tự tin áp dụng vào thực tế.
Mục lục
Công Thức Tính Điện Trở - Lớp 9
Điện trở là một khái niệm quan trọng trong vật lý, đặc biệt là trong điện học. Công thức tính điện trở giúp học sinh hiểu rõ hơn về mối quan hệ giữa điện áp, cường độ dòng điện và điện trở trong mạch điện.
1. Công thức tính điện trở:
Điện trở được tính bằng công thức:
\[
R = \frac{U}{I}
\]
Trong đó:
- \(R\) là điện trở (đơn vị: Ohm, ký hiệu: \(\Omega\))
- \(U\) là điện áp đặt vào hai đầu của điện trở (đơn vị: Vôn, ký hiệu: V)
- \(I\) là cường độ dòng điện chạy qua điện trở (đơn vị: Ampe, ký hiệu: A)
2. Định luật Ôm:
Định luật Ôm phát biểu rằng: "Cường độ dòng điện chạy qua một dây dẫn tỉ lệ thuận với hiệu điện thế giữa hai đầu dây dẫn và tỉ lệ nghịch với điện trở của dây dẫn đó". Công thức của định luật Ôm là:
\[
I = \frac{U}{R}
\]
Từ công thức này, ta có thể dễ dàng suy ra công thức tính điện trở \(R\) như trên.
3. Ứng dụng trong thực tế:
Công thức tính điện trở và định luật Ôm được ứng dụng rộng rãi trong thực tế, từ việc thiết kế mạch điện, đo lường điện trở cho đến việc phân tích các hiện tượng điện học trong nhiều lĩnh vực khác nhau.
4. Bài tập minh họa:
Hãy giải bài toán sau để củng cố kiến thức:
Cho một mạch điện với điện áp \(U = 12V\) và cường độ dòng điện \(I = 2A\). Tính điện trở của mạch.
Lời giải:
Áp dụng công thức tính điện trở:
\[
R = \frac{U}{I} = \frac{12V}{2A} = 6 \Omega
\]
Vậy điện trở của mạch là \(6 \Omega\).
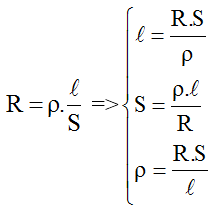
.png)
1. Khái Niệm Cơ Bản Về Điện Trở
Điện trở là một đại lượng vật lý biểu thị sự cản trở dòng điện của một vật liệu. Khi có dòng điện chạy qua một dây dẫn, các electron sẽ va chạm với các nguyên tử trong dây dẫn, gây ra sự cản trở và làm giảm cường độ dòng điện. Đại lượng này được gọi là điện trở, ký hiệu là \(R\), và đơn vị đo là ohm (Ω).
Điện trở phụ thuộc vào nhiều yếu tố, bao gồm:
- Vật liệu dây dẫn: Mỗi vật liệu có điện trở suất khác nhau. Chất liệu như đồng có điện trở suất thấp, trong khi chất liệu như cao su có điện trở suất cao.
- Chiều dài dây dẫn: Điện trở tỉ lệ thuận với chiều dài của dây dẫn. Dây càng dài thì điện trở càng lớn.
- Diện tích tiết diện: Điện trở tỉ lệ nghịch với diện tích tiết diện của dây dẫn. Tiết diện càng lớn, điện trở càng nhỏ.
- Nhiệt độ: Nhiệt độ càng cao thì điện trở của dây dẫn càng tăng.
Công thức tính điện trở được biểu diễn qua công thức:
\[
R = \frac{\rho \cdot l}{S}
\]
Trong đó:
- \(R\) là điện trở (Ω)
- \(\rho\) là điện trở suất của vật liệu (Ω.m)
- \(l\) là chiều dài của dây dẫn (m)
- \(S\) là diện tích tiết diện của dây dẫn (m²)
Hiểu rõ khái niệm điện trở và các yếu tố ảnh hưởng đến nó giúp chúng ta có thể áp dụng vào thực tế, như trong thiết kế mạch điện hay tính toán hiệu quả sử dụng năng lượng.
2. Công Thức Tính Điện Trở
Công thức tính điện trở là một phần quan trọng trong môn Vật Lý lớp 9, giúp học sinh hiểu rõ cách xác định điện trở của một dây dẫn trong mạch điện. Điện trở của một dây dẫn được tính theo công thức:
\[
R = \frac{\rho \cdot l}{S}
\]
Trong đó:
- \(\rho\) (rho) là điện trở suất của vật liệu làm dây dẫn, đơn vị là \(\Omega \cdot m\). Mỗi vật liệu có giá trị điện trở suất khác nhau; ví dụ, đồng có điện trở suất thấp hơn so với sắt.
- \(l\) là chiều dài của dây dẫn, đơn vị là mét (m). Chiều dài dây dẫn càng lớn thì điện trở của dây càng cao.
- \(S\) là diện tích tiết diện ngang của dây dẫn, đơn vị là mét vuông (m²). Tiết diện càng lớn thì điện trở càng nhỏ.
Để hiểu rõ hơn về cách áp dụng công thức này, hãy xem xét một ví dụ cụ thể:
- Giả sử chúng ta có một dây dẫn bằng đồng với chiều dài \(l = 100 \, m\), diện tích tiết diện \(S = 1 \, mm^2\) và điện trở suất của đồng là \(\rho = 1.68 \times 10^{-8} \, \Omega \cdot m\).
- Thay các giá trị vào công thức, ta có: \[ R = \frac{1.68 \times 10^{-8} \times 100}{1 \times 10^{-6}} = 1.68 \, \Omega \]
- Kết quả, điện trở của dây dẫn là \(1.68 \, \Omega\).
Việc nắm vững công thức này sẽ giúp các bạn học sinh dễ dàng tính toán điện trở trong các bài tập thực tế và trong các bài kiểm tra.

3. Ứng Dụng Của Điện Trở Trong Đời Sống
Điện trở không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và công nghiệp. Dưới đây là một số ứng dụng tiêu biểu:
- Thiết bị điện tử: Điện trở được sử dụng rộng rãi trong các mạch điện tử để điều chỉnh dòng điện và điện áp. Trong các mạch khuếch đại, điện trở giúp ổn định tín hiệu đầu ra, đảm bảo hoạt động chính xác của thiết bị.
- Cảm biến nhiệt độ: Một số cảm biến nhiệt độ hoạt động dựa trên nguyên lý thay đổi điện trở theo nhiệt độ, ví dụ như cặp nhiệt điện hoặc điện trở nhiệt. Điều này cho phép đo nhiệt độ trong các ứng dụng công nghiệp và gia dụng.
- Mạch lọc tín hiệu: Trong các mạch điện, điện trở được kết hợp với tụ điện và cuộn cảm để tạo ra các bộ lọc tín hiệu, giúp loại bỏ các tần số nhiễu không mong muốn.
- Thiết bị sưởi: Điện trở cũng được sử dụng trong các thiết bị sưởi như lò sưởi, ấm đun nước, và bếp điện. Khi dòng điện chạy qua điện trở, năng lượng điện chuyển hóa thành nhiệt năng, giúp tạo ra nhiệt để làm nóng môi trường xung quanh.
- Khảo sát địa chất: Điện trở suất của đất được đo để khảo sát cấu trúc địa chất dưới lòng đất, hỗ trợ trong việc tìm kiếm tài nguyên như dầu mỏ và khoáng sản.
Những ứng dụng này cho thấy điện trở không chỉ là một khái niệm lý thuyết mà còn đóng vai trò quan trọng trong việc thiết kế và vận hành các thiết bị, công trình trong đời sống hàng ngày.

4. Các Yếu Tố Ảnh Hưởng Đến Điện Trở
Điện trở của một dây dẫn phụ thuộc vào nhiều yếu tố khác nhau. Hiểu rõ các yếu tố này sẽ giúp chúng ta có thể kiểm soát và thiết kế các mạch điện hiệu quả hơn. Dưới đây là các yếu tố chính ảnh hưởng đến điện trở:
- Chất liệu của dây dẫn: Mỗi chất liệu có điện trở suất \(\rho\) khác nhau. Chất liệu có điện trở suất thấp, như đồng hoặc nhôm, sẽ có điện trở nhỏ hơn so với các chất liệu như sắt hoặc niken.
- Chiều dài dây dẫn: Điện trở của một dây dẫn tỉ lệ thuận với chiều dài của nó. Cụ thể, khi chiều dài dây dẫn \(l\) tăng lên, điện trở \(R\) cũng tăng theo. Công thức tính điện trở dựa trên chiều dài là: \[ R = \frac{\rho \cdot l}{S} \]
- Tiết diện của dây dẫn: Điện trở tỉ lệ nghịch với diện tích tiết diện ngang của dây dẫn. Tiết diện \(S\) càng lớn, điện trở càng nhỏ. Đây là lý do tại sao các dây dẫn có tiết diện lớn thường được sử dụng để truyền tải điện năng với tổn thất ít hơn.
- Nhiệt độ: Nhiệt độ cũng có ảnh hưởng lớn đến điện trở. Với hầu hết các kim loại, khi nhiệt độ tăng, điện trở cũng tăng. Điều này là do sự gia tăng chuyển động nhiệt của các electron, làm tăng va chạm và cản trở dòng điện. Trong một số vật liệu đặc biệt như chất bán dẫn, nhiệt độ tăng có thể làm giảm điện trở.
- Tần số của dòng điện: Ở các tần số cao, hiệu ứng bề mặt có thể làm tăng điện trở hiệu dụng của dây dẫn. Đây là hiện tượng "hiệu ứng da", khi dòng điện tập trung chủ yếu ở bề mặt dây dẫn, làm giảm diện tích hiệu dụng của dòng điện và tăng điện trở.
Việc nắm bắt các yếu tố này sẽ giúp bạn thiết kế các hệ thống điện với hiệu suất tối ưu, đồng thời đảm bảo an toàn và tiết kiệm năng lượng trong quá trình sử dụng.

5. Phương Pháp Đo Và Tính Toán Điện Trở
Để đo và tính toán điện trở của một dây dẫn hay linh kiện điện tử, ta có thể áp dụng nhiều phương pháp khác nhau, từ các thiết bị đơn giản đến phức tạp. Dưới đây là các phương pháp phổ biến:
Sử Dụng Đồng Hồ Vạn Năng
- Chuẩn bị: Đặt đồng hồ vạn năng ở chế độ đo điện trở (ký hiệu Ω).
- Kết nối: Nối hai que đo của đồng hồ vạn năng vào hai đầu của vật cần đo điện trở.
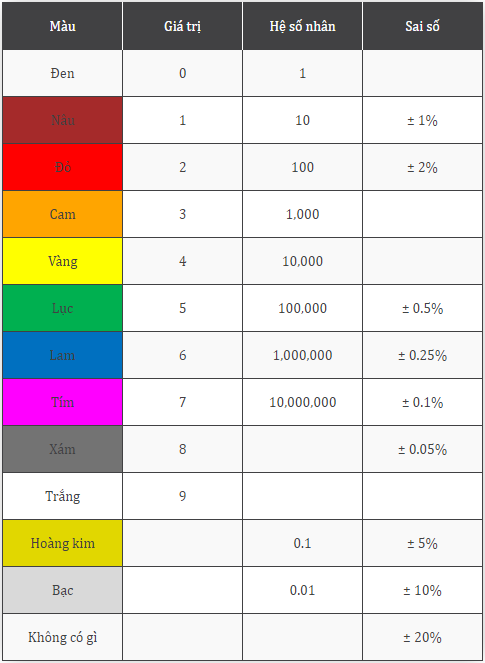
- Đọc kết quả: Đồng hồ sẽ hiển thị giá trị điện trở trên màn hình. Giá trị này có thể cần phải nhân với hệ số nếu đồng hồ có thang đo tự động.
Phương Pháp Suy Luận Qua Công Thức Ohm
Phương pháp này dựa trên công thức Ohm, \[R = \frac{U}{I}\], trong đó \(U\) là hiệu điện thế (V) và \(I\) là cường độ dòng điện (A).
- Đo hiệu điện thế: Sử dụng vôn kế để đo hiệu điện thế \(U\) giữa hai đầu của vật dẫn.
- Đo cường độ dòng điện: Dùng ampe kế để đo cường độ dòng điện \(I\) chạy qua vật dẫn.
- Tính toán điện trở: Áp dụng công thức trên để tính \(R\).
Sử Dụng Cầu Wheatstone
Cầu Wheatstone là một mạch đo điện trở chính xác, đặc biệt hữu ích trong các thí nghiệm vật lý.
- Cấu hình mạch: Kết nối vật cần đo điện trở vào một nhánh của cầu Wheatstone. Các nhánh khác sẽ chứa các điện trở chuẩn đã biết.
- Điều chỉnh: Điều chỉnh các điện trở biến trở trong mạch cho đến khi điện kế trong cầu chỉ số không (dòng điện qua điện kế bằng 0).
- Tính toán: Sử dụng công thức của cầu Wheatstone để tính điện trở chưa biết dựa trên các điện trở đã biết.
Việc lựa chọn phương pháp đo phù hợp tùy thuộc vào độ chính xác yêu cầu và thiết bị có sẵn. Nắm vững các phương pháp đo sẽ giúp bạn thực hiện các phép đo và tính toán điện trở một cách chính xác và hiệu quả.
XEM THÊM:
6. Bài Tập Thực Hành Và Ứng Dụng
Để củng cố kiến thức về điện trở và cách tính toán điện trở trong mạch điện, dưới đây là một số bài tập thực hành và ứng dụng thực tế mà các bạn học sinh lớp 9 có thể làm để nâng cao kỹ năng:
Bài Tập 1: Tính Điện Trở Dây Dẫn
- Cho một dây dẫn bằng nhôm có chiều dài \(l = 50 \, m\) và tiết diện ngang \(S = 2 \, mm^2\). Biết điện trở suất của nhôm là \(\rho = 2.82 \times 10^{-8} \, \Omega \cdot m\). Hãy tính điện trở của dây dẫn này.
- Giải: Áp dụng công thức: \[ R = \frac{\rho \cdot l}{S} \] Thay số: \[ R = \frac{2.82 \times 10^{-8} \times 50}{2 \times 10^{-6}} = 0.705 \, \Omega \]
Bài Tập 2: Xác Định Điện Trở Trong Mạch Nối Tiếp
- Có hai điện trở \(R_1 = 5 \, \Omega\) và \(R_2 = 10 \, \Omega\) được nối tiếp với nhau. Tính điện trở tổng của mạch.
- Giải: Điện trở tổng của mạch nối tiếp được tính bằng: \[ R_{tổng} = R_1 + R_2 = 5 \, \Omega + 10 \, \Omega = 15 \, \Omega \]
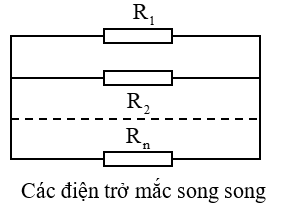
Bài Tập 3: Xác Định Điện Trở Trong Mạch Song Song
- Có hai điện trở \(R_1 = 6 \, \Omega\) và \(R_2 = 12 \, \Omega\) được nối song song với nhau. Tính điện trở tổng của mạch.
- Giải: Điện trở tổng của mạch song song được tính bằng: \[ \frac{1}{R_{tổng}} = \frac{1}{R_1} + \frac{1}{R_2} = \frac{1}{6 \, \Omega} + \frac{1}{12 \, \Omega} = \frac{1}{4 \, \Omega} \] \[ R_{tổng} = 4 \, \Omega \]
Ứng Dụng Thực Tế
- Thiết kế mạch điện: Kiến thức về điện trở giúp bạn thiết kế mạch điện trong các thiết bị điện tử, đảm bảo chúng hoạt động ổn định và an toàn.
- Chọn vật liệu dây dẫn: Dựa trên các bài tập tính điện trở, bạn có thể lựa chọn dây dẫn phù hợp cho các công trình điện trong gia đình hoặc công nghiệp, giảm thiểu tổn thất điện năng.
- Kiểm tra và sửa chữa thiết bị: Hiểu biết về điện trở giúp bạn xác định lỗi trong mạch điện, thay thế linh kiện hư hỏng và sửa chữa thiết bị điện.
Việc luyện tập thường xuyên với các bài tập và ứng dụng thực tế sẽ giúp bạn nắm vững kiến thức và áp dụng hiệu quả trong cuộc sống.





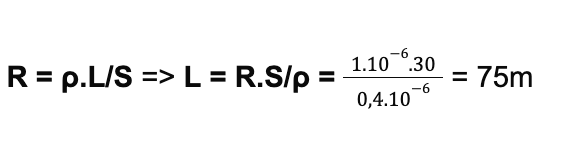





.png)




