Chủ đề công thức tính điện trở tương đương mắc nối tiếp: Công thức tính điện trở tương đương mắc nối tiếp là một khái niệm quan trọng trong vật lý và điện tử, giúp xác định tổng điện trở của một mạch nối tiếp. Bài viết này cung cấp hướng dẫn chi tiết, từ định nghĩa cơ bản đến các ví dụ minh họa và ứng dụng thực tế. Cùng tìm hiểu để nắm rõ công thức và áp dụng hiệu quả trong học tập cũng như thực tiễn.
Mục lục
Công Thức Tính Điện Trở Mắc Nối Tiếp
Trong vật lý và kỹ thuật điện, khi các điện trở được mắc nối tiếp với nhau trong một mạch điện, tổng điện trở của mạch sẽ là tổng các điện trở thành phần. Đây là một nguyên tắc cơ bản trong lý thuyết mạch điện.
Công thức tính điện trở mắc nối tiếp
Giả sử chúng ta có n điện trở \(R_1, R_2, R_3, \ldots, R_n\) được mắc nối tiếp với nhau. Tổng điện trở tương đương \(R_{tổng}\) của mạch được tính theo công thức:
\[
R_{tổng} = R_1 + R_2 + R_3 + \ldots + R_n
\]
Trong đó:
- \(R_{tổng}\): Tổng điện trở của mạch điện.
- \(R_1, R_2, R_3, \ldots, R_n\): Các điện trở thành phần trong mạch.
Ví dụ minh họa
Giả sử có ba điện trở với các giá trị lần lượt là \(R_1 = 5 \, \Omega\), \(R_2 = 10 \, \Omega\) và \(R_3 = 15 \, \Omega\) mắc nối tiếp trong một mạch. Khi đó, tổng điện trở của mạch là:
\[
R_{tổng} = 5 \, \Omega + 10 \, \Omega + 15 \, \Omega = 30 \, \Omega
\]
Đặc điểm của mạch điện mắc nối tiếp
- Dòng điện qua tất cả các điện trở là như nhau vì chỉ có một con đường cho dòng điện đi qua.
- Điện áp tổng cộng của mạch bằng tổng điện áp rơi trên từng điện trở.
- Nếu một điện trở trong mạch bị hỏng (ngắt mạch), dòng điện sẽ không thể tiếp tục chạy qua mạch.
Mạch điện mắc nối tiếp thường được sử dụng trong các ứng dụng cần sự đơn giản và dễ thiết kế, nhưng có nhược điểm là toàn bộ mạch sẽ bị ảnh hưởng nếu có một phần nào đó bị hỏng.

.png)
1. Định nghĩa về điện trở mắc nối tiếp
Điện trở mắc nối tiếp là cách kết nối các điện trở trong mạch điện sao cho dòng điện phải đi qua lần lượt từng điện trở một, không có bất kỳ nhánh rẽ nào. Trong mạch này, chỉ có một đường duy nhất cho dòng điện chạy qua, dẫn đến cường độ dòng điện tại mọi điểm trong mạch là như nhau.
Đặc điểm của mạch điện nối tiếp:
- Hiệu điện thế toàn mạch là tổng hiệu điện thế trên các điện trở thành phần.
- Cường độ dòng điện trong toàn mạch bằng cường độ dòng điện qua mỗi điện trở.
Công thức cơ bản để tính điện trở tương đương trong mạch nối tiếp là:
\[ R_{\text{tương đương}} = R_1 + R_2 + \ldots + R_n \]
Trong đó:
- \( R_1, R_2, \ldots, R_n \): là các giá trị điện trở thành phần trong mạch.
- \( R_{\text{tương đương}} \): là điện trở tổng cộng của mạch.
Điện trở tương đương trong mạch nối tiếp luôn lớn hơn hoặc bằng giá trị của từng điện trở thành phần riêng lẻ, và mỗi khi thêm một điện trở vào mạch, tổng điện trở sẽ tăng lên.
2. Công thức tính điện trở tương đương
Trong mạch điện mắc nối tiếp, điện trở tương đương được tính bằng cách cộng tổng các giá trị điện trở của từng thành phần trong mạch. Công thức chung như sau:
\[ R_{\text{tương đương}} = R_1 + R_2 + \ldots + R_n \]
Trong đó:
- \( R_1, R_2, \ldots, R_n \): là các điện trở thành phần trong mạch nối tiếp.
Đặc điểm quan trọng của mạch nối tiếp là:
- Cường độ dòng điện \( I \) tại mọi điểm trong mạch là như nhau.
- Hiệu điện thế tổng \( U \) của mạch là tổng hiệu điện thế trên mỗi điện trở: \[ U = U_1 + U_2 + \ldots + U_n \].
Điện trở tương đương trong mạch nối tiếp sẽ luôn lớn hơn hoặc bằng bất kỳ giá trị điện trở nào trong mạch. Việc tính toán chính xác điện trở tương đương giúp xác định đặc tính mạch, tối ưu hóa thiết kế và đảm bảo an toàn khi sử dụng các thiết bị điện.

3. Phân tích các ví dụ thực tiễn
Việc tính toán điện trở tương đương trong mạch nối tiếp không chỉ là lý thuyết mà còn rất hữu ích trong thực tiễn. Hãy xem xét các ví dụ dưới đây để hiểu rõ hơn cách áp dụng công thức vào thực tế.
Ví dụ 1: Mạch điện với ba điện trở nối tiếp
Giả sử có ba điện trở với giá trị lần lượt là \( R_1 = 2 \Omega \), \( R_2 = 3 \Omega \), và \( R_3 = 5 \Omega \) được mắc nối tiếp với nhau. Điện trở tương đương của mạch sẽ được tính như sau:
\[ R_{\text{tương đương}} = R_1 + R_2 + R_3 = 2 \Omega + 3 \Omega + 5 \Omega = 10 \Omega \]
Điều này cho thấy tổng điện trở tương đương lớn hơn bất kỳ điện trở thành phần nào trong mạch.
Ví dụ 2: Mạch nối tiếp với nhiều điện trở khác nhau
Xét một mạch điện có bốn điện trở: \( R_1 = 1 \Omega \), \( R_2 = 4 \Omega \), \( R_3 = 6 \Omega \), và \( R_4 = 9 \Omega \) được mắc nối tiếp. Ta có:
\[ R_{\text{tương đương}} = R_1 + R_2 + R_3 + R_4 = 1 \Omega + 4 \Omega + 6 \Omega + 9 \Omega = 20 \Omega \]
Với kết quả này, ta có thể dễ dàng xác định tổng điện trở của mạch và từ đó tính toán được các giá trị khác như cường độ dòng điện hoặc hiệu điện thế.
Nhận xét chung
Các ví dụ trên minh họa rằng khi các điện trở được mắc nối tiếp, giá trị điện trở tương đương luôn tăng lên, điều này ảnh hưởng trực tiếp đến hiệu suất của mạch điện. Để đảm bảo mạch hoạt động đúng yêu cầu, việc nắm vững cách tính điện trở tương đương là vô cùng quan trọng trong thiết kế và phân tích mạch điện.
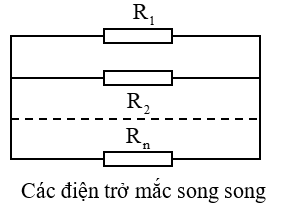
4. Ứng dụng thực tiễn của công thức điện trở tương đương
Công thức tính điện trở tương đương trong mạch nối tiếp không chỉ quan trọng trong lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Dưới đây là một số ví dụ điển hình:
4.1. Thiết kế mạch điện gia đình
Trong hệ thống điện gia đình, các thiết bị như đèn, công tắc thường được mắc nối tiếp để điều khiển dòng điện. Bằng cách hiểu rõ công thức tính điện trở tương đương, kỹ sư có thể đảm bảo an toàn và hiệu quả cho hệ thống điện trong nhà.
4.2. Tối ưu hóa hiệu suất của mạch điện
Trong các mạch điện công nghiệp hoặc mạch điện tử, việc tính toán điện trở tương đương giúp tối ưu hóa hiệu suất, giảm tiêu hao năng lượng và tránh quá tải. Điều này đặc biệt quan trọng trong việc thiết kế các mạch điện phức tạp.
4.3. Ứng dụng trong giáo dục và nghiên cứu
Công thức này là một phần không thể thiếu trong chương trình giảng dạy về điện và điện tử. Sinh viên và học sinh áp dụng công thức để giải các bài tập và thực hành, từ đó hiểu sâu hơn về đặc tính của mạch điện.
4.4. Bảo trì và sửa chữa thiết bị điện
Trong quá trình bảo trì và sửa chữa thiết bị điện, việc kiểm tra và thay thế các điện trở cần dựa trên việc tính toán điện trở tương đương. Điều này đảm bảo rằng thiết bị hoạt động ổn định và an toàn.
Từ các ví dụ trên, có thể thấy rằng việc nắm vững công thức tính điện trở tương đương không chỉ hỗ trợ trong việc học tập mà còn mang lại giá trị thiết thực trong công việc và cuộc sống.

5. Một số bài tập mẫu và hướng dẫn giải chi tiết
Để hiểu rõ hơn cách tính điện trở tương đương trong mạch nối tiếp, hãy cùng xem qua một số bài tập mẫu và các bước hướng dẫn chi tiết để giải quyết vấn đề.
Bài tập 1: Tính điện trở tương đương của mạch gồm 3 điện trở
Cho ba điện trở có giá trị lần lượt là \( R_1 = 5 \Omega \), \( R_2 = 10 \Omega \), và \( R_3 = 15 \Omega \) được mắc nối tiếp. Hãy tính điện trở tương đương của mạch.
Giải:
Điện trở tương đương của mạch được tính theo công thức:
\[ R_{\text{tương đương}} = R_1 + R_2 + R_3 \]
Thay các giá trị vào, ta có:
\[ R_{\text{tương đương}} = 5 \Omega + 10 \Omega + 15 \Omega = 30 \Omega \]
Vậy điện trở tương đương của mạch là \( 30 \Omega \).
Bài tập 2: Mạch nối tiếp với 4 điện trở khác nhau
Cho một mạch gồm 4 điện trở: \( R_1 = 2 \Omega \), \( R_2 = 3 \Omega \), \( R_3 = 7 \Omega \), và \( R_4 = 8 \Omega \). Hãy tính điện trở tương đương của mạch.
Giải:
Áp dụng công thức tính điện trở tương đương:
\[ R_{\text{tương đương}} = R_1 + R_2 + R_3 + R_4 \]
Thay các giá trị vào, ta có:
\[ R_{\text{tương đương}} = 2 \Omega + 3 \Omega + 7 \Omega + 8 \Omega = 20 \Omega \]
Vậy điện trở tương đương của mạch là \( 20 \Omega \).
Nhận xét:
Các bài tập trên cho thấy quy trình tính điện trở tương đương trong mạch nối tiếp khá đơn giản. Bạn chỉ cần cộng tổng các điện trở lại với nhau. Hãy áp dụng công thức này vào nhiều tình huống khác nhau để củng cố kiến thức.
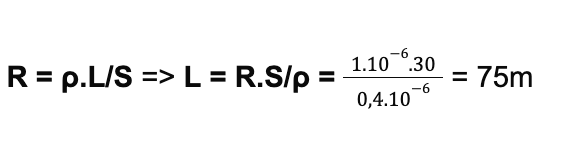



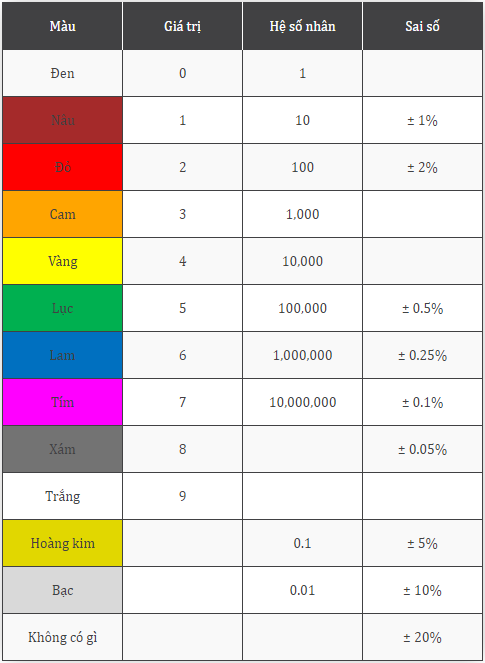



.png)




