Chủ đề công thức tính điện trở mạch ngoài: Bài viết này cung cấp một hướng dẫn toàn diện về công thức tính điện trở mạch ngoài, bao gồm các công thức cơ bản, ví dụ minh họa chi tiết, và các ứng dụng thực tế. Đây là tài liệu hữu ích cho học sinh, sinh viên, và những ai đang nghiên cứu về điện tử, giúp nắm vững kiến thức và áp dụng hiệu quả trong các bài tập và công việc thực tế.
Mục lục
- Công Thức Tính Điện Trở Mạch Ngoài
- 1. Giới Thiệu Chung Về Điện Trở Mạch Ngoài
- 2. Công Thức Tính Điện Trở Mạch Ngoài
- 3. Điện Trở Mạch Ngoài Trong Các Mạch Điện Cụ Thể
- 4. Lỗi Thường Gặp Và Lưu Ý Khi Tính Điện Trở Mạch Ngoài
- 5. Các Bài Tập Thực Hành Và Giải Bài Tập Về Điện Trở Mạch Ngoài
- 6. Các Công Thức Liên Quan Khác
Công Thức Tính Điện Trở Mạch Ngoài
Điện trở mạch ngoài là một phần quan trọng trong việc tính toán và thiết kế các mạch điện. Dưới đây là tổng hợp các công thức và hướng dẫn liên quan đến cách tính điện trở mạch ngoài, giúp bạn dễ dàng áp dụng vào thực tế.
1. Công Thức Tính Điện Trở Mạch Ngoài
Để tính điện trở mạch ngoài, công thức tổng quát được sử dụng là:
\[
R = \frac{E_b}{I} - r_b
\]
Trong đó:
- \(R\): Điện trở mạch ngoài (Ω)
- \(E_b\): Suất điện động của nguồn điện (V)
- \(I\): Cường độ dòng điện qua mạch (A)
- \(r_b\): Điện trở trong của nguồn điện (Ω)
2. Cách Tính Điện Trở Tương Đương
Công thức tính điện trở tương đương phụ thuộc vào cách mắc các điện trở trong mạch. Có hai dạng mắc điện trở phổ biến là mắc nối tiếp và mắc song song.
Mắc Nối Tiếp
Khi các điện trở được mắc nối tiếp, điện trở tương đương của toàn mạch được tính bằng tổng các điện trở thành phần:
\[
R_{tđ} = R_1 + R_2 + R_3 + \dots
\]
Mắc Song Song
Trong trường hợp các điện trở được mắc song song, điện trở tương đương của toàn mạch được tính bằng công thức:
\[
\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots
\]
3. Ứng Dụng Thực Tiễn
Việc tính toán điện trở mạch ngoài có ứng dụng rộng rãi trong các lĩnh vực như:
- Thiết kế hệ thống phân phối điện: Giúp tối ưu hóa dòng điện, giảm tổn thất năng lượng và đảm bảo an toàn.
- Công nghệ ô tô: Dùng trong thiết kế và kiểm tra các mạch điện, giúp tăng hiệu suất và độ bền của các bộ phận điện tử.
- Viễn thông: Hỗ trợ thiết kế và bảo trì các hệ thống truyền dẫn tín hiệu, đảm bảo chất lượng dịch vụ.
- Nghiên cứu và phát triển: Phát triển các thiết bị và công nghệ mới từ cảm biến đến các thiết bị điện tử tiên tiến.
4. Các Lỗi Thường Gặp Khi Tính Điện Trở Mạch Ngoài
Trong quá trình tính toán điện trở mạch ngoài, có một số lỗi phổ biến mà bạn cần lưu ý:
- Lỗi đo lường sai: Đảm bảo sử dụng thiết bị đo chính xác và điều chỉnh đúng cách.
- Lỗi tính toán: Kiểm tra lại các công thức và đơn vị để đảm bảo tính toán đúng.
- Bỏ qua điện trở trong: Đừng quên tính đến điện trở trong của nguồn điện trong các phép tính.
Việc nắm vững các công thức và nguyên tắc trên sẽ giúp bạn thực hiện các tính toán điện trở mạch ngoài một cách chính xác và hiệu quả hơn.

.png)
1. Giới Thiệu Chung Về Điện Trở Mạch Ngoài
Điện trở mạch ngoài là một khái niệm quan trọng trong lĩnh vực điện tử và vật lý, liên quan đến việc tính toán và phân tích các mạch điện. Điện trở mạch ngoài đề cập đến tổng trở của các thành phần trong mạch điện bên ngoài nguồn điện. Việc hiểu rõ điện trở mạch ngoài giúp bạn xác định đúng cường độ dòng điện và điện áp trong mạch, từ đó đảm bảo hiệu suất hoạt động và an toàn cho các thiết bị điện.
Trong các mạch điện, điện trở mạch ngoài thường bao gồm các điện trở nối tiếp và song song, mỗi loại sẽ có cách tính điện trở tương đương khác nhau. Tổng điện trở của mạch ngoài ảnh hưởng trực tiếp đến dòng điện chạy qua mạch, vì vậy, việc nắm bắt cách tính toán và ứng dụng công thức đúng đắn là rất cần thiết.
Để tính điện trở mạch ngoài, chúng ta sử dụng công thức tổng quát:
\[
R = \frac{E_b}{I} - r_b
\]
Trong đó:
- \(R\): Điện trở mạch ngoài (Ω)
- \(E_b\): Suất điện động của nguồn điện (V)
- \(I\): Cường độ dòng điện qua mạch (A)
- \(r_b\): Điện trở trong của nguồn điện (Ω)
Việc tính toán điện trở mạch ngoài không chỉ giúp bạn hiểu rõ hơn về nguyên lý hoạt động của mạch điện mà còn đóng vai trò quan trọng trong thiết kế và kiểm tra các mạch điện tử, từ các thiết bị gia dụng đến các hệ thống công nghiệp phức tạp.
2. Công Thức Tính Điện Trở Mạch Ngoài
Công thức tính điện trở mạch ngoài là một phần quan trọng trong việc phân tích và thiết kế các mạch điện. Điện trở mạch ngoài không chỉ ảnh hưởng đến hiệu suất của mạch mà còn liên quan trực tiếp đến việc tính toán các thông số khác như dòng điện và điện áp. Dưới đây là các công thức và bước tính toán cụ thể để xác định điện trở mạch ngoài.
2.1. Công Thức Tổng Quát
Công thức tổng quát để tính điện trở mạch ngoài được biểu diễn như sau:
\[
R = \frac{E_b}{I} - r_b
\]
Trong đó:
- \(R\): Điện trở mạch ngoài (Ω)
- \(E_b\): Suất điện động của nguồn điện (V)
- \(I\): Cường độ dòng điện chạy qua mạch (A)
- \(r_b\): Điện trở trong của nguồn điện (Ω)
2.2. Công Thức Trong Các Trường Hợp Đặc Biệt
Trong một số trường hợp đặc biệt, công thức tính điện trở mạch ngoài có thể được điều chỉnh để phù hợp với cấu trúc của mạch. Ví dụ:
- Đối với mạch nối tiếp: Điện trở mạch ngoài là tổng của các điện trở thành phần trong mạch: \[ R_{tđ} = R_1 + R_2 + R_3 + \dots \]
- Đối với mạch song song: Điện trở mạch ngoài được tính bằng nghịch đảo của tổng các nghịch đảo của điện trở thành phần: \[ \frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots \]
2.3. Ví Dụ Minh Họa
Để làm rõ hơn các công thức trên, chúng ta cùng xem xét một ví dụ cụ thể:
Giả sử bạn có một mạch gồm một nguồn điện với suất điện động \(E_b = 12V\) và điện trở trong \(r_b = 1Ω\), mạch ngoài gồm một điện trở \(R = 4Ω\). Cường độ dòng điện qua mạch là \(I = 2A\). Khi đó, điện trở mạch ngoài được tính như sau:
\[
R = \frac{E_b}{I} - r_b = \frac{12V}{2A} - 1Ω = 6Ω - 1Ω = 5Ω
\]
Như vậy, điện trở mạch ngoài trong ví dụ này là \(5Ω\). Đây là cách đơn giản để tính toán và xác định điện trở mạch ngoài dựa trên các thông số của mạch điện.

3. Điện Trở Mạch Ngoài Trong Các Mạch Điện Cụ Thể
Điện trở mạch ngoài có vai trò quan trọng trong việc phân tích và thiết kế các mạch điện cụ thể. Dưới đây là cách tính toán và áp dụng điện trở mạch ngoài trong ba loại mạch điện phổ biến: mạch nối tiếp, mạch song song, và mạch hỗn hợp.
3.1. Điện Trở Mạch Ngoài Trong Mạch Nối Tiếp
Trong mạch nối tiếp, các điện trở được nối liên tiếp với nhau, dòng điện chạy qua mỗi điện trở là như nhau. Điện trở mạch ngoài trong mạch nối tiếp được tính bằng tổng các điện trở thành phần:
\[
R_{tđ} = R_1 + R_2 + R_3 + \dots + R_n
\]
Ví dụ, nếu bạn có ba điện trở \(R_1 = 2Ω\), \(R_2 = 3Ω\), và \(R_3 = 5Ω\) nối tiếp trong mạch, thì điện trở mạch ngoài sẽ là:
\[
R_{tđ} = 2Ω + 3Ω + 5Ω = 10Ω
\]
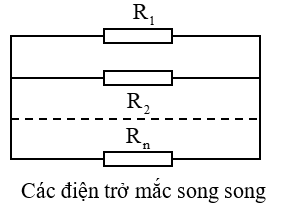
3.2. Điện Trở Mạch Ngoài Trong Mạch Song Song
Trong mạch song song, các điện trở được nối song song với nhau, dòng điện được chia đều qua các nhánh. Điện trở mạch ngoài trong mạch song song được tính bằng cách lấy nghịch đảo của tổng các nghịch đảo của các điện trở thành phần:
\[
\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}
\]
Ví dụ, với ba điện trở \(R_1 = 4Ω\), \(R_2 = 6Ω\), và \(R_3 = 12Ω\) mắc song song, điện trở mạch ngoài sẽ được tính như sau:
\[
\frac{1}{R_{tđ}} = \frac{1}{4Ω} + \frac{1}{6Ω} + \frac{1}{12Ω} = \frac{3 + 2 + 1}{12} = \frac{6}{12} = 0.5Ω
\]
Vậy điện trở mạch ngoài trong trường hợp này là:
\[
R_{tđ} = 2Ω
\]
3.3. Điện Trở Mạch Ngoài Trong Mạch Hỗn Hợp
Mạch hỗn hợp là sự kết hợp giữa mạch nối tiếp và mạch song song. Để tính điện trở mạch ngoài trong mạch hỗn hợp, trước tiên ta cần phân tích mạch thành các phần nối tiếp và song song riêng biệt, sau đó tính điện trở cho từng phần và kết hợp lại.
Ví dụ, giả sử có một mạch gồm hai điện trở \(R_1 = 2Ω\) và \(R_2 = 3Ω\) nối tiếp với nhau, đồng thời mạch này được nối song song với một điện trở \(R_3 = 6Ω\). Đầu tiên, tính điện trở của phần nối tiếp:
\[
R_{12} = R_1 + R_2 = 2Ω + 3Ω = 5Ω
\]
Sau đó, tính điện trở tổng của mạch ngoài:
\[
\frac{1}{R_{tđ}} = \frac{1}{R_{12}} + \frac{1}{R_3} = \frac{1}{5Ω} + \frac{1}{6Ω} = \frac{6 + 5}{30} = \frac{11}{30} ≈ 0.367Ω
\]
Cuối cùng, điện trở mạch ngoài là:
\[
R_{tđ} ≈ 2.73Ω
\]
Việc nắm rõ cách tính điện trở mạch ngoài trong các loại mạch điện khác nhau giúp bạn thiết kế và phân tích mạch hiệu quả, đảm bảo hoạt động ổn định và an toàn cho các thiết bị điện tử.

4. Lỗi Thường Gặp Và Lưu Ý Khi Tính Điện Trở Mạch Ngoài
Khi tính toán điện trở mạch ngoài, một số lỗi phổ biến có thể xảy ra, dẫn đến kết quả không chính xác và ảnh hưởng đến hiệu suất của mạch điện. Dưới đây là một số lỗi thường gặp và các lưu ý quan trọng để tránh sai sót.
4.1. Lỗi Thường Gặp
- Không tính đến điện trở trong của nguồn điện: Một sai lầm phổ biến là bỏ qua điện trở trong của nguồn điện khi tính toán điện trở mạch ngoài. Điều này có thể dẫn đến việc ước lượng sai dòng điện và điện áp trong mạch.
- Lỗi khi tính điện trở trong mạch hỗn hợp: Trong mạch hỗn hợp, việc phân tích sai các phần nối tiếp và song song có thể dẫn đến kết quả tính toán sai lầm. Đặc biệt, khi có nhiều nhánh trong mạch, cần cẩn thận trong việc xác định cấu trúc mạch.
- Nhầm lẫn đơn vị đo: Đôi khi, việc sử dụng sai đơn vị đo hoặc không nhất quán trong đơn vị (chẳng hạn như Ω, kΩ, MΩ) có thể gây ra những sai sót nghiêm trọng trong quá trình tính toán.
- Sử dụng sai công thức: Việc không nắm vững công thức hoặc áp dụng sai công thức cho từng loại mạch (nối tiếp, song song, hỗn hợp) là một lỗi thường gặp, làm cho kết quả tính toán không chính xác.
4.2. Lưu Ý Khi Tính Toán
- Kiểm tra kỹ cấu trúc mạch: Trước khi bắt đầu tính toán, hãy chắc chắn rằng bạn đã hiểu rõ cấu trúc của mạch điện, đặc biệt là sự sắp xếp của các điện trở (nối tiếp hoặc song song).
- Sử dụng đơn vị đúng: Luôn chú ý đến việc sử dụng đơn vị đúng cho điện trở, dòng điện và điện áp. Sử dụng sai đơn vị sẽ dẫn đến kết quả không chính xác.
- Xem xét tất cả các thành phần trong mạch: Đảm bảo rằng bạn đã xem xét tất cả các thành phần trong mạch, bao gồm cả điện trở trong của nguồn điện, để có được kết quả chính xác nhất.
- Sử dụng công thức phù hợp: Hãy đảm bảo rằng bạn đang sử dụng đúng công thức cho từng loại mạch điện cụ thể. Nếu có sự kết hợp giữa các mạch nối tiếp và song song, hãy phân tích từng phần trước khi tính toán điện trở tổng.
Nhận thức và tránh những lỗi phổ biến này sẽ giúp bạn thực hiện các phép tính điện trở mạch ngoài một cách chính xác và hiệu quả hơn, đảm bảo mạch điện hoạt động đúng với thiết kế và an toàn.

5. Các Bài Tập Thực Hành Và Giải Bài Tập Về Điện Trở Mạch Ngoài
Để nắm vững kiến thức về điện trở mạch ngoài, việc thực hành qua các bài tập là cần thiết. Dưới đây là một số bài tập thực hành kèm theo hướng dẫn giải chi tiết, giúp bạn củng cố và áp dụng kiến thức đã học.
5.1. Bài Tập 1: Tính Điện Trở Mạch Ngoài Trong Mạch Nối Tiếp
Cho một mạch điện gồm ba điện trở nối tiếp: \(R_1 = 2Ω\), \(R_2 = 4Ω\), và \(R_3 = 6Ω\). Hãy tính điện trở mạch ngoài.
- Giải: Trong mạch nối tiếp, điện trở mạch ngoài được tính bằng tổng các điện trở thành phần:
- \[ R_{tđ} = R_1 + R_2 + R_3 = 2Ω + 4Ω + 6Ω = 12Ω \]
5.2. Bài Tập 2: Tính Điện Trở Mạch Ngoài Trong Mạch Song Song
Một mạch điện gồm ba điện trở mắc song song: \(R_1 = 3Ω\), \(R_2 = 6Ω\), và \(R_3 = 9Ω\). Tính điện trở mạch ngoài.
- Giải: Trong mạch song song, điện trở mạch ngoài được tính bằng công thức:
- \[ \frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{3Ω} + \frac{1}{6Ω} + \frac{1}{9Ω} \]
- Tính toán:
- \[ \frac{1}{R_{tđ}} = \frac{6 + 3 + 2}{18} = \frac{11}{18} \]
- Do đó, \(R_{tđ} ≈ 1.64Ω\).
5.3. Bài Tập 3: Mạch Hỗn Hợp
Một mạch gồm \(R_1 = 5Ω\) và \(R_2 = 10Ω\) nối tiếp với nhau, cả hai sau đó mắc song song với \(R_3 = 15Ω\). Tính điện trở mạch ngoài.
- Giải: Trước tiên, tính điện trở của phần nối tiếp:
- \[ R_{12} = R_1 + R_2 = 5Ω + 10Ω = 15Ω \]
- Sau đó, tính điện trở tổng của mạch ngoài:
- \[ \frac{1}{R_{tđ}} = \frac{1}{R_{12}} + \frac{1}{R_3} = \frac{1}{15Ω} + \frac{1}{15Ω} = \frac{2}{15} \]
- Vậy điện trở mạch ngoài là:
- \[ R_{tđ} = 7.5Ω \]
5.4. Bài Tập 4: Phân Tích Sai Lầm Trong Tính Toán
Giả sử có một mạch với \(R_1 = 4Ω\) mắc nối tiếp với một nhánh song song gồm \(R_2 = 8Ω\) và \(R_3 = 12Ω\). Một học sinh tính điện trở mạch ngoài là \(R_{tđ} = 14Ω\). Hãy phân tích lỗi sai.
- Giải: Lỗi sai ở đây là học sinh đã không phân tích đúng cấu trúc mạch. Đầu tiên, cần tính điện trở của nhánh song song:
- \[ \frac{1}{R_{23}} = \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{8Ω} + \frac{1}{12Ω} = \frac{5}{24} \]
- Vậy:
- \[ R_{23} ≈ 4.8Ω \]
- Sau đó:
- \[ R_{tđ} = R_1 + R_{23} ≈ 4Ω + 4.8Ω = 8.8Ω \]
- Do đó, kết quả đúng là \(R_{tđ} ≈ 8.8Ω\), không phải 14Ω.
Thông qua việc giải các bài tập này, bạn có thể nắm vững các phương pháp tính toán điện trở mạch ngoài và tránh được những lỗi phổ biến.
XEM THÊM:
6. Các Công Thức Liên Quan Khác
6.1. Công Thức Tính Điện Trở Tương Đương
Trong mạch điện, điện trở tương đương giúp chúng ta tính toán dễ dàng hơn khi có nhiều điện trở mắc nối tiếp hoặc song song. Công thức tính điện trở tương đương phụ thuộc vào cách mắc điện trở:
- Mạch nối tiếp:
- Mạch song song:
Trong mạch nối tiếp, điện trở tương đương \( R_{tđ} \) bằng tổng các điện trở thành phần:
\[
R_{tđ} = R_1 + R_2 + \dots + R_n
\]
Trong mạch song song, nghịch đảo của điện trở tương đương bằng tổng nghịch đảo của các điện trở thành phần:
\[
\frac{1}{R_{tđ}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}
\]
6.2. Công Thức Tính Điện Trở Theo Vật Liệu Và Kích Thước
Điện trở của một dây dẫn phụ thuộc vào điện trở suất của vật liệu, chiều dài và tiết diện của dây dẫn. Công thức cụ thể như sau:
\[
R = \rho \frac{L}{S}
\]
- \( R \): Điện trở của dây dẫn (Ohm).
- \( \rho \): Điện trở suất của vật liệu (Ohm.m).
- \( L \): Chiều dài của dây dẫn (m).
- \( S \): Tiết diện của dây dẫn (m²).
Điện trở suất \( \rho \) phụ thuộc vào loại vật liệu và nhiệt độ. Khi nhiệt độ tăng, điện trở suất của hầu hết các vật liệu sẽ tăng lên, dẫn đến điện trở cũng tăng theo.
6.3. Các Công Thức Liên Quan Khác Trong Mạch Điện
Ngoài công thức tính điện trở, còn có một số công thức liên quan quan trọng trong mạch điện:
- Công Thức Định Luật Ohm:
- Công Thức Công Suất Điện:
- Công Thức Điện Dung Và Điện Trở:
- \( \tau \): Hằng số thời gian (giây).
- \( R \): Điện trở (Ohm).
- \( C \): Điện dung của tụ điện (Farad).
Định luật Ohm mô tả mối quan hệ giữa điện áp \( V \), dòng điện \( I \) và điện trở \( R \):
\[
V = I \cdot R
\]
Công suất tiêu thụ trong một đoạn mạch có thể tính bằng:
\[
P = V \cdot I = I^2 \cdot R = \frac{V^2}{R}
\]
Trong các mạch RC (mạch có điện trở và tụ điện), thời gian nạp và xả của tụ điện có thể được xác định bởi hằng số thời gian \( \tau \), với:
\[
\tau = R \cdot C
\]
Trong đó:




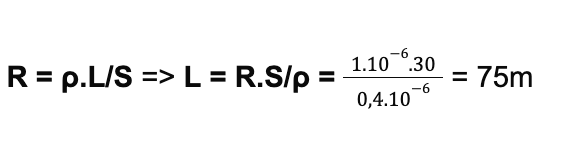





.png)




