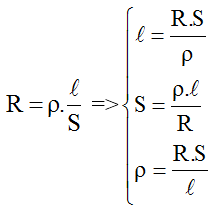Các Công Thức Tính Điện Trở Lớp 9: Hướng Dẫn Chi Tiết và Bài Tập Ứng Dụng

Trong chương trình Vật lý lớp 9, học sinh được học về các công thức tính điện trở của dây dẫn và các công thức liên quan. Dưới đây là tổng hợp các công thức và khái niệm quan trọng trong chủ đề này.

I. Công Thức Tính Điện Trở Của Dây Dẫn

Điện trở của một dây dẫn được tính dựa trên chiều dài, tiết diện và vật liệu của dây dẫn theo công thức:

\[
R = \rho \cdot \frac{l}{S}
\]

• \(R\): Điện trở (\(\Omega\))
• \(\rho\): Điện trở suất của vật liệu làm dây dẫn (\(\Omega \cdot m\))
• \(l\): Chiều dài của dây dẫn (m)
• \(S\): Tiết diện ngang của dây dẫn (m²)

II. Định Luật Ôm

Định luật Ôm là cơ sở để tính toán các đại lượng điện trong mạch điện. Công thức của định luật Ôm cho đoạn mạch có dạng:

\[
I = \frac{U}{R}
\]

• \(I\): Cường độ dòng điện (A)
• \(U\): Hiệu điện thế (V)

III. Công Thức Tính Điện Trở Tương Đương

1. Mạch Nối Tiếp

Trong mạch nối tiếp, điện trở tương đương được tính bằng tổng các điện trở thành phần:

\[
R_{td} = R_1 + R_2 + \dots + R_n
\]

2. Mạch Song Song

Trong mạch song song, điện trở tương đương được tính theo công thức:

\[
\frac{1}{R_{td}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}
\]

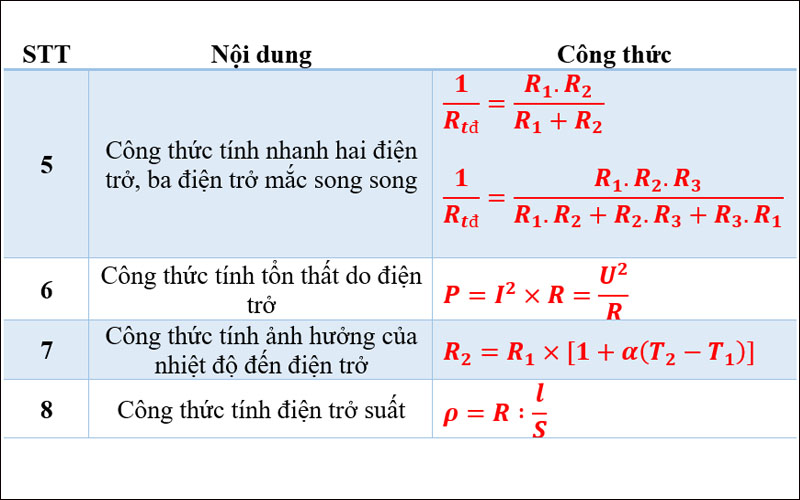
Hoặc với hai điện trở:

\[
R_{td} = \frac{R_1 \cdot R_2}{R_1 + R_2}
\]

IV. Một Số Lưu Ý Khi Giải Bài Tập

• Xác định rõ loại mạch (nối tiếp, song song hay hỗn hợp) để áp dụng đúng công thức.
• Kiểm tra đơn vị và chuyển đổi khi cần thiết.
• Sử dụng đúng công thức và tính toán cẩn thận để tránh sai sót.

Các công thức trên là những kiến thức cơ bản nhưng rất quan trọng giúp học sinh hiểu rõ hơn về nguyên lý hoạt động của mạch điện cũng như cách tính toán các đại lượng điện trong các bài tập thực tế.

Điện trở là một đại lượng vật lý quan trọng trong các mạch điện, đại diện cho khả năng cản trở dòng điện của vật liệu. Điện trở được ký hiệu bằng chữ \( R \) và đo bằng đơn vị Ohm (\(\Omega\)). Hiểu rõ khái niệm điện trở là nền tảng để giải các bài toán mạch điện, từ việc tính toán điện áp, dòng điện đến điện năng tiêu thụ.

Các yếu tố ảnh hưởng đến điện trở của một dây dẫn bao gồm:

• Chiều dài của dây dẫn (\(l\)): Điện trở tỉ lệ thuận với chiều dài dây dẫn. Dây càng dài, điện trở càng lớn.
• Tiết diện dây dẫn (\(S\)): Điện trở tỉ lệ nghịch với tiết diện. Dây có tiết diện càng lớn, điện trở càng nhỏ.
• Vật liệu làm dây dẫn (\(\rho\)): Mỗi vật liệu có điện trở suất khác nhau, đặc trưng cho khả năng dẫn điện của nó. Vật liệu có điện trở suất nhỏ dẫn điện tốt hơn.

Công thức tính điện trở của dây dẫn được biểu diễn như sau:

\[
R = \rho \cdot \frac{l}{S}
\]

Trong đó:

• \(R\) là điện trở (\(\Omega\)).
• \(\rho\) là điện trở suất của vật liệu (\(\Omega \cdot m\)).
• \(l\) là chiều dài dây dẫn (m).
• \(S\) là tiết diện dây dẫn (m²).

Điện trở có vai trò quan trọng trong việc điều chỉnh và kiểm soát dòng điện trong mạch. Các ứng dụng của điện trở rất đa dạng, từ bảo vệ mạch điện, điều chỉnh cường độ dòng điện đến sử dụng trong các thiết bị điện tử khác nhau.

Điện trở của dây dẫn là đại lượng vật lý biểu thị mức độ cản trở dòng điện của vật liệu làm dây dẫn. Công thức tính điện trở của dây dẫn phụ thuộc vào các yếu tố như chiều dài, tiết diện và vật liệu của dây dẫn.

Công thức tính điện trở của dây dẫn được xác định theo phương trình:

\[
R = \rho \cdot \frac{l}{S}
\]

Trong đó:

• \(\rho\) là điện trở suất của vật liệu (\(\Omega \cdot m\)). Điện trở suất là một hằng số đặc trưng cho mỗi loại vật liệu và cho biết khả năng cản trở dòng điện của vật liệu đó.
• \(l\) là chiều dài của dây dẫn (m). Điện trở tỉ lệ thuận với chiều dài của dây dẫn, nghĩa là khi chiều dài tăng thì điện trở cũng tăng.
• \(S\) là tiết diện ngang của dây dẫn (m²). Điện trở tỉ lệ nghịch với tiết diện dây dẫn, nghĩa là dây dẫn có tiết diện càng lớn thì điện trở càng nhỏ.

Ví dụ, với dây dẫn bằng đồng có chiều dài \(l = 2 \, m\) và tiết diện \(S = 0.5 \times 10^{-6} \, m^2\), với điện trở suất của đồng là \(\rho = 1.68 \times 10^{-8} \, \Omega \cdot m\), điện trở của dây dẫn sẽ được tính như sau:

\[
R = 1.68 \times 10^{-8} \cdot \frac{2}{0.5 \times 10^{-6}} = 6.72 \, \Omega
\]

Công thức này là cơ sở để tính toán điện trở của bất kỳ dây dẫn nào, từ đó xác định khả năng dẫn điện của vật liệu, cũng như ứng dụng trong thiết kế và phân tích các mạch điện.

Định luật Ôm là một trong những nguyên lý cơ bản của điện học, được phát biểu bởi nhà vật lý người Đức Georg Simon Ohm. Định luật này mô tả mối quan hệ giữa hiệu điện thế (\(U\)), cường độ dòng điện (\(I\)), và điện trở (\(R\)) trong một mạch điện.

Theo định luật Ôm, cường độ dòng điện chạy qua một dây dẫn tỉ lệ thuận với hiệu điện thế đặt vào hai đầu dây và tỉ lệ nghịch với điện trở của dây dẫn. Công thức của định luật Ôm được viết như sau:

\[
I = \frac{U}{R}
\]

Trong đó:

• \(I\) là cường độ dòng điện chạy qua dây dẫn (A).
• \(U\) là hiệu điện thế giữa hai đầu dây dẫn (V).
• \(R\) là điện trở của dây dẫn (\(\Omega\)).

Định luật Ôm có thể được diễn giải qua các bước sau:

1. Xác định các đại lượng cần tính toán: Trước hết, cần xác định các giá trị của hiệu điện thế, cường độ dòng điện, hoặc điện trở, tùy thuộc vào đề bài yêu cầu.
2. Áp dụng công thức: Sử dụng công thức \(I = \frac{U}{R}\) để tính toán cường độ dòng điện, hoặc biến đổi công thức để tính \(U = I \cdot R\) khi cần xác định hiệu điện thế, hoặc \(R = \frac{U}{I}\) để tìm điện trở.
3. Kiểm tra kết quả: Sau khi tính toán, cần kiểm tra đơn vị của các đại lượng để đảm bảo tính đúng đắn và chính xác của kết quả.

Định luật Ôm không chỉ được áp dụng trong các bài toán lý thuyết mà còn là cơ sở để phân tích và thiết kế các mạch điện trong thực tế, như mạch điện trong thiết bị điện tử, hệ thống điện dân dụng và công nghiệp.

Điện trở tương đương là một giá trị điện trở thay thế cho toàn bộ hệ thống mạch điện, giúp đơn giản hóa việc tính toán và phân tích mạch. Tùy vào cách bố trí của các điện trở trong mạch, chúng ta có hai trường hợp chính để tính điện trở tương đương: mạch nối tiếp và mạch song song.

1. Mạch Nối Tiếp

Trong mạch nối tiếp, các điện trở được mắc liên tiếp nhau, nghĩa là dòng điện phải đi qua từng điện trở một. Điện trở tương đương trong mạch nối tiếp được tính bằng tổng các điện trở:

\[
R_{td} = R_1 + R_2 + R_3 + \dots + R_n
\]

Trong đó:

• \(R_{td}\) là điện trở tương đương (\(\Omega\)).
• \(R_1, R_2, R_3, \dots, R_n\) là các điện trở thành phần trong mạch (\(\Omega\)).

Điện trở tương đương trong mạch nối tiếp luôn lớn hơn bất kỳ điện trở nào trong các thành phần, và nó ảnh hưởng trực tiếp đến cường độ dòng điện trong mạch.

2. Mạch Song Song

Trong mạch song song, các điện trở được mắc song song với nhau, nghĩa là dòng điện có thể phân chia và đi qua các nhánh khác nhau. Điện trở tương đương trong mạch song song được tính theo công thức:

\[
\frac{1}{R_{td}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}
\]

Hoặc:

\[
R_{td} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}}
\]

Trong đó:

• \(R_{td}\) là điện trở tương đương (\(\Omega\)).
• \(R_1, R_2, R_3, \dots, R_n\) là các điện trở thành phần trong mạch (\(\Omega\)).

Điện trở tương đương trong mạch song song luôn nhỏ hơn bất kỳ điện trở nào trong các thành phần, điều này cho phép dòng điện trong mạch song song lớn hơn so với mạch nối tiếp.

Bằng cách tính toán đúng điện trở tương đương, ta có thể dễ dàng phân tích các mạch điện phức tạp và dự đoán được cường độ dòng điện, hiệu điện thế trong mạch, từ đó đảm bảo hoạt động an toàn và hiệu quả của hệ thống điện.

Để nắm vững và áp dụng các công thức tính điện trở đã học, việc luyện tập qua các bài tập thực hành là rất cần thiết. Dưới đây là một số bài tập ứng dụng giúp bạn củng cố kiến thức về điện trở, định luật Ôm, và cách tính điện trở tương đương.

Bài Tập 1: Tính Điện Trở của Dây Dẫn

Một dây dẫn bằng sắt có chiều dài \( l = 5 \, m \) và tiết diện \( S = 0.2 \times 10^{-6} \, m^2 \). Điện trở suất của sắt là \( \rho = 10 \times 10^{-8} \, \Omega \cdot m \). Tính điện trở của dây dẫn.

Lời Giải:

Sử dụng công thức:

\[
R = \rho \cdot \frac{l}{S}
\]

Thay các giá trị vào công thức:

\[
R = 10 \times 10^{-8} \cdot \frac{5}{0.2 \times 10^{-6}} = 25 \, \Omega
\]

Bài Tập 2: Áp Dụng Định Luật Ôm

Cho một mạch điện có điện trở \( R = 10 \, \Omega \) và cường độ dòng điện chạy qua mạch là \( I = 2 \, A \). Tính hiệu điện thế giữa hai đầu điện trở.

Lời Giải:

Sử dụng định luật Ôm:

\[
U = I \cdot R
\]

Thay các giá trị vào công thức:

\[
U = 2 \cdot 10 = 20 \, V
\]

Bài Tập 3: Tính Điện Trở Tương Đương Trong Mạch Nối Tiếp

Một mạch điện nối tiếp gồm ba điện trở có giá trị lần lượt là \( R_1 = 5 \, \Omega \), \( R_2 = 10 \, \Omega \), và \( R_3 = 15 \, \Omega \). Tính điện trở tương đương của mạch.

Lời Giải:

Sử dụng công thức tính điện trở tương đương cho mạch nối tiếp:

\[
R_{td} = R_1 + R_2 + R_3
\]

Thay các giá trị vào công thức:

\[
R_{td} = 5 + 10 + 15 = 30 \, \Omega
\]

Bài Tập 4: Tính Điện Trở Tương Đương Trong Mạch Song Song

Một mạch điện song song gồm ba điện trở có giá trị lần lượt là \( R_1 = 6 \, \Omega \), \( R_2 = 12 \, \Omega \), và \( R_3 = 18 \, \Omega \). Tính điện trở tương đương của mạch.

Lời Giải:

Sử dụng công thức tính điện trở tương đương cho mạch song song:

\[
\frac{1}{R_{td}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\]

Thay các giá trị vào công thức:

\[
\frac{1}{R_{td}} = \frac{1}{6} + \frac{1}{12} + \frac{1}{18} = \frac{1}{3} \, \Omega^{-1}
\]

Suy ra:

\[
R_{td} = 3 \, \Omega
\]

Các bài tập này không chỉ giúp bạn ôn luyện kiến thức mà còn nâng cao kỹ năng giải quyết vấn đề trong các tình huống thực tế liên quan đến mạch điện.

Khi giải các bài tập về điện trở, học sinh cần chú ý một số điểm sau để đảm bảo tính chính xác và tránh sai sót trong quá trình tính toán:

1. Cách xác định loại mạch điện

Trước khi bắt đầu tính toán, cần xác định chính xác loại mạch điện là mạch nối tiếp, song song hay hỗn hợp. Đây là bước quan trọng vì mỗi loại mạch có cách tính điện trở tương đương khác nhau:

• Mạch nối tiếp: Tổng điện trở được tính bằng tổng các điện trở thành phần: \( R_{tổng} = R_1 + R_2 + \dots + R_n \).
• Mạch song song: Điện trở tương đương được tính bằng công thức: \( \frac{1}{R_{tổng}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n} \).
• Mạch hỗn hợp: Kết hợp các phương pháp tính trên để tính toán.

2. Kiểm tra đơn vị và chuyển đổi

Luôn đảm bảo rằng các đơn vị đo được sử dụng trong bài toán là thống nhất. Ví dụ, chiều dài dây dẫn có thể đo bằng mét (m), đường kính hoặc bán kính đo bằng milimét (mm), và điện trở đo bằng ôm (Ω). Nếu cần, hãy chuyển đổi đơn vị trước khi thực hiện các phép tính:

• \( 1 \, \text{m} = 1000 \, \text{mm} \)
• \( 1 \, \text{kΩ} = 1000 \, \text{Ω} \)

3. Kỹ thuật tính toán nhanh và chính xác

Áp dụng các mẹo và kỹ thuật sau để giúp tính toán nhanh hơn và chính xác hơn:

1. Rút gọn mạch điện: Trước khi tính toán, hãy rút gọn mạch điện bằng cách kết hợp các điện trở tương đương (nếu có) để đơn giản hóa.
2. Sử dụng máy tính cầm tay: Sử dụng máy tính để thực hiện các phép nhân, chia và căn bậc hai để tránh sai sót do tính toán thủ công.
3. Kiểm tra lại kết quả: Sau khi tính toán, nên kiểm tra lại các bước tính và đối chiếu với đơn vị của kết quả để đảm bảo tính đúng đắn.

Cuối cùng, hãy luôn ghi nhớ rằng việc giải các bài tập về điện trở không chỉ yêu cầu kiến thức lý thuyết mà còn cần sự tỉ mỉ trong từng bước tính toán. Với sự chuẩn bị kỹ lưỡng và chú ý đến từng chi tiết, bạn sẽ dễ dàng đạt được kết quả chính xác và hiệu quả nhất.