Chủ đề các công thức tính điện trở suất: Các công thức tính điện trở suất là kiến thức quan trọng trong vật lý, giúp hiểu rõ hơn về khả năng cản trở dòng điện của vật liệu. Bài viết này sẽ cung cấp hướng dẫn chi tiết từ các công thức cơ bản đến nâng cao, cùng với các ứng dụng thực tiễn, giúp bạn nắm vững và áp dụng hiệu quả trong học tập cũng như công việc.
Mục lục
Các Công Thức Tính Điện Trở Suất
Điện trở suất là một đại lượng vật lý quan trọng trong lĩnh vực điện học, được ký hiệu là \( \rho \) và có đơn vị là \( \Omega \cdot m \) (Ohm mét). Điện trở suất cho biết mức độ cản trở dòng điện của một vật liệu và phụ thuộc vào bản chất của vật liệu đó. Dưới đây là các công thức cơ bản và thông tin chi tiết liên quan đến điện trở suất.
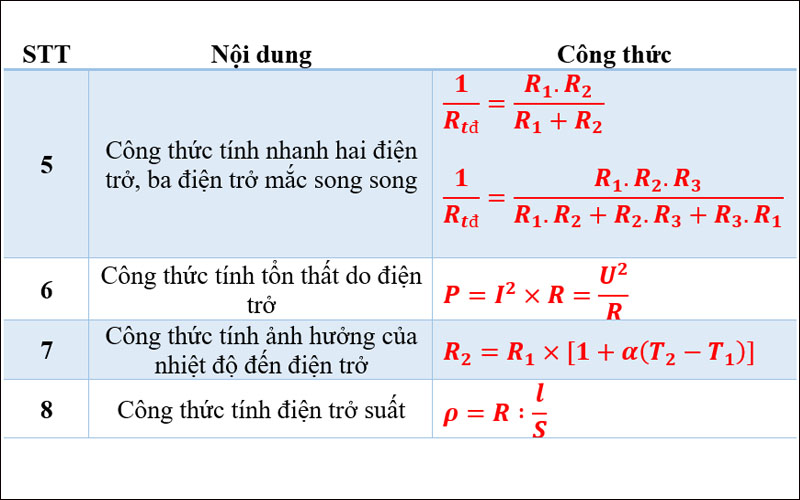
1. Công Thức Cơ Bản
Điện trở suất của một vật liệu có thể được tính theo công thức:
Trong đó:
- \( \rho \): Điện trở suất của vật liệu (\( \Omega \cdot m \))
- \( R \): Điện trở của đoạn dây dẫn (\( \Omega \))
- \( S \): Tiết diện của dây dẫn (\( m^2 \))
- \( l \): Chiều dài dây dẫn (\( m \))
2. Sự Phụ Thuộc Của Điện Trở Suất Vào Nhiệt Độ
Điện trở suất của một số vật liệu thay đổi theo nhiệt độ và có thể được tính bằng công thức:
Trong đó:
- \( \rho_0 \): Điện trở suất tại nhiệt độ ban đầu \( t_0 \) (\( \Omega \cdot m \))
- \( \alpha \): Hệ số nhiệt điện trở (\( K^{-1} \))
- \( t \): Nhiệt độ hiện tại (\( ^\circ C \))
- \( t_0 \): Nhiệt độ ban đầu (\( ^\circ C \))
3. Bảng Điện Trở Suất Của Một Số Kim Loại Tại 20°C
| Kim Loại | Điện Trở Suất \( \rho \) (\( \Omega \cdot m \)) |
|---|---|
| Bạc | 1,6 × 10-8 |
| Đồng | 1,7 × 10-8 |
| Nhôm | 2,8 × 10-8 |
| Vonfram | 5,5 × 10-8 |
| Sắt | 12,0 × 10-8 |
4. Ứng Dụng Thực Tiễn Của Điện Trở Suất
Điện trở suất được ứng dụng rộng rãi trong việc thiết kế và chế tạo các thiết bị điện tử, đặc biệt là trong việc lựa chọn vật liệu làm dây dẫn, mạch điện và các linh kiện điện tử. Hiểu rõ về điện trở suất giúp tối ưu hóa hiệu suất hoạt động và độ bền của các thiết bị này.
5. Ví Dụ Tính Toán Thực Tiễn
Ví dụ, để tính chiều dài tối đa của một dây dẫn đồng có điện trở không vượt quá 10 \( \Omega \), với bán kính tiết diện 0,725 mm, ta có thể sử dụng công thức trên để xác định chiều dài dây:
Áp dụng các giá trị cụ thể để tìm ra chiều dài tối ưu của dây dẫn.
Kết Luận
Việc hiểu và ứng dụng các công thức tính điện trở suất là vô cùng quan trọng trong lĩnh vực điện tử và kỹ thuật. Các công thức này không chỉ giúp hiểu rõ hơn về tính chất của vật liệu mà còn hỗ trợ trong việc thiết kế, chế tạo các thiết bị điện hiệu quả hơn.
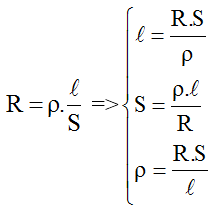
.png)
1. Giới Thiệu Về Điện Trở Suất
Điện trở suất, ký hiệu là \( \rho \), là một đại lượng vật lý quan trọng trong lĩnh vực điện học, dùng để đo khả năng cản trở dòng điện của một vật liệu. Điện trở suất được định nghĩa là điện trở của một đoạn vật liệu có chiều dài nhất định và tiết diện đồng đều.
Điện trở suất phụ thuộc chủ yếu vào bản chất của vật liệu và được xác định bằng công thức:
Trong đó:
- \( \rho \) là điện trở suất (\( \Omega \cdot m \))
- \( R \) là điện trở (\( \Omega \)) của đoạn vật liệu
- \( S \) là tiết diện ngang của vật liệu (\( m^2 \))
- \( l \) là chiều dài của vật liệu (\( m \))
Mỗi vật liệu khác nhau có điện trở suất khác nhau, và điện trở suất của một vật liệu cụ thể có thể thay đổi khi nhiệt độ thay đổi. Chẳng hạn, đối với kim loại, điện trở suất thường tăng khi nhiệt độ tăng.
Điện trở suất là một yếu tố quan trọng trong việc thiết kế và lựa chọn vật liệu cho các thiết bị điện tử, đảm bảo hiệu suất và an toàn cho các ứng dụng điện trong thực tế. Việc hiểu rõ về điện trở suất giúp trong việc dự đoán và điều chỉnh điện trở của các thành phần trong mạch điện, từ đó tối ưu hóa hiệu quả hoạt động của hệ thống.
2. Công Thức Tính Điện Trở Suất
Điện trở suất của một vật liệu là một đại lượng quan trọng trong việc xác định tính chất dẫn điện của vật liệu đó. Dưới đây là các công thức tính điện trở suất, được sử dụng phổ biến trong vật lý và kỹ thuật.
2.1 Công Thức Cơ Bản Tính Điện Trở Suất
Công thức cơ bản để tính điện trở suất của một vật liệu được cho bởi:
Trong đó:
- \( \rho \): Điện trở suất (\( \Omega \cdot m \))
- \( R \): Điện trở của vật liệu (\( \Omega \))
- \( S \): Tiết diện ngang của vật liệu (\( m^2 \))
- \( l \): Chiều dài của vật liệu (\( m \))
2.2 Công Thức Tính Điện Trở Suất Phụ Thuộc Nhiệt Độ
Điện trở suất của hầu hết các vật liệu thay đổi khi nhiệt độ thay đổi. Công thức tính điện trở suất theo nhiệt độ được biểu diễn như sau:
Trong đó:
- \( \rho_0 \): Điện trở suất tại nhiệt độ tham chiếu \( T_0 \) (\( \Omega \cdot m \))
- \( \alpha \): Hệ số nhiệt điện trở (\( K^{-1} \))
- \( T \): Nhiệt độ hiện tại (\( ^\circ C \))
- \( T_0 \): Nhiệt độ tham chiếu (\( ^\circ C \))
2.3 Công Thức Tính Điện Trở Suất Của Kim Loại
Trong các kim loại, điện trở suất thường tăng khi nhiệt độ tăng. Công thức tính điện trở suất của kim loại thường được biểu diễn dưới dạng:
Điều này có nghĩa là khi nhiệt độ tăng, các nguyên tử kim loại dao động mạnh hơn, gây cản trở nhiều hơn cho dòng điện tử, do đó làm tăng điện trở suất.
2.4 Công Thức Tính Điện Trở Suất Của Bán Dẫn
Trong các vật liệu bán dẫn, điện trở suất có sự phụ thuộc phức tạp vào nhiệt độ và nồng độ tạp chất. Một công thức đơn giản hóa có thể được viết như:
Trong đó:
- \( q \): Điện tích của electron (\( C \))
- \( n \): Nồng độ hạt tải điện tử (\( m^{-3} \))
- \( p \): Nồng độ hạt tải lỗ trống (\( m^{-3} \))
- \( \mu_n \): Độ linh động của điện tử (\( m^2/Vs \))
- \( \mu_p \): Độ linh động của lỗ trống (\( m^2/Vs \))
Điện trở suất của vật liệu bán dẫn giảm khi nhiệt độ tăng, điều này khác với kim loại.
Những công thức này là cơ sở để hiểu và dự đoán hành vi của các vật liệu trong mạch điện, giúp các kỹ sư và nhà khoa học thiết kế các thiết bị điện tử hiệu quả hơn.

3. Bảng Điện Trở Suất Của Một Số Vật Liệu
Điện trở suất của các vật liệu khác nhau là một yếu tố quan trọng trong việc thiết kế và sử dụng các thành phần điện tử. Bảng dưới đây liệt kê điện trở suất của một số vật liệu phổ biến, giúp bạn hiểu rõ hơn về tính chất điện của chúng.
| Vật Liệu | Điện Trở Suất (\( \Omega \cdot m \)) |
|---|---|
| Đồng (Cu) | \(1.68 \times 10^{-8}\) |
| Nhôm (Al) | \(2.82 \times 10^{-8}\) |
| Bạc (Ag) | \(1.59 \times 10^{-8}\) |
| Vàng (Au) | \(2.44 \times 10^{-8}\) |
| Thép (Steel) | \(1.0 \times 10^{-7}\) |
| Sắt (Fe) | \(9.71 \times 10^{-8}\) |
| Chì (Pb) | \(2.2 \times 10^{-7}\) |
| Thủy Ngân (Hg) | \(9.58 \times 10^{-7}\) |
| Carbon (C, dạng than chì) | \(3.5 \times 10^{-5}\) |
| Silicon (Si, bán dẫn loại N) | \(6.40 \times 10^{-2}\) |
| Germanium (Ge, bán dẫn loại N) | \(4.6 \times 10^{-1}\) |
Bảng này cung cấp một cái nhìn tổng quan về điện trở suất của các vật liệu, từ kim loại dẫn điện tốt như đồng và bạc đến các chất bán dẫn như silicon và germanium. Khi thiết kế các mạch điện hoặc các thiết bị điện tử, việc lựa chọn vật liệu với điện trở suất phù hợp là rất quan trọng để đảm bảo hiệu suất hoạt động tối ưu.

4. Ứng Dụng Của Điện Trở Suất
Điện trở suất là một đại lượng quan trọng trong nhiều lĩnh vực kỹ thuật và công nghệ, đặc biệt là trong thiết kế và sản xuất các thiết bị điện tử. Dưới đây là một số ứng dụng nổi bật của điện trở suất:
4.1 Thiết Kế Và Chế Tạo Dây Dẫn Điện
Điện trở suất của vật liệu đóng vai trò quan trọng trong việc lựa chọn vật liệu làm dây dẫn điện. Các vật liệu có điện trở suất thấp, như đồng và nhôm, thường được sử dụng để chế tạo dây dẫn điện do khả năng dẫn điện tốt và tổn thất năng lượng thấp.
4.2 Cảm Biến Nhiệt Độ
Các cảm biến nhiệt độ, như nhiệt điện trở (RTD), dựa vào sự thay đổi điện trở suất của vật liệu theo nhiệt độ. Điện trở suất của vật liệu sẽ thay đổi khi nhiệt độ thay đổi, cho phép đo lường nhiệt độ thông qua thay đổi điện trở của cảm biến.
4.3 Ứng Dụng Trong Bán Dẫn
Điện trở suất của vật liệu bán dẫn, như silicon và germanium, có thể điều chỉnh thông qua việc pha tạp để tạo ra các linh kiện điện tử như diode, transistor và vi mạch. Điều này cho phép kiểm soát dòng điện trong các thiết bị điện tử một cách hiệu quả.
4.4 Thiết Kế Hệ Thống Sưởi Ấm
Các vật liệu có điện trở suất cao thường được sử dụng trong các thiết bị sưởi ấm, chẳng hạn như dây điện trở trong lò sưởi hoặc máy nước nóng. Khi dòng điện chạy qua, chúng sinh nhiệt do điện trở suất cao, giúp biến đổi điện năng thành nhiệt năng.
4.5 Ứng Dụng Trong Đo Lường Và Kiểm Tra
Điện trở suất cũng được sử dụng để kiểm tra chất lượng vật liệu và phát hiện các khuyết tật trong sản xuất. Ví dụ, trong kỹ thuật kiểm tra không phá hủy (NDT), sự thay đổi điện trở suất có thể chỉ ra các khuyết tật bên trong vật liệu.
Những ứng dụng này chỉ là một phần nhỏ trong vô số các ứng dụng thực tế của điện trở suất trong đời sống và công nghiệp, giúp nâng cao hiệu suất, an toàn và chất lượng của các sản phẩm điện tử và hệ thống điện.

5. Các Ví Dụ Tính Toán Điện Trở Suất Thực Tế
Để hiểu rõ hơn về cách áp dụng các công thức tính điện trở suất vào thực tế, dưới đây là một số ví dụ minh họa cụ thể. Những ví dụ này sẽ giúp bạn nắm vững phương pháp tính toán và ứng dụng điện trở suất trong các trường hợp khác nhau.
5.1 Ví Dụ 1: Tính Điện Trở Suất Của Một Dây Dẫn Đồng
Giả sử chúng ta có một dây dẫn đồng với chiều dài \( l = 2 \, \text{m} \) và tiết diện ngang \( S = 1 \times 10^{-6} \, \text{m}^2 \). Điện trở của dây dẫn này được đo là \( R = 3.36 \times 10^{-2} \, \Omega \). Điện trở suất của dây dẫn đồng được tính như sau:
Điều này cho thấy điện trở suất của đồng phù hợp với giá trị tiêu chuẩn, chứng minh tính chính xác của phép tính.
5.2 Ví Dụ 2: Tính Điện Trở Suất Của Một Vật Liệu Kim Loại Ở Nhiệt Độ Cao
Một dây dẫn làm từ nhôm có chiều dài \( l = 5 \, \text{m} \) và tiết diện ngang \( S = 2 \times 10^{-6} \, \text{m}^2 \). Ở nhiệt độ \( T_0 = 20^\circ \text{C} \), điện trở suất của nhôm là \( \rho_0 = 2.82 \times 10^{-8} \, \Omega \cdot m \). Hệ số nhiệt điện trở của nhôm là \( \alpha = 3.9 \times 10^{-3} \, K^{-1} \). Tính điện trở suất của nhôm ở nhiệt độ \( T = 100^\circ \text{C} \).
Áp dụng công thức:
Điện trở suất của nhôm tăng lên khi nhiệt độ tăng, điều này phù hợp với tính chất của kim loại.
5.3 Ví Dụ 3: Tính Điện Trở Suất Của Một Bán Dẫn
Xét một mẫu silicon có nồng độ hạt tải điện tử \( n = 1.5 \times 10^{16} \, \text{m}^{-3} \) và lỗ trống \( p = 1.5 \times 10^{10} \, \text{m}^{-3} \). Độ linh động của điện tử \( \mu_n = 0.135 \, \text{m}^2/Vs \) và của lỗ trống \( \mu_p = 0.048 \, \text{m}^2/Vs \). Tính điện trở suất của mẫu silicon.
Trong đó, \( q = 1.6 \times 10^{-19} \, C \) là điện tích của electron.
Kết quả này cho thấy cách tính điện trở suất của một bán dẫn như silicon dựa trên các tham số cơ bản.
XEM THÊM:
6. Kết Luận
Trong bài viết này, chúng ta đã cùng tìm hiểu về các công thức tính điện trở suất và những ứng dụng của chúng trong nhiều lĩnh vực khác nhau. Dưới đây là những điểm quan trọng cần lưu ý:
6.1 Tóm Tắt Các Công Thức Quan Trọng
- Công thức cơ bản: Điện trở suất \(\rho\) được tính theo công thức: \[ \rho = R \cdot \frac{S}{L} \] trong đó, \(R\) là điện trở (Ohm), \(S\) là tiết diện (m²) và \(L\) là chiều dài dây dẫn (m).
- Điện trở suất theo nhiệt độ: Khi nhiệt độ thay đổi, điện trở suất được điều chỉnh theo công thức: \[ \rho = \rho_0 \cdot \left(1 + \alpha \cdot \Delta t\right) \] trong đó, \(\rho_0\) là điện trở suất tại nhiệt độ ban đầu, \(\alpha\) là hệ số nhiệt điện trở và \(\Delta t\) là sự thay đổi nhiệt độ.
6.2 Những Điều Cần Lưu Ý Khi Tính Toán Điện Trở Suất
- Điện trở suất là một đại lượng vật lý đặc trưng cho từng loại vật liệu, nó phản ánh khả năng cản trở dòng điện của vật liệu đó.
- Cần phải lưu ý đến nhiệt độ khi tính toán điện trở suất, đặc biệt là trong các ứng dụng yêu cầu độ chính xác cao, vì nhiệt độ ảnh hưởng trực tiếp đến giá trị của điện trở suất.
- Chọn vật liệu có điện trở suất phù hợp với yêu cầu cụ thể của ứng dụng để đảm bảo hiệu quả sử dụng và tiết kiệm năng lượng.
Hi vọng rằng với các kiến thức và công thức được chia sẻ trong bài viết này, bạn đọc có thể áp dụng chúng một cách hiệu quả trong học tập cũng như thực tế. Điện trở suất không chỉ là một khái niệm cơ bản trong vật lý mà còn là nền tảng cho nhiều ứng dụng công nghệ hiện đại.