Chủ đề công thức tính điện trở suất theo nhiệt độ: Công thức tính điện trở suất theo nhiệt độ là một khái niệm quan trọng trong lĩnh vực vật lý và kỹ thuật điện. Bài viết này cung cấp hướng dẫn chi tiết về cách sử dụng công thức này, giải thích các yếu tố ảnh hưởng, và ứng dụng thực tế trong thiết kế mạch điện và các thiết bị điện tử.
Mục lục
- Công thức tính điện trở suất theo nhiệt độ
- 1. Khái niệm về điện trở suất và nhiệt độ
- 2. Công thức tính điện trở suất theo nhiệt độ
- 3. Hệ số nhiệt điện trở (\(\alpha\)) và vai trò của nó
- 4. Ứng dụng của công thức trong thực tế
- 5. Ví dụ tính toán điện trở suất theo nhiệt độ
- 6. Lưu ý khi tính toán điện trở suất theo nhiệt độ
- 7. Kết luận
Công thức tính điện trở suất theo nhiệt độ
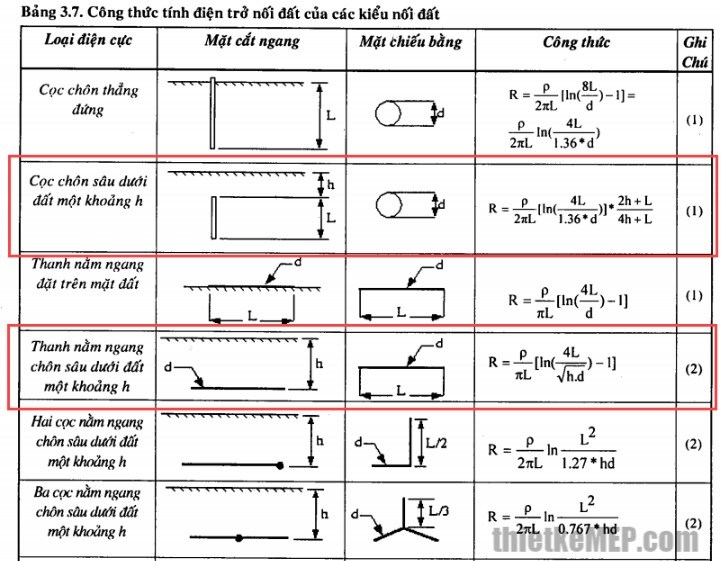
Điện trở suất (\(\rho\)) của một vật liệu là một đại lượng vật lý biểu thị khả năng cản trở dòng điện của vật liệu đó. Điện trở suất của một vật liệu phụ thuộc vào nhiệt độ và có thể thay đổi khi nhiệt độ thay đổi. Công thức tính điện trở suất theo nhiệt độ thường được sử dụng trong các ứng dụng khoa học và kỹ thuật để dự đoán sự thay đổi của điện trở suất khi nhiệt độ thay đổi.
Công thức tổng quát
Công thức tính điện trở suất của vật liệu kim loại theo nhiệt độ có dạng:
Trong đó:
- \(\rho(T)\): Điện trở suất tại nhiệt độ \(T\) (đơn vị: ohm mét, Ω·m).
- \(\rho_0\): Điện trở suất tại nhiệt độ tham chiếu \(T_0\) (thường là 20°C hoặc 25°C).
- \(\alpha\): Hệ số nhiệt điện trở, biểu thị sự thay đổi điện trở suất khi nhiệt độ thay đổi (đơn vị: 1/°C).
- \(T\): Nhiệt độ tại thời điểm tính toán (đơn vị: °C).
- \(T_0\): Nhiệt độ tham chiếu (đơn vị: °C).
Ý nghĩa của công thức
Công thức trên cho thấy rằng điện trở suất của vật liệu sẽ tăng lên khi nhiệt độ tăng nếu hệ số nhiệt điện trở \(\alpha\) dương (điều này thường đúng với hầu hết các kim loại). Ngược lại, nếu \(\alpha\) âm, điện trở suất sẽ giảm khi nhiệt độ tăng (điều này thường xảy ra ở các vật liệu bán dẫn hoặc vật liệu siêu dẫn).
Các ví dụ về hệ số nhiệt điện trở \(\alpha\)
Hệ số nhiệt điện trở \(\alpha\) khác nhau tùy thuộc vào loại vật liệu. Một số giá trị điển hình bao gồm:
| Vật liệu | Hệ số nhiệt điện trở \(\alpha\) (1/°C) |
|---|---|
| Đồng (Cu) | 0.00393 |
| Nhôm (Al) | 0.00429 |
| Bạc (Ag) | 0.0038 |
| Sắt (Fe) | 0.00651 |
Cách áp dụng công thức
Để sử dụng công thức này trong thực tế, bạn cần biết điện trở suất ban đầu \(\rho_0\) của vật liệu ở nhiệt độ tham chiếu \(T_0\) và hệ số nhiệt điện trở \(\alpha\) của vật liệu. Sau đó, khi biết nhiệt độ \(T\) tại thời điểm cần tính toán, bạn có thể sử dụng công thức để tính điện trở suất tại nhiệt độ đó.
Ứng dụng thực tế
Việc hiểu và tính toán điện trở suất theo nhiệt độ là rất quan trọng trong thiết kế mạch điện và điện tử, đặc biệt trong các ứng dụng đòi hỏi độ chính xác cao như cảm biến nhiệt độ, thiết bị điện trở chính xác, và các hệ thống đo lường. Bằng cách sử dụng công thức trên, kỹ sư và nhà khoa học có thể dự đoán và điều chỉnh hiệu suất của các thiết bị này theo điều kiện nhiệt độ thay đổi.
.png)
1. Khái niệm về điện trở suất và nhiệt độ
Điện trở suất (\(\rho\)) là một đại lượng vật lý biểu thị khả năng của một vật liệu cản trở dòng điện chạy qua nó. Nó phụ thuộc vào bản chất của vật liệu và điều kiện môi trường như nhiệt độ. Khi nhiệt độ thay đổi, điện trở suất của một vật liệu cũng thay đổi, đặc biệt là đối với các kim loại và chất bán dẫn.
Điện trở suất của một vật liệu được xác định theo công thức:
Trong đó:
- \(\rho\): Điện trở suất (đơn vị: ohm mét, Ω·m)
- \(R\): Điện trở của vật dẫn điện (đơn vị: ohm, Ω)
- \(A\): Diện tích mặt cắt ngang của vật dẫn điện (đơn vị: mét vuông, m²)
- \(L\): Chiều dài của vật dẫn điện (đơn vị: mét, m)
Nhiệt độ là một yếu tố quan trọng ảnh hưởng đến điện trở suất của vật liệu. Ở hầu hết các vật liệu dẫn điện như kim loại, khi nhiệt độ tăng, điện trở suất cũng tăng. Điều này là do khi nhiệt độ tăng, các ion trong vật liệu dao động mạnh hơn, làm tăng sự va chạm của các electron di chuyển qua vật liệu, gây ra sự cản trở lớn hơn cho dòng điện.
Ngược lại, trong các vật liệu bán dẫn như silicon hoặc germanium, điện trở suất có thể giảm khi nhiệt độ tăng. Điều này xảy ra vì khi nhiệt độ tăng, số lượng electron tự do trong vật liệu tăng, làm giảm điện trở suất tổng thể.
Đối với một số vật liệu đặc biệt, như siêu dẫn, điện trở suất có thể giảm xuống gần bằng không ở nhiệt độ rất thấp, cho phép dòng điện chạy qua mà không gặp phải bất kỳ sự cản trở đáng kể nào.
Tóm lại, điện trở suất và nhiệt độ có mối quan hệ mật thiết với nhau, và sự thay đổi nhiệt độ có thể ảnh hưởng lớn đến khả năng dẫn điện của một vật liệu. Hiểu rõ về mối quan hệ này là rất quan trọng trong việc thiết kế các thiết bị điện tử và ứng dụng kỹ thuật khác.
2. Công thức tính điện trở suất theo nhiệt độ
Điện trở suất của một vật liệu thay đổi theo nhiệt độ, và mối quan hệ này thường được mô tả bằng công thức toán học. Đối với hầu hết các vật liệu dẫn điện, đặc biệt là kim loại, điện trở suất tăng lên khi nhiệt độ tăng. Công thức phổ biến nhất để tính điện trở suất (\(\rho\)) của một vật liệu tại một nhiệt độ nhất định được biểu diễn như sau:
Trong đó:
- \(\rho(T)\): Điện trở suất tại nhiệt độ \(T\) (đơn vị: ohm mét, Ω·m).
- \(\rho_0\): Điện trở suất tại nhiệt độ tham chiếu \(T_0\) (thường là 20°C hoặc 25°C).
- \(\alpha\): Hệ số nhiệt điện trở, một hằng số biểu thị mức độ thay đổi của điện trở suất khi nhiệt độ thay đổi (đơn vị: 1/°C).
- \(T\): Nhiệt độ cần tính toán (đơn vị: °C).
- \(T_0\): Nhiệt độ tham chiếu (đơn vị: °C).
Công thức này chỉ ra rằng điện trở suất của vật liệu sẽ thay đổi tỷ lệ với sự thay đổi nhiệt độ từ nhiệt độ tham chiếu. Hệ số nhiệt điện trở \(\alpha\) thường có giá trị dương đối với kim loại, do đó điện trở suất tăng khi nhiệt độ tăng.
Các bước tính toán điện trở suất theo nhiệt độ:
- Xác định điện trở suất ban đầu \(\rho_0\) tại nhiệt độ tham chiếu \(T_0\). Giá trị này thường có thể được tìm thấy trong các bảng dữ liệu vật liệu.
- Xác định hệ số nhiệt điện trở \(\alpha\) của vật liệu. Giá trị này cũng có sẵn trong các bảng dữ liệu và thường được xác định qua các thí nghiệm.
- Xác định nhiệt độ hiện tại \(T\) mà bạn muốn tính toán điện trở suất.
- Sử dụng công thức \(\rho(T) = \rho_0 (1 + \alpha (T - T_0))\) để tính toán điện trở suất tại nhiệt độ \(T\).
Ví dụ tính toán:
Giả sử chúng ta có một đoạn dây đồng với:
- \(\rho_0 = 1.68 \times 10^{-8}\) Ω·m tại \(T_0 = 20°C\).
- \(\alpha = 0.00393 \, \text{°C}^{-1}\) đối với đồng.
- Nhiệt độ cần tính toán \(T = 100°C\).
Áp dụng công thức:
Điện trở suất của dây đồng tại 100°C sẽ là \(2.21 \times 10^{-8} \, \Omega \cdot m\).
Như vậy, công thức tính điện trở suất theo nhiệt độ rất hữu ích trong việc dự đoán sự thay đổi của điện trở suất vật liệu khi nhiệt độ thay đổi, đặc biệt trong các ứng dụng kỹ thuật và thiết kế điện tử.

3. Hệ số nhiệt điện trở (\(\alpha\)) và vai trò của nó
Hệ số nhiệt điện trở (\(\alpha\)) là một tham số quan trọng trong công thức tính điện trở suất của vật liệu theo nhiệt độ. Nó biểu thị mức độ thay đổi của điện trở suất khi nhiệt độ thay đổi. Hiểu rõ về hệ số này giúp chúng ta dự đoán chính xác sự thay đổi của điện trở suất khi nhiệt độ của vật liệu thay đổi, từ đó tối ưu hóa thiết kế trong các ứng dụng điện tử và kỹ thuật.
Hệ số nhiệt điện trở được xác định bằng công thức:
Trong đó:
- \(\Delta \rho\): Sự thay đổi điện trở suất của vật liệu (đơn vị: Ω·m).
- \(\rho_0\): Điện trở suất của vật liệu tại nhiệt độ tham chiếu \(T_0\) (đơn vị: Ω·m).
- \(\Delta T\): Sự thay đổi nhiệt độ (đơn vị: °C).
Vai trò của hệ số nhiệt điện trở (\(\alpha\))
Hệ số nhiệt điện trở đóng vai trò quan trọng trong việc xác định tính chất dẫn điện của vật liệu trong các điều kiện nhiệt độ khác nhau:
- Dự đoán sự thay đổi điện trở suất: Hệ số \(\alpha\) cho phép chúng ta dự đoán sự thay đổi của điện trở suất khi nhiệt độ thay đổi. Điều này quan trọng đối với các thiết bị điện tử hoạt động ở các nhiệt độ khác nhau, giúp đảm bảo hiệu suất và độ tin cậy của thiết bị.
- Thiết kế và lựa chọn vật liệu: Biết được \(\alpha\) của một vật liệu giúp kỹ sư chọn đúng loại vật liệu phù hợp cho một ứng dụng cụ thể, đảm bảo tính ổn định và hiệu quả của mạch điện dưới các điều kiện nhiệt độ khác nhau.
- Tối ưu hóa hiệu suất nhiệt: Trong các ứng dụng cần kiểm soát nhiệt độ, như trong các cảm biến nhiệt hoặc bộ điều khiển nhiệt độ, hiểu rõ hệ số nhiệt điện trở giúp cải thiện hiệu suất hoạt động và tăng cường độ chính xác của thiết bị.
Ví dụ về các giá trị hệ số nhiệt điện trở (\(\alpha\)) của một số vật liệu
| Vật liệu | Hệ số nhiệt điện trở \(\alpha\) (1/°C) |
|---|---|
| Đồng (Cu) | 0.00393 |
| Nhôm (Al) | 0.00429 |
| Bạc (Ag) | 0.0038 |
| Vàng (Au) | 0.0034 |
| Silicon (Si) | -0.075 |
Các giá trị trong bảng trên cho thấy rằng hệ số nhiệt điện trở có thể khác nhau đáng kể giữa các vật liệu. Đối với kim loại như đồng, nhôm và bạc, \(\alpha\) dương, cho thấy điện trở suất tăng khi nhiệt độ tăng. Tuy nhiên, đối với chất bán dẫn như silicon, \(\alpha\) âm, chỉ ra rằng điện trở suất giảm khi nhiệt độ tăng. Đây là những đặc tính quan trọng cần được xem xét khi thiết kế các thiết bị điện tử.
Như vậy, hệ số nhiệt điện trở (\(\alpha\)) không chỉ giúp chúng ta hiểu rõ hơn về tính chất điện của vật liệu mà còn đóng vai trò quan trọng trong việc thiết kế và tối ưu hóa các thiết bị và mạch điện tử hoạt động dưới nhiều điều kiện nhiệt độ khác nhau.
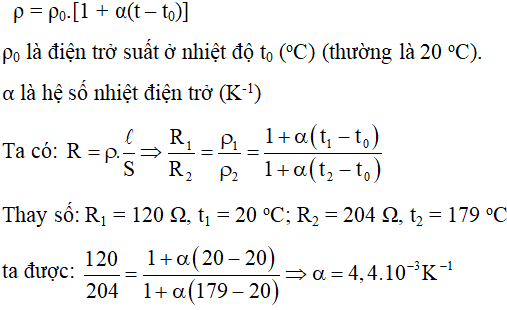
4. Ứng dụng của công thức trong thực tế
Công thức tính điện trở suất theo nhiệt độ được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ thiết kế thiết bị điện tử đến nghiên cứu khoa học và công nghiệp. Việc hiểu rõ cách thức thay đổi điện trở suất theo nhiệt độ giúp kỹ sư và nhà khoa học tối ưu hóa các hệ thống điện và đảm bảo hoạt động hiệu quả trong các điều kiện môi trường khác nhau.
4.1. Thiết kế mạch điện và thiết bị điện tử
Trong thiết kế mạch điện và các thiết bị điện tử, đặc biệt là các thiết bị nhạy cảm với nhiệt độ như cảm biến nhiệt độ và bộ vi xử lý, việc tính toán điện trở suất theo nhiệt độ là vô cùng quan trọng. Điều này giúp:
- Dự đoán hiệu suất mạch: Biết được sự thay đổi của điện trở suất theo nhiệt độ giúp dự đoán chính xác hiệu suất của mạch điện khi nhiệt độ môi trường thay đổi.
- Tối ưu hóa thiết kế nhiệt: Các thiết kế tản nhiệt và kiểm soát nhiệt độ có thể được tối ưu hóa để đảm bảo các thành phần hoạt động trong phạm vi nhiệt độ an toàn và hiệu quả.
- Đảm bảo độ tin cậy: Việc hiểu rõ các đặc tính nhiệt của vật liệu giúp tăng độ tin cậy của các thiết bị, đặc biệt là trong môi trường khắc nghiệt hoặc thay đổi nhiệt độ lớn.
4.2. Công nghiệp và sản xuất
Trong ngành công nghiệp, đặc biệt là trong sản xuất các linh kiện điện tử và thiết bị điện, việc tính toán điện trở suất theo nhiệt độ có nhiều ứng dụng thực tế:
- Kiểm tra chất lượng: Trong quá trình sản xuất dây dẫn điện, cần kiểm tra và đảm bảo rằng dây dẫn có điện trở suất phù hợp ở các nhiệt độ làm việc khác nhau để đảm bảo an toàn và hiệu suất.
- Điều khiển quá trình: Nhiều quy trình sản xuất yêu cầu kiểm soát nhiệt độ chặt chẽ để đảm bảo chất lượng sản phẩm cuối cùng. Công thức tính điện trở suất giúp theo dõi và điều chỉnh nhiệt độ trong quá trình sản xuất.
4.3. Nghiên cứu khoa học và giáo dục
Trong nghiên cứu khoa học và giáo dục, công thức tính điện trở suất theo nhiệt độ được sử dụng để giảng dạy và nghiên cứu về tính chất điện và nhiệt của vật liệu:
- Nghiên cứu vật liệu mới: Các nhà khoa học nghiên cứu các vật liệu mới và cần hiểu rõ tính chất điện của chúng dưới các điều kiện nhiệt độ khác nhau để phát triển các vật liệu tiên tiến.
- Giáo dục: Trong giảng dạy vật lý và kỹ thuật, công thức này được sử dụng để giải thích các hiện tượng liên quan đến điện trở suất và nhiệt độ, giúp sinh viên hiểu rõ hơn về các khái niệm cơ bản của điện và nhiệt.
4.4. Ứng dụng trong các thiết bị đo lường và cảm biến
Công thức tính điện trở suất theo nhiệt độ còn được ứng dụng trong các thiết bị đo lường và cảm biến, đặc biệt là các cảm biến nhiệt độ (RTD - Resistance Temperature Detector):
- Cảm biến nhiệt độ: RTD sử dụng sự thay đổi điện trở của vật liệu dẫn điện theo nhiệt độ để đo nhiệt độ một cách chính xác. Công thức tính điện trở suất giúp hiệu chỉnh và tối ưu hóa độ chính xác của các cảm biến này.
- Thiết bị đo lường công nghiệp: Trong các hệ thống đo lường công nghiệp, việc sử dụng công thức này giúp kiểm soát quá trình và đảm bảo các thiết bị đo lường hoạt động chính xác trong điều kiện nhiệt độ thay đổi.
Như vậy, công thức tính điện trở suất theo nhiệt độ có vai trò rất quan trọng trong nhiều lĩnh vực thực tế, từ thiết kế và sản xuất thiết bị điện tử đến nghiên cứu khoa học và giáo dục. Hiểu rõ và áp dụng đúng công thức này giúp cải thiện hiệu suất, độ tin cậy và độ chính xác của các thiết bị và hệ thống điện trong môi trường đa dạng.

5. Ví dụ tính toán điện trở suất theo nhiệt độ
Để hiểu rõ hơn về cách tính điện trở suất theo nhiệt độ, chúng ta sẽ thực hiện một ví dụ cụ thể. Hãy xem xét một dây dẫn bằng đồng có điện trở suất ban đầu \(\rho_0 = 1.68 \times 10^{-8}\) Ω·m ở nhiệt độ \(T_0 = 20^\circ C\). Hệ số nhiệt điện trở của đồng là \(\alpha = 0.00393 \, (1/^\circ C)\). Chúng ta cần tính điện trở suất \(\rho\) của dây dẫn này ở nhiệt độ \(T = 80^\circ C\).
5.1. Công thức tính điện trở suất theo nhiệt độ
Điện trở suất \(\rho\) của một vật liệu ở nhiệt độ \(T\) được tính bằng công thức:
Trong đó:
- \(\rho\): Điện trở suất tại nhiệt độ \(T\) (Ω·m).
- \(\rho_0\): Điện trở suất tại nhiệt độ tham chiếu \(T_0\) (Ω·m).
- \(\alpha\): Hệ số nhiệt điện trở (1/°C).
- \(\Delta T = T - T_0\): Sự chênh lệch nhiệt độ (°C).
5.2. Các bước tính toán cụ thể
- Tính sự chênh lệch nhiệt độ (\(\Delta T\)):
Chúng ta tính \(\Delta T\) như sau:
\[ \Delta T = T - T_0 = 80^\circ C - 20^\circ C = 60^\circ C \] - Áp dụng công thức tính điện trở suất:
Thay các giá trị vào công thức tính \(\rho\):
\[ \rho = \rho_0 (1 + \alpha \Delta T) = 1.68 \times 10^{-8} \, \Omega\cdot m \times (1 + 0.00393 \times 60) \] - Thực hiện các phép tính:
Trước hết, tính giá trị trong ngoặc đơn:
\[ 1 + 0.00393 \times 60 = 1 + 0.2358 = 1.2358 \]Sau đó, tính giá trị của \(\rho\):
\[ \rho = 1.68 \times 10^{-8} \times 1.2358 = 2.075 \times 10^{-8} \, \Omega\cdot m \]
5.3. Kết quả và ý nghĩa
Vậy, điện trở suất của dây dẫn đồng tại nhiệt độ \(80^\circ C\) là \(\rho = 2.075 \times 10^{-8} \, \Omega\cdot m\). Kết quả này cho thấy rằng điện trở suất của vật liệu dẫn điện tăng lên khi nhiệt độ tăng, điều này phù hợp với tính chất vật lý của hầu hết các kim loại. Việc hiểu rõ và có khả năng tính toán điện trở suất tại các nhiệt độ khác nhau giúp đảm bảo rằng các thiết bị và hệ thống điện hoạt động ổn định và an toàn trong nhiều điều kiện môi trường khác nhau.
Qua ví dụ này, chúng ta đã thấy rõ cách ứng dụng công thức tính điện trở suất theo nhiệt độ trong thực tế, từ đó có thể dễ dàng áp dụng vào các tình huống khác nhau trong công nghiệp, nghiên cứu và thiết kế điện tử.
XEM THÊM:
6. Lưu ý khi tính toán điện trở suất theo nhiệt độ
Khi tính toán điện trở suất theo nhiệt độ, có một số lưu ý quan trọng mà chúng ta cần phải xem xét để đảm bảo tính chính xác của kết quả và áp dụng đúng trong các tình huống thực tế. Dưới đây là những điểm cần lưu ý:
6.1. Độ chính xác của các tham số đầu vào
- Hệ số nhiệt điện trở (\(\alpha\)): Hệ số này có thể thay đổi tùy theo vật liệu và điều kiện cụ thể. Đảm bảo sử dụng giá trị \(\alpha\) phù hợp với vật liệu và điều kiện làm việc cụ thể của bài toán.
- Điện trở suất ban đầu (\(\rho_0\)): Giá trị này thường được đo ở nhiệt độ chuẩn, thường là \(20^\circ C\) hoặc \(25^\circ C\). Sử dụng đúng giá trị ban đầu để tránh sai số trong tính toán.
6.2. Ảnh hưởng của nhiệt độ tới vật liệu
- Giới hạn nhiệt độ: Công thức tính điện trở suất theo nhiệt độ chủ yếu áp dụng cho khoảng nhiệt độ mà sự thay đổi điện trở suất với nhiệt độ là tuyến tính. Ở nhiệt độ quá cao hoặc quá thấp, mối quan hệ có thể không còn tuyến tính và cần sử dụng các phương pháp khác để tính toán.
- Sự thay đổi cấu trúc vật liệu: Ở nhiệt độ cao, một số vật liệu có thể trải qua sự thay đổi cấu trúc hoặc pha, dẫn đến sự thay đổi đột ngột trong điện trở suất. Ví dụ, các kim loại có thể bị nóng chảy hoặc oxy hóa, làm thay đổi tính chất dẫn điện của chúng.
6.3. Ảnh hưởng của tạp chất và điều kiện môi trường
- Tạp chất trong vật liệu: Sự có mặt của tạp chất có thể ảnh hưởng đáng kể đến điện trở suất của vật liệu. Tạp chất có thể làm tăng hoặc giảm điện trở suất tùy thuộc vào loại và nồng độ của chúng.
- Điều kiện môi trường: Độ ẩm, áp suất và các yếu tố môi trường khác có thể ảnh hưởng đến điện trở suất của vật liệu, đặc biệt là trong các ứng dụng ngoài trời hoặc trong các môi trường khắc nghiệt.
6.4. Sử dụng công thức phù hợp
- Chọn đúng công thức: Đảm bảo rằng công thức được sử dụng phù hợp với loại vật liệu và phạm vi nhiệt độ. Đối với một số vật liệu đặc biệt như bán dẫn, công thức tính toán có thể phức tạp hơn và đòi hỏi sự điều chỉnh thêm.
- Xem xét các điều kiện biên: Khi áp dụng công thức, cần xem xét các điều kiện biên như dòng điện, điện áp và nhiệt độ xung quanh, để đảm bảo kết quả tính toán phản ánh đúng thực tế.
6.5. Kiểm tra và hiệu chỉnh kết quả
- Kiểm tra lại phép tính: Luôn kiểm tra lại các phép tính để đảm bảo không có sai sót trong quá trình tính toán. Đặc biệt chú ý đến các phép nhân, chia và cộng trừ với các số mũ và đơn vị đo lường.
- Hiệu chỉnh kết quả với thực tế: Nếu có thể, so sánh kết quả tính toán với các giá trị thực tế đo được để xác minh tính chính xác của mô hình tính toán.
Việc lưu ý các yếu tố trên sẽ giúp đảm bảo tính chính xác và độ tin cậy của các kết quả tính toán điện trở suất theo nhiệt độ, đồng thời giúp áp dụng công thức một cách hiệu quả trong thực tế.

7. Kết luận
Việc hiểu và áp dụng chính xác công thức tính điện trở suất theo nhiệt độ đóng vai trò vô cùng quan trọng trong nhiều lĩnh vực, từ nghiên cứu khoa học đến ứng dụng thực tế trong công nghiệp và đời sống hàng ngày. Công thức này không chỉ giúp chúng ta dự đoán được sự thay đổi của điện trở suất khi nhiệt độ thay đổi, mà còn hỗ trợ trong việc thiết kế các thiết bị điện tử và mạch điện có độ chính xác cao.
Dưới đây là một số điểm quan trọng cần ghi nhớ:
- Độ chính xác trong tính toán: Để đảm bảo kết quả tính toán chính xác, việc xác định các biến số trong công thức như hệ số nhiệt điện trở (\(\alpha\)), điện trở suất ban đầu (\(\rho_0\)), và nhiệt độ là rất quan trọng. Các giá trị này cần được đo lường cẩn thận hoặc tham khảo từ các nguồn đáng tin cậy.
- Ảnh hưởng của điều kiện môi trường: Ngoài nhiệt độ, các yếu tố môi trường khác như độ ẩm, áp suất cũng có thể ảnh hưởng đến điện trở suất của vật liệu. Do đó, khi ứng dụng công thức này trong thực tế, cần xem xét các điều kiện môi trường để hiệu chỉnh và đảm bảo độ chính xác.
- Ứng dụng trong thực tiễn: Công thức tính điện trở suất theo nhiệt độ có nhiều ứng dụng thực tế quan trọng, từ việc thiết kế các cảm biến nhiệt độ đến sản xuất các thiết bị điện tử có độ chính xác cao. Nhờ vào việc hiểu rõ mối quan hệ giữa nhiệt độ và điện trở suất, các kỹ sư và nhà nghiên cứu có thể cải thiện hiệu suất và độ tin cậy của các thiết bị này.
- Phát triển và nghiên cứu thêm: Công thức này không phải là tĩnh, mà có thể được mở rộng và phát triển thêm với các nghiên cứu mới. Những nghiên cứu về các vật liệu mới hoặc điều kiện đặc biệt có thể dẫn đến việc cải tiến công thức, giúp ứng dụng trong những trường hợp phức tạp hơn.
Tóm lại, công thức tính điện trở suất theo nhiệt độ là một công cụ mạnh mẽ, không chỉ giúp chúng ta hiểu rõ hơn về các tính chất vật lý của vật liệu mà còn hỗ trợ trong việc thiết kế và phát triển các sản phẩm công nghệ cao. Để tận dụng hết tiềm năng của công thức này, việc nghiên cứu và áp dụng đúng đắn là điều cần thiết.







.jpg)