Chủ đề công thức tính điện trở toàn phần: Bài viết này cung cấp một hướng dẫn chi tiết về cách tính điện trở toàn phần trong các mạch điện. Với sự kết hợp của lý thuyết cơ bản và ví dụ minh họa, bài viết sẽ giúp bạn nắm vững các công thức cần thiết để tính toán chính xác điện trở trong các mạch nối tiếp, song song và hỗn hợp, giúp bạn áp dụng dễ dàng vào thực tế.
Mục lục
Công Thức Tính Điện Trở Toàn Phần
Điện trở toàn phần trong một mạch điện có thể được tính toán dựa trên cách các điện trở trong mạch được bố trí: mắc nối tiếp, mắc song song hoặc kết hợp cả hai. Dưới đây là các công thức và phương pháp tính toán cụ thể:
1. Điện Trở Toàn Phần Trong Mạch Nối Tiếp
Trong mạch điện mắc nối tiếp, điện trở toàn phần \(R_t\) là tổng của tất cả các điện trở thành phần:
\[
R_t = R_1 + R_2 + R_3 + \ldots + R_n
\]
Ví dụ, nếu một mạch nối tiếp có ba điện trở \(R_1 = 4 \, \Omega\), \(R_2 = 5 \, \Omega\), và \(R_3 = 6 \, \Omega\), thì điện trở toàn phần sẽ là:
\[
R_t = 4 \, \Omega + 5 \, \Omega + 6 \, \Omega = 15 \, \Omega
\]
2. Điện Trở Toàn Phần Trong Mạch Song Song
Trong mạch điện mắc song song, điện trở toàn phần được tính bằng cách lấy nghịch đảo của tổng nghịch đảo của các điện trở thành phần:
\[
\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}
\]
Ví dụ, nếu một mạch song song có ba điện trở \(R_1 = 2 \, \Omega\), \(R_2 = 3 \, \Omega\), và \(R_3 = 6 \, \Omega\), thì điện trở toàn phần sẽ là:
\[
\frac{1}{R_t} = \frac{1}{2 \, \Omega} + \frac{1}{3 \, \Omega} + \frac{1}{6 \, \Omega} = 1 \, \Omega
\]
Suy ra:
\[
R_t = 1 \, \Omega
\]
3. Điện Trở Toàn Phần Trong Mạch Hỗn Hợp
Mạch hỗn hợp bao gồm cả các điện trở mắc nối tiếp và mắc song song. Để tính điện trở toàn phần của mạch này, ta cần phân chia thành các phần nhỏ, tính toán từng phần rồi kết hợp lại.
Giả sử có một mạch hỗn hợp gồm:
- Điện trở trong của nguồn điện \(r = 0.5 \, \Omega\)
- Hai điện trở mắc nối tiếp: \(R_1 = 2 \, \Omega\) và \(R_2 = 3 \, \Omega\)
- Một điện trở mắc song song với tổng điện trở nối tiếp: \(R_3 = 6 \, \Omega\)
Trước hết, tính tổng điện trở của hai điện trở nối tiếp:
\[
R_s = R_1 + R_2 = 2 \, \Omega + 3 \, \Omega = 5 \, \Omega
\]
Sau đó, tính điện trở tương đương của mạch song song:
\[
\frac{1}{R_p} = \frac{1}{R_3} + \frac{1}{R_s} = \frac{1}{6 \, \Omega} + \frac{1}{5 \, \Omega} = 0.367 \, \Omega
\]
Vậy:
\[
R_p = \frac{1}{0.367 \, \Omega} \approx 2.73 \, \Omega
\]
Cuối cùng, điện trở toàn phần của mạch điện kín bao gồm cả điện trở trong của nguồn điện:
\[
R_t = r + R_p = 0.5 \, \Omega + 2.73 \, \Omega = 3.23 \, \Omega
\]
4. Ảnh Hưởng Của Điện Trở Toàn Phần Đến Mạch Điện
Điện trở toàn phần có vai trò quan trọng trong việc xác định cường độ dòng điện và công suất tiêu thụ trong mạch điện theo định luật Ohm:
\[
I = \frac{V}{R_t}
\]
Trong đó:
- \(I\) là cường độ dòng điện (Ampe)
- \(V\) là hiệu điện thế (Vôn)
- \(R_t\) là điện trở toàn phần (Ohm)
Khi \(R_t\) tăng, cường độ dòng điện giảm và ngược lại. Điều này ảnh hưởng trực tiếp đến hiệu suất và độ bền của các thành phần trong mạch.
5. Bài Tập Thực Hành
Dưới đây là một số bài tập giúp bạn thực hành tính toán điện trở toàn phần của mạch điện:
- Một mạch nối tiếp gồm các điện trở: \(R_1 = 4 \, \Omega\), \(R_2 = 5 \, \Omega\), và \(R_3 = 6 \, \Omega\). Hãy tính điện trở toàn phần của mạch.
- Một mạch song song gồm các điện trở: \(R_1 = 3 \, \Omega\), \(R_2 = 6 \, \Omega\), và \(R_3 = 9 \, \Omega\). Hãy tính điện trở toàn phần của mạch.
- Một mạch hỗn hợp gồm các điện trở: \(R_1 = 2 \, \Omega\) và \(R_2 = 3 \, \Omega\) mắc nối tiếp, kết hợp với \(R_3 = 4 \, \Omega\) mắc song song. Hãy tính điện trở toàn phần của mạch.
Hãy thử giải các bài tập trên và kiểm tra lại với đáp án.

.png)
1. Khái Niệm Cơ Bản về Điện Trở
Điện trở là một đại lượng vật lý biểu thị sự cản trở dòng điện trong một mạch điện. Điện trở được ký hiệu bằng chữ cái \(R\) và đơn vị đo là Ohm (\(\Omega\)). Trong một mạch điện, điện trở đóng vai trò quan trọng trong việc kiểm soát dòng điện, giúp bảo vệ các linh kiện điện tử khỏi bị quá tải và hư hỏng.
Theo định luật Ohm, điện trở của một đoạn mạch có thể được xác định bằng tỉ số giữa hiệu điện thế (\(U\)) đặt vào hai đầu đoạn mạch và cường độ dòng điện (\(I\)) chạy qua nó, được biểu diễn bởi công thức:
\[
R = \frac{U}{I}
\]
Trong đó:
- \(R\): Điện trở (\(\Omega\))
- \(U\): Hiệu điện thế (Vôn, \(V\))
- \(I\): Cường độ dòng điện (Ampe, \(A\))
Điện trở của một vật liệu không chỉ phụ thuộc vào các yếu tố như chiều dài, tiết diện ngang và điện trở suất của vật liệu mà còn có thể thay đổi theo nhiệt độ. Đối với một dây dẫn đồng chất, điện trở có thể tính toán dựa trên công thức:
\[
R = \frac{\rho \cdot L}{S}
\]
Trong đó:
- \(\rho\): Điện trở suất của vật liệu (\(\Omega \cdot m\))
- \(L\): Chiều dài của dây dẫn (m)
- \(S\): Tiết diện ngang của dây dẫn (m²)
Mỗi loại vật liệu có một điện trở suất khác nhau, làm cho khả năng dẫn điện của chúng cũng khác nhau. Chẳng hạn, đồng có điện trở suất thấp nên dẫn điện tốt, trong khi vật liệu như nhôm có điện trở suất cao hơn và do đó dẫn điện kém hơn.
Điện trở có vai trò quan trọng trong thiết kế và phân tích các mạch điện, đặc biệt là trong việc đảm bảo rằng các linh kiện trong mạch hoạt động ở mức an toàn và hiệu quả.
2. Công Thức Tính Điện Trở Toàn Phần
Trong mạch điện, điện trở toàn phần là điện trở tương đương của toàn bộ mạch khi các điện trở thành phần được kết nối theo một cách nhất định. Tùy thuộc vào cách các điện trở được mắc (nối tiếp hoặc song song), công thức tính điện trở toàn phần sẽ khác nhau. Dưới đây là hướng dẫn chi tiết từng bước để tính toán điện trở toàn phần trong các trường hợp khác nhau.
2.1. Công Thức Tính Điện Trở Toàn Phần Trong Mạch Nối Tiếp
Khi các điện trở được mắc nối tiếp, điện trở toàn phần là tổng của tất cả các điện trở thành phần:
\[
R_{tổng} = R_1 + R_2 + R_3 + \ldots + R_n
\]
Trong đó:
- \(R_{tổng}\): Điện trở toàn phần của mạch (\(\Omega\))
- \(R_1, R_2, R_3, \ldots, R_n\): Các điện trở thành phần trong mạch (\(\Omega\))
Ví dụ: Nếu có ba điện trở với giá trị lần lượt là \(5 \, \Omega\), \(10 \, \Omega\) và \(15 \, \Omega\) mắc nối tiếp, thì điện trở toàn phần sẽ là:
\[
R_{tổng} = 5 + 10 + 15 = 30 \, \Omega
\]
2.2. Công Thức Tính Điện Trở Toàn Phần Trong Mạch Song Song
Trong trường hợp các điện trở được mắc song song, điện trở toàn phần được tính bằng tổng nghịch đảo của tất cả các điện trở thành phần:
\[
\frac{1}{R_{tổng}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}
\]
Sau đó, lấy nghịch đảo của kết quả để tìm giá trị điện trở toàn phần:
\[
R_{tổng} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}}
\]
Ví dụ: Nếu có ba điện trở với giá trị lần lượt là \(4 \, \Omega\), \(6 \, \Omega\) và \(12 \, \Omega\) mắc song song, điện trở toàn phần sẽ là:
\[
\frac{1}{R_{tổng}} = \frac{1}{4} + \frac{1}{6} + \frac{1}{12} = \frac{3}{12} + \frac{2}{12} + \frac{1}{12} = \frac{6}{12} = 0.5 \, \Omega^{-1}
\]
Do đó, \(R_{tổng} = \frac{1}{0.5} = 2 \, \Omega\).
2.3. Công Thức Tính Điện Trở Toàn Phần Trong Mạch Kết Hợp
Trong các mạch phức tạp, nơi điện trở được mắc cả nối tiếp và song song, bạn cần phân chia mạch thành các phần nhỏ hơn và áp dụng các công thức trên cho từng phần. Sau khi tính toán các điện trở tương đương cho từng phần, bạn sẽ tiếp tục tính điện trở toàn phần của mạch.
Ví dụ, nếu bạn có một mạch gồm hai điện trở \(R_1 = 3 \, \Omega\) và \(R_2 = 6 \, \Omega\) mắc nối tiếp, và một điện trở khác \(R_3 = 2 \, \Omega\) mắc song song với tổ hợp nối tiếp này, điện trở toàn phần sẽ được tính như sau:
Đầu tiên, tính điện trở tương đương của \(R_1\) và \(R_2\):
\[
R_{12} = R_1 + R_2 = 3 + 6 = 9 \, \Omega
\]
Sau đó, tính điện trở toàn phần \(R_{tổng}\) khi kết hợp với \(R_3\):
\[
\frac{1}{R_{tổng}} = \frac{1}{R_{12}} + \frac{1}{R_3} = \frac{1}{9} + \frac{1}{2} = \frac{2}{18} + \frac{9}{18} = \frac{11}{18}
\]
Do đó, \(R_{tổng} = \frac{18}{11} \approx 1.64 \, \Omega\).
Bằng cách áp dụng các bước trên, bạn có thể dễ dàng tính toán điện trở toàn phần trong bất kỳ mạch điện nào, đảm bảo tính chính xác và hiệu quả trong thiết kế và phân tích mạch.

3. Ứng Dụng Của Điện Trở Trong Thực Tế
Điện trở là một thành phần quan trọng trong nhiều ứng dụng thực tế, từ các thiết bị điện tử đơn giản đến các hệ thống điện phức tạp. Dưới đây là một số ứng dụng tiêu biểu của điện trở trong đời sống hàng ngày và công nghiệp.
3.1. Điện Trở Trong Các Thiết Bị Điện Tử
Trong các mạch điện tử, điện trở được sử dụng để điều chỉnh dòng điện và điện áp nhằm bảo vệ các linh kiện như transistor, diode, và IC khỏi quá tải. Điện trở còn được sử dụng trong các mạch chia điện áp, mạch tạo xung và mạch lọc để đảm bảo hoạt động ổn định của thiết bị.
3.2. Ứng Dụng Trong Hệ Thống Chiếu Sáng
Điện trở được sử dụng trong các hệ thống chiếu sáng để hạn chế dòng điện qua bóng đèn, bảo vệ chúng khỏi bị cháy do dòng điện quá mức. Điều này đặc biệt quan trọng trong các loại đèn LED, nơi dòng điện phải được kiểm soát chặt chẽ để đảm bảo tuổi thọ của đèn.
3.3. Điện Trở Trong Hệ Thống Sưởi Và Điều Hòa
Trong các thiết bị sưởi như lò sưởi điện, bếp điện và máy nước nóng, điện trở được sử dụng để chuyển hóa năng lượng điện thành nhiệt năng. Các vật liệu có điện trở suất cao như Nichrome thường được sử dụng trong các dây nhiệt, giúp tạo ra nhiệt độ cao khi có dòng điện chạy qua.
3.4. Vai Trò Của Điện Trở Trong Điều Khiển Tốc Độ Động Cơ
Điện trở được sử dụng trong các bộ điều khiển tốc độ động cơ, giúp thay đổi tốc độ quay của động cơ bằng cách điều chỉnh mức điện áp và dòng điện cung cấp. Điều này rất quan trọng trong các ứng dụng như quạt, máy bơm, và các loại máy móc công nghiệp.
3.5. Ứng Dụng Trong An Toàn Điện
Điện trở cũng đóng vai trò quan trọng trong các mạch bảo vệ, chẳng hạn như mạch chống sét và mạch bảo vệ quá dòng. Chúng giúp hấp thụ và giảm bớt dòng điện đột ngột, bảo vệ các thiết bị và hệ thống điện khỏi hư hỏng.
Nhìn chung, điện trở là một thành phần không thể thiếu trong việc kiểm soát và điều chỉnh hoạt động của các thiết bị điện và điện tử, đóng góp lớn vào sự an toàn và hiệu quả của các hệ thống điện.

4. Hướng Dẫn Tính Toán Và Bài Tập Minh Họa
Trong phần này, chúng ta sẽ đi qua các bước cụ thể để tính toán điện trở toàn phần trong các mạch nối tiếp, song song và mạch kết hợp. Các ví dụ minh họa sẽ giúp bạn nắm vững phương pháp và áp dụng một cách chính xác trong thực tế.
4.1. Bài Tập Tính Điện Trở Toàn Phần Trong Mạch Nối Tiếp
Bài tập 1: Cho ba điện trở \(R_1 = 5 \, \Omega\), \(R_2 = 10 \, \Omega\), và \(R_3 = 15 \, \Omega\) mắc nối tiếp. Hãy tính điện trở toàn phần của mạch.
Giải:
Vì các điện trở được mắc nối tiếp, điện trở toàn phần \(R_{tổng}\) được tính bằng:
\[
R_{tổng} = R_1 + R_2 + R_3 = 5 + 10 + 15 = 30 \, \Omega
\]
Vậy điện trở toàn phần của mạch là \(30 \, \Omega\).
4.2. Bài Tập Tính Điện Trở Toàn Phần Trong Mạch Song Song
Bài tập 2: Cho ba điện trở \(R_1 = 6 \, \Omega\), \(R_2 = 12 \, \Omega\), và \(R_3 = 18 \, \Omega\) mắc song song. Hãy tính điện trở toàn phần của mạch.
Giải:
Trong trường hợp này, điện trở toàn phần \(R_{tổng}\) được tính bằng tổng nghịch đảo của các điện trở thành phần:
\[
\frac{1}{R_{tổng}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{6} + \frac{1}{12} + \frac{1}{18}
\]
Tính toán cụ thể:
\[
\frac{1}{R_{tổng}} = \frac{3}{18} + \frac{1.5}{18} + \frac{1}{18} = \frac{5.5}{18} = \frac{11}{36}
\]
Vậy điện trở toàn phần là:
\[
R_{tổng} = \frac{36}{11} \approx 3.27 \, \Omega
\]
4.3. Bài Tập Ứng Dụng Thực Tế
Bài tập 3: Cho mạch điện gồm hai điện trở \(R_1 = 4 \, \Omega\) và \(R_2 = 8 \, \Omega\) mắc nối tiếp, sau đó được mắc song song với điện trở \(R_3 = 6 \, \Omega\). Hãy tính điện trở toàn phần của mạch.
Giải:
Trước tiên, tính điện trở tương đương của \(R_1\) và \(R_2\) mắc nối tiếp:
\[
R_{12} = R_1 + R_2 = 4 + 8 = 12 \, \Omega
\]
Sau đó, tính điện trở toàn phần khi \(R_{12}\) mắc song song với \(R_3\):
\[
\frac{1}{R_{tổng}} = \frac{1}{R_{12}} + \frac{1}{R_3} = \frac{1}{12} + \frac{1}{6} = \frac{1}{12} + \frac{2}{12} = \frac{3}{12} = \frac{1}{4}
\]
Do đó, điện trở toàn phần của mạch là:
\[
R_{tổng} = 4 \, \Omega
\]
Bằng cách thực hiện các bước trên, bạn có thể dễ dàng tính toán điện trở toàn phần của bất kỳ mạch điện nào, từ đơn giản đến phức tạp, và đảm bảo sự chính xác trong thiết kế và kiểm tra các mạch điện trong thực tế.

5. Cách Đọc Giá Trị Điện Trở Từ Vòng Màu
Điện trở thường được mã hóa giá trị của nó thông qua các vòng màu được in trên thân điện trở. Việc hiểu rõ cách đọc giá trị từ các vòng màu này giúp bạn nhanh chóng xác định được điện trở của các linh kiện trong mạch điện. Dưới đây là hướng dẫn chi tiết cách đọc giá trị điện trở từ các vòng màu.
5.1. Số Vòng Màu Và Ý Nghĩa Của Chúng
Thông thường, điện trở có từ 4 đến 6 vòng màu, mỗi vòng đại diện cho một giá trị số hoặc hệ số nhân nhất định. Trong đó:
- Vòng 1: Chỉ số đầu tiên của giá trị điện trở.
- Vòng 2: Chỉ số thứ hai của giá trị điện trở.
- Vòng 3: Hệ số nhân (nhân với 10^x).
- Vòng 4: Sai số (tolerance) của điện trở, thường là ±1%, ±5%, hoặc ±10%.
- Vòng 5 và 6 (nếu có): Có thể đại diện cho các thông số khác như độ ổn định hoặc nhiệt độ.
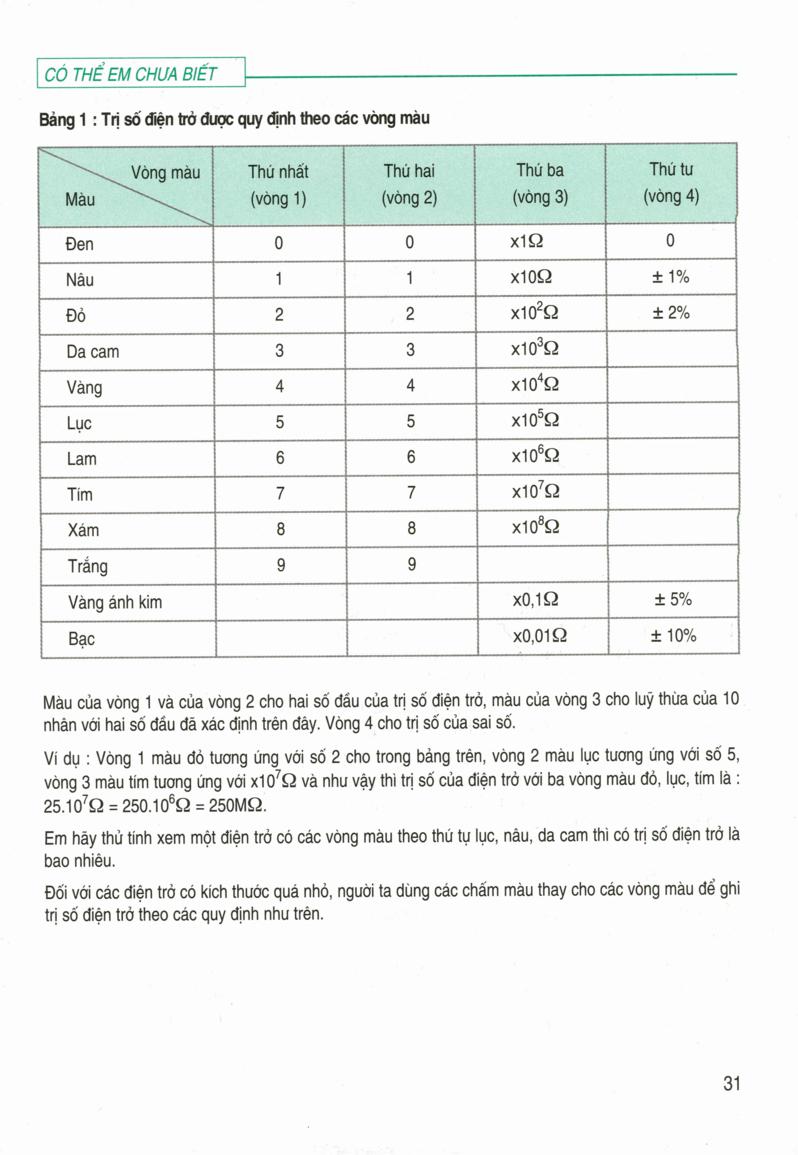
5.2. Bảng Màu Điện Trở
Dưới đây là bảng quy đổi giá trị của các vòng màu:
| Màu | Chữ Số | Hệ Số Nhân | Sai Số |
| Đen | 0 | \(10^0\) | N/A |
| Nâu | 1 | \(10^1\) | ±1% |
| Đỏ | 2 | \(10^2\) | ±2% |
| Cam | 3 | \(10^3\) | N/A |
| Vàng | 4 | \(10^4\) | N/A |
| Xanh Lục | 5 | \(10^5\) | ±0.5% |
| Xanh Dương | 6 | \(10^6\) | ±0.25% |
| Tím | 7 | \(10^7\) | ±0.1% |
| Xám | 8 | \(10^8\) | ±0.05% |
| Trắng | 9 | \(10^9\) | N/A |
| Vàng Kim | N/A | \(10^{-1}\) | ±5% |
| Bạc | N/A | \(10^{-2}\) | ±10% |
5.3. Ví Dụ Cụ Thể
Ví dụ: Một điện trở có các vòng màu theo thứ tự: Đỏ, Tím, Vàng, Vàng Kim. Hãy xác định giá trị của điện trở này.
Giải:
- Vòng 1: Đỏ = 2.
- Vòng 2: Tím = 7.
- Vòng 3: Vàng = \(10^4\).
- Vòng 4: Vàng Kim = ±5%.
Vậy giá trị của điện trở là:
\[
R = 27 \times 10^4 \, \Omega = 270,000 \, \Omega \, (\pm 5\%)
\]
Như vậy, điện trở có giá trị là 270kΩ với sai số ±5%.
XEM THÊM:
6. Kết Luận
Qua các phần đã trình bày, chúng ta có thể thấy rằng việc tính toán điện trở toàn phần và hiểu rõ về điện trở trong mạch điện là cực kỳ quan trọng trong cả lý thuyết lẫn ứng dụng thực tiễn. Các công thức và phương pháp tính toán được cung cấp không chỉ giúp bạn nắm vững nguyên lý cơ bản mà còn hỗ trợ trong việc phân tích và thiết kế các mạch điện phức tạp. Đồng thời, kỹ năng đọc giá trị điện trở từ vòng màu là cần thiết để xác định chính xác thông số của các linh kiện, đảm bảo hiệu quả và độ tin cậy trong các ứng dụng thực tế.
Bằng cách kết hợp các kiến thức này với các bài tập minh họa, bạn sẽ có được nền tảng vững chắc để tiếp cận và giải quyết các vấn đề liên quan đến điện trở và mạch điện một cách hiệu quả. Hãy tiếp tục thực hành và ứng dụng các kiến thức này vào thực tế để nâng cao kỹ năng và tự tin hơn trong lĩnh vực điện tử.








.jpg)