Khi ôn tập giữa kỳ 1 toán 12, chúng ta cần tổng hợp kiến thức đã học trong suốt kỳ 1 để lập kế hoạch ôn tập một cách bài bản. Tuy nhiên, việc này có thể gặp khó khăn nếu không biết ôn từ đâu và ôn cái gì trước. Để giúp bạn tổ chức ôn tập toán 12 giữa kỳ 1 một cách hiệu quả, bài viết này sẽ cung cấp cho bạn đề ôn tập, sơ đồ tư duy và đề cương chi tiết.
Contents
Các phần kiến thức ôn tập toán 12 kỳ 1 quan trọng
Trước khi bắt đầu ôn tập, hãy cùng nhau tìm hiểu những phần kiến thức quan trọng cần ôn tập toán 12 kỳ 1. Đây là những phần kiến thức mà chúng ta cần nắm vững để đạt được kết quả tốt trong kỳ thi giữa kỳ.
Bạn đang xem: Ôn tập giữa kì 1 toán 12: Full Đề – Sơ đồ tư duy – Đề cương
Ma trận đề ôn tập giữa kỳ 1 toán 12
Ma trận đề cương kiến thức ôn tập giữa kỳ 1 môn Toán
| Chủ đề | Nội dung |
|---|---|
| Nhận biết | Cực trị hàm bậc 3, sự biến thiên của hàm bậc 3, tiệm của hàm số bậc 1/bậc 1, đồ thị, y, y’ ,… |
| Thông hiểu | Chọn hàm số bậc 3, bậc 1/bậc 1, đồng biến/ nghịch biến trên tập xác định của hàm số cho trước |
| Vận dụng thấp | Xác định m để hàm số đồng biến/ nghịch biến trên tập xác định (khoảng cho trước) Cực trị |
| Nhận biết | Xác định điểm cực trị của hàm số y = f(x); xác định điểm cực đại và cực tiểu của hàm số y = f(x) |
| Thông hiểu | Xác định m để hàm số bậc 3 có cực đại, cực tiểu |
| Vận dụng thấp | Xác định m để hàm số y = f(x) đạt cực trị thỏa mãn điều kiện cho trước, xác định cực trị của hàm bậc 4 trùng phương |
| Vận dụng cao | Cực trị hàm trị tuyệt đối (có tham số hoặc không có tham số) Giá trị lớn nhất – Giá trị nhỏ nhất |
| Nhận biết | Tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [a; b], (a; b) |
| Thông hiểu | Dựa trên đồ thị xác định GTLN – GTNN; xác định GTLN – GTNN của hàm số y = (ax² + bx + c)/(dx + e) |
| Vận dụng thấp | Tìm GTLN – GTNN của hàm số chứa căn hoặc trị tuyệt đối |
| Vận dụng cao | Bài toán thực tế Tiệm cận: Tiệm cận ngang Tiệm cận đứng |
| Nhận biết | Xác định tiệm cận của hàm số dạng bậc 1/bậc 1 |
| Thông hiểu | Số tiệm cận của đồ thị hàm số y = (ax² + bx + c)/(dx² + ex + f) |
| Vận dụng thấp | Xác định m để hàm số có số tiệm cận theo yêu cầu, xác định m để đường tiệm cận của đồ thị qua điểm cho trước. Đồ thị |
| Thông hiểu | Xác định đồ thị dạng y = f(x) |
| Thông hiểu | Xác định hàm số có đồ thị bậc 4, trùng phương cho trước |
| Thông hiểu | Xác định hàm số có đồ thị bậc 1/bậc 1 |
| Sự tương giao | Xác định số giao điểm của 2 đồ thị, biện luận theo m số nghiệm của phương trình |
| Vận dụng thấp | Xác định giao điểm của 2 đồ thị và thực hiện các phép tính đơn giản. Xác định khoảng cách của 2 giao điểm của 2 đồ thị |
| Bài toán thực tế | Ứng dụng GTLN – GTNN, cực trị để giải quyết bài toán thực tế |
| Khái niệm, phân loại khối đa diện | Công thức thể tích hình chóp, phân loại đa diện đều, gọi tên đa diện đều, xác định khối đa diện lồi, tính chất đối xứng của khối đa diện |
| Thông hiểu | Khái niệm hình hộp, khái niệm hình hộp chữ nhất, các mặt/ cạnh của khối đa diện, tỉ số thể tích Thể tích khối đa diện, tỉ số thể tích khối đa diện |
| Nhận biết | Công thức thể tích chóp / lăng trụ |
| Thông hiểu | Tính thể tích khối chóp có đường cao vuông góc với đáy/lăng trụ đứng |
| Vận dụng thấp | Tính thể tích hình chóp chưa có sẵn đường cao (cho trước góc, mặt bên vuông đáy,…) |
| Vận dụng thấp | Tỉ số thể tích hình chóp |
| Vận dụng cao | Tính tỉ số độ dài dựa vào tỉ số thể tích của 2 khối chóp được tạo thành bởi 1 mặt phẳng qua 1 đỉnh và song song đt của khối đa diện,… |
Sơ đồ tư duy ôn tập giữa kỳ 1 toán 12
Khi ôn đề thi giữa học kỳ 1 lớp 12 môn toán, nhiều bạn sẽ gặp khó khăn không biết ôn từ đâu và ôn cái nào trước, cũng như khó nhớ các kiến thức đã học. Để giải quyết vấn đề này, chúng ta có thể sử dụng sơ đồ tư duy. Sơ đồ tư duy sẽ giúp chúng ta tổng hợp các lý thuyết và công thức một cách dễ nhìn và dễ nhớ. Dưới đây là một số sơ đồ tư duy về cực trị hàm số trong đề thi giữa học kỳ 1 lớp 12 môn toán:
Sơ đồ tư duy phần đại số
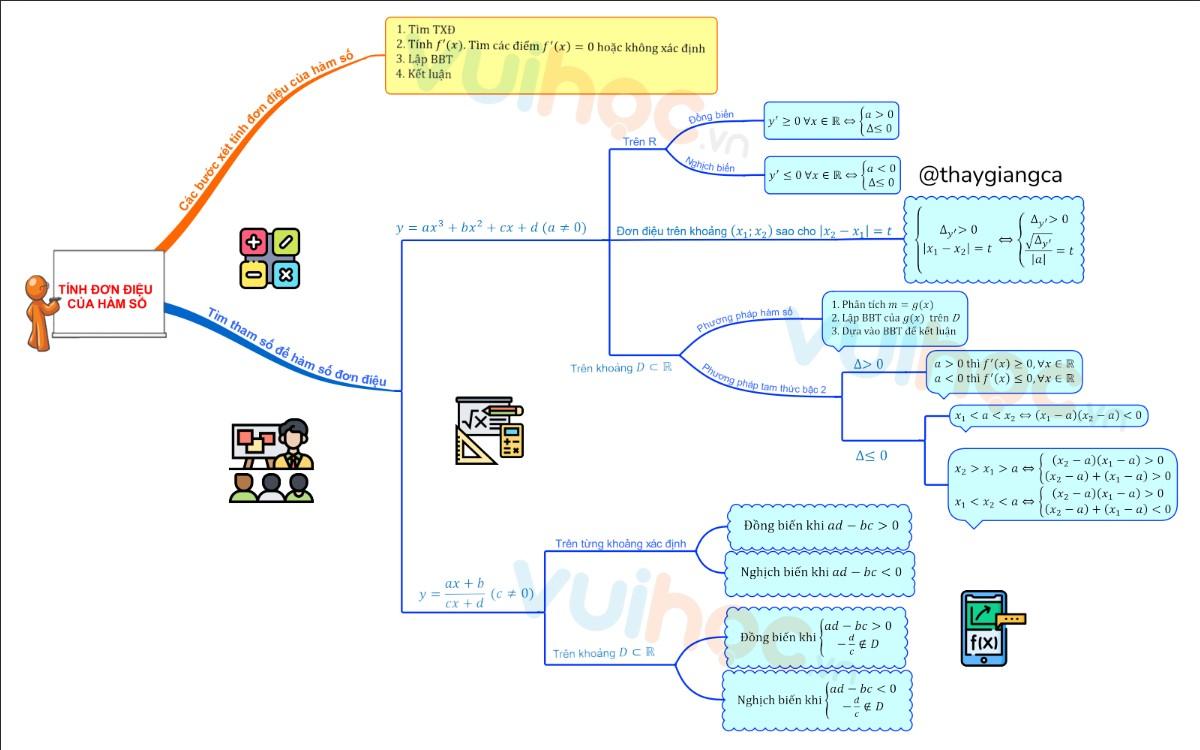
Sơ đồ tư duy tính đơn điệu hàm số
Sơ đồ tư duy cực trị hàm số
Sơ đồ tư duy giá trị lớn nhất, giá trị nhỏ nhất của hàm số
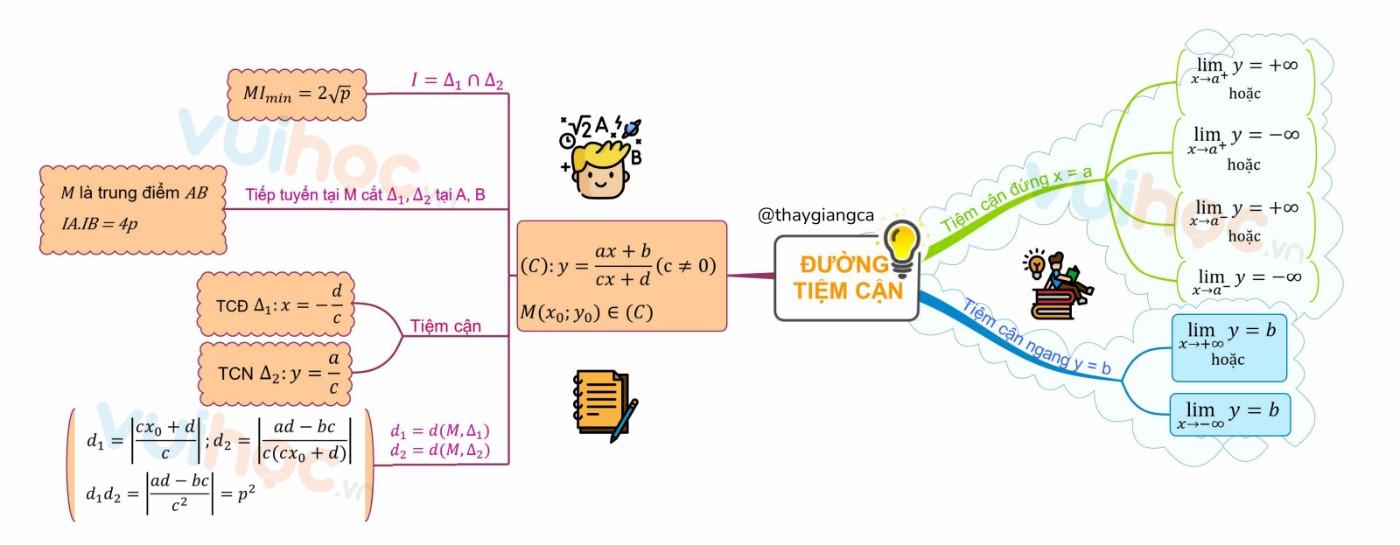
Sơ đồ tư duy đường tiệm cận
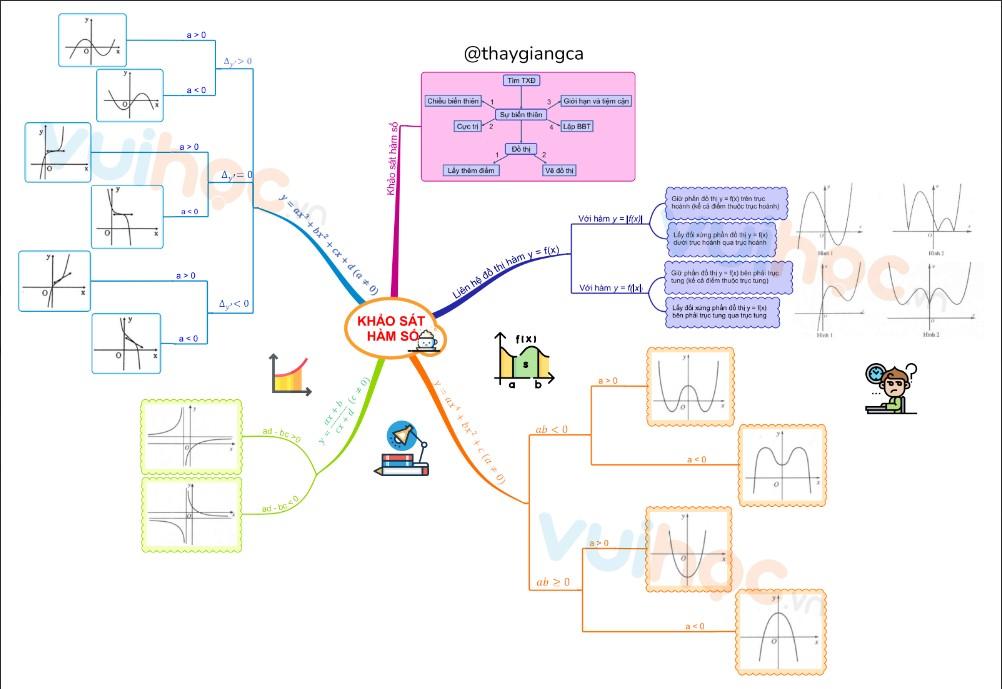
Sơ đồ tư duy khảo sát hàm số
Xem thêm : Từ điển phương trình hóa học | Marathon Education
Sơ đồ tư duy phần hình học
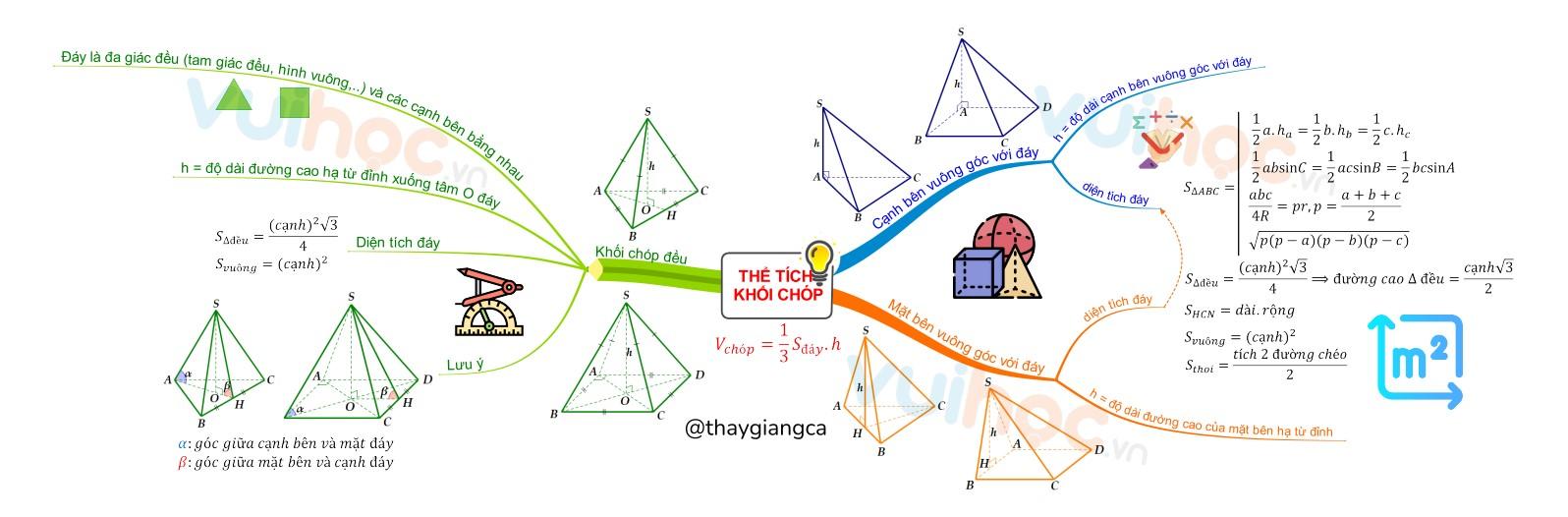
Sơ đồ tư duy thể tích hình chóp
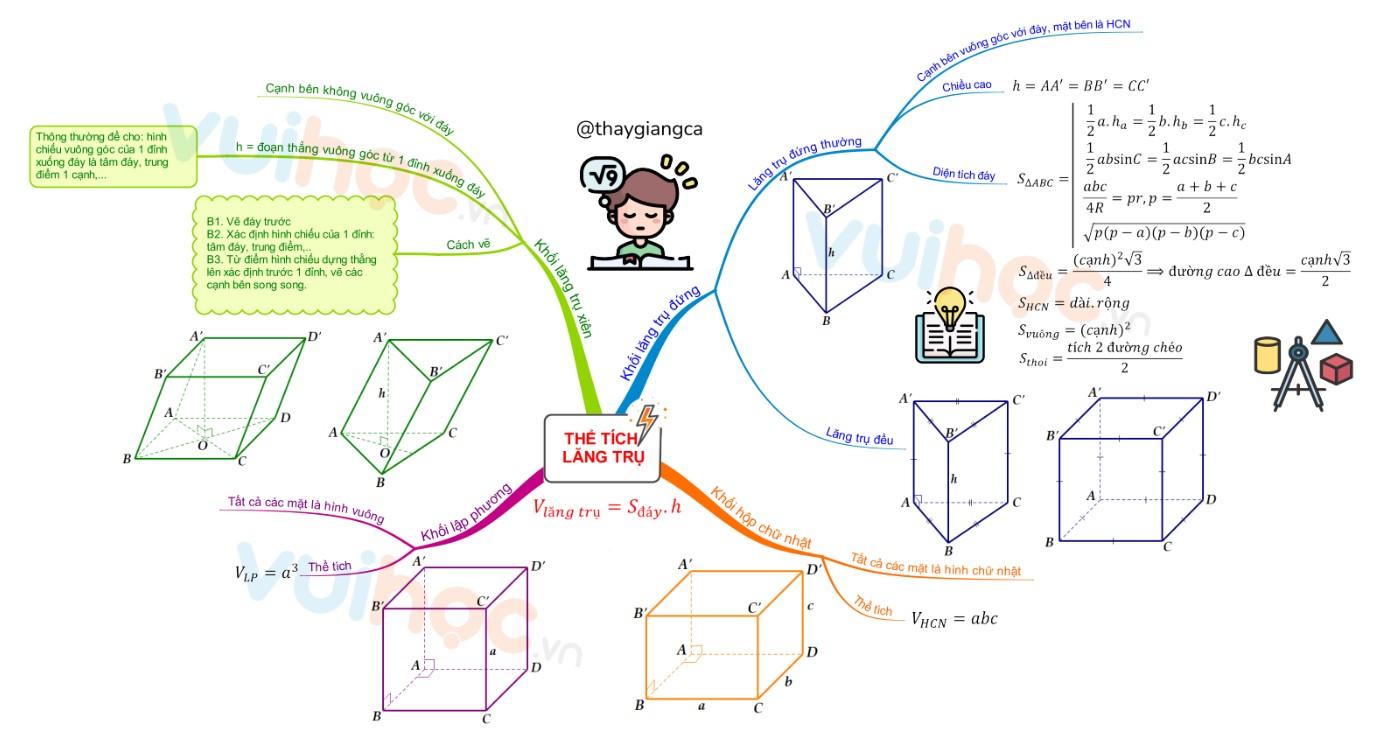
Sơ đồ tư duy thể tích hình lăng trụ
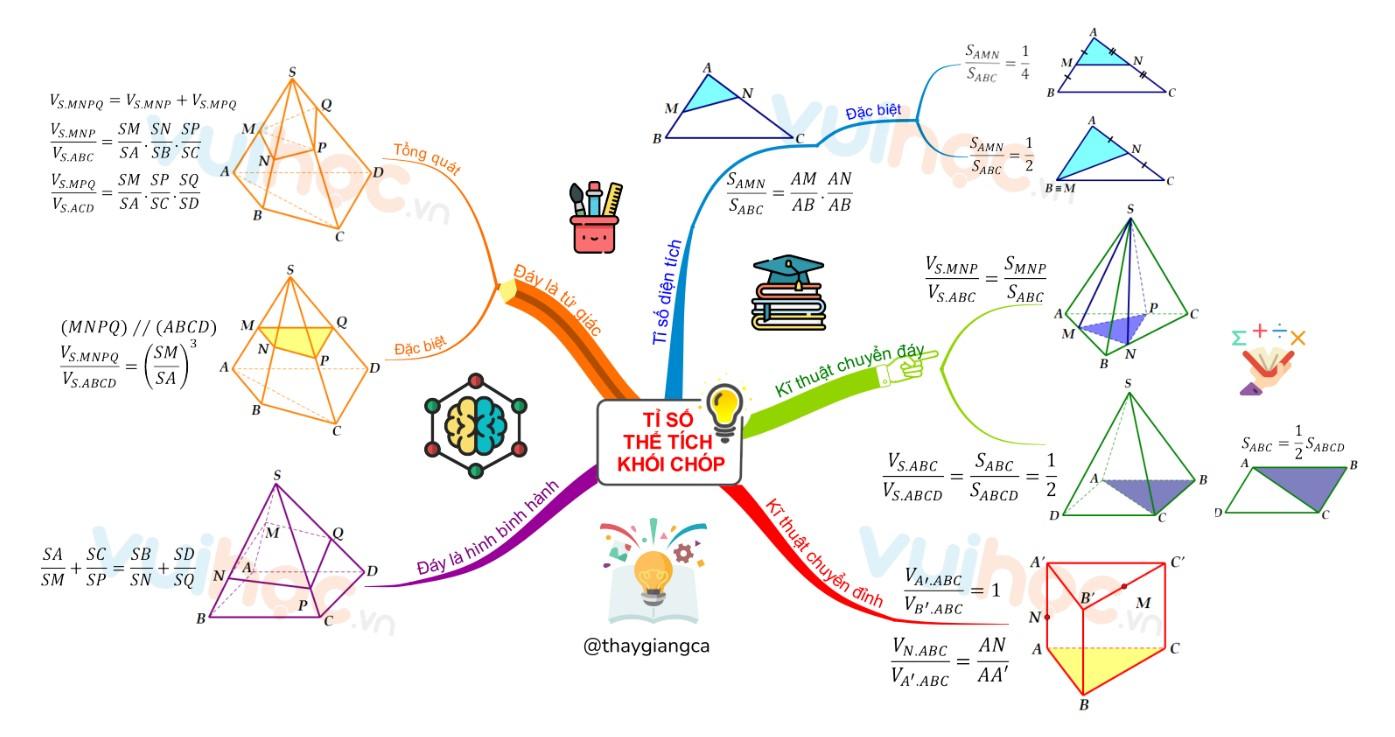
Sơ đồ tư duy tỉ lệ thể tích hình chóp
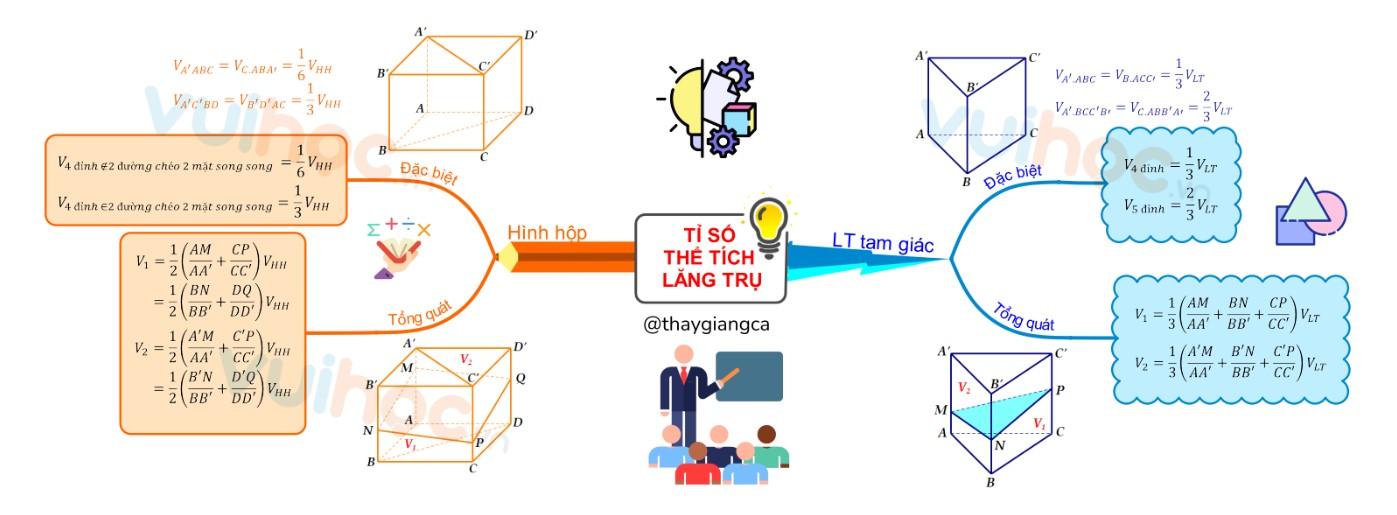
Sơ đồ tư duy tỉ lệ thể tích hình lăng trụ
Cuối cùng, để đạt kết quả tốt nhất trong kỳ thi giữa kỳ, chúng ta phải luyện tập thật nhiều đề thi. Để giúp bạn, đã có bộ đề ôn tập giữa kỳ 1 toán 12 được biên soạn bởi các thầy cô chuyên môn của VUIHOC. Bạn có thể tải về ngay để luyện tập:
Chúc bạn ôn tập hiệu quả và đạt được kết quả tốt trong kỳ thi giữa kỳ 1 toán 12!
Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tư duy
.png)