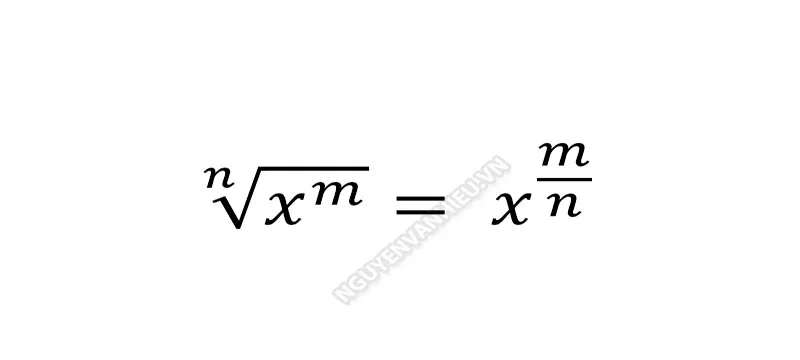Giới thiệu
Bạn đang tìm hiểu về phương pháp giải hệ phương trình tuyến tính? Trong bài viết này, chúng tôi sẽ giới thiệu đến bạn phương pháp giải hệ PTTT (Phương Trình Tuyến Tính) bằng phương pháp trụ xoay của Gauss – một phương pháp đơn giản và hiệu quả.
.png)
Phương pháp trụ xoay của Gauss
Phương pháp trụ xoay của Gauss là một cách tiếp cận thông minh để giải hệ PTTT. Đầu tiên, chúng ta xây dựng ma trận đầy đủ của hệ. Ngược lại, cho một ma trận đầy đủ bất kỳ, chúng ta cũng có thể xây dựng lại được hệ phương trình tương ứng với ma trận đó.
Bạn đang xem: 3.3. Giải hệ PTTT bằng phương pháp Gauss
Xem thêm : Hình ảnh đẹp chúc mừng mùng 1 đầu tháng, mang theo may mắn và bình an
Nếu ma trận đầy đủ có dạng đặc biệt như tam giác trên hoặc hình thang, việc giải hệ phương trình tương ứng sẽ trở nên đơn giản hơn nhiều (suy từ dưới lên).
Các phép biến đổi sơ cấp
Phương pháp trụ xoay của Gauss cho phép chúng ta thực hiện các phép biến đổi sơ cấp trên ma trận đầy đủ. Điều này đồng nghĩa với việc chúng ta cũng thực hiện các phép biến đổi tương ứng trên hệ phương trình.
Đối với ma trận $bar{A}$, chúng ta có thể nhân một hàng với một số $kneq$0, đổi chỗ hai hàng, hoặc cộng bội của một hàng vào một hàng khác mà không làm thay đổi tập nghiệm của hệ phương trình.
Xem thêm : Lịch nghỉ hè năm 2024 của học sinh 63 tỉnh thành (Dự kiến)
Việc sử dụng các phép biến đổi sơ cấp (về hàng) trên ma trận $bar{A}$ cũng chính là thực hiện các phép biến đổi sơ cấp đối với hệ phương trình tương ứng. Đưa $bar{A}$ về dạng bậc thang đồng nghĩa với việc biến đổi hệ phương trình ban đầu thành một hệ tương đương đơn giản hơn, từ đó chúng ta dễ dàng suy ra nghiệm.

Kết luận
Trong bài viết này, chúng tôi đã giới thiệu đến bạn phương pháp giải hệ PTTT bằng phương pháp trụ xoay của Gauss. Đây là một phương pháp đơn giản, nhưng rất hiệu quả và tiện lợi cho việc giải quyết các bài toán liên quan đến hệ phương trình tuyến tính.
Hy vọng rằng bạn đã có được những thông tin hữu ích và có thể áp dụng phương pháp này trong công việc và học tập của mình. Hãy tiếp tục theo dõi các bài viết tiếp theo để khám phá thêm nhiều kiến thức bổ ích khác.
Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập