RÈN LUYỆN NĂNG LỰC PHÁT HIỆN VÀ GIẢI QUYẾT VẤN ĐỀ CHO HỌC SINH TIỂU HỌC THÔNG QUA DẠY HỌC MÔN TOÁN

Tác giả: PGS. TS. Chu Cẩm Thơ, Nhà sáng lập, Giám đốc nghiên cứu và đào tạo POMATH

Năng lực giải quyết vấn đề (GQVĐ) đóng vai trò quan trọng trong việc phát triển con người, và nhiều nền giáo dục tiên tiến trên thế giới đang nhấn mạnh sự phát triển năng lực này. Tuy nhiên, ở Việt Nam, việc học quá chú trọng vào kỹ năng và luyện tập theo mô hình có sẵn khiến cho học sinh (HS) không được rèn luyện năng lực GQVĐ từ sớm. Điều này ảnh hưởng không nhỏ đến năng lực tự học, tự khám phá và tư duy của trẻ. Vì vậy, việc rèn luyện HS phát hiện, đặt ra và giải quyết vấn đề trong học tập, cuộc sống cá nhân, gia đình và cộng đồng không chỉ có ý nghĩa trong phương pháp dạy học mà còn là mục tiêu quan trọng trong giáo dục và đào tạo.

Bạn đang xem: RÈN LUYỆN NĂNG LỰC PHÁT HIỆN VÀ GIẢI QUYẾT VẤN ĐỀ CHO HỌC SINH TIỂU HỌC THÔNG QUA DẠY HỌC MÔN TOÁN

Rèn luyện năng lực phát hiện và giải quyết vấn đề cho HS tiểu học thông qua một số nội dung dạy học

Theo quan điểm triết học duy vật biện chứng, mâu thuẫn luôn là động lực của sự phát triển. Tình huống có vấn đề là một biểu hiện hợp lý của quan hệ bên trong giữa tri thức, kinh nghiệm và kỹ năng đã có với yêu cầu giải thích các sự kiện mới hoặc mang tính đột phá. Theo Rubinstein, một tình huống có vấn đề là nguồn gốc của sự sáng tạo và tư duy sáng tạo.

Trong dạy học, một vấn đề thường được hiểu là một bài toán chưa có lời giải. Tuy nhiên, vấn đề cũng mang trong mình tiềm năng để giải quyết đối với học sinh. Trong phạm vi bài viết này, chúng tôi muốn tập trung vào khía cạnh “giải quyết vấn đề” như một năng lực cần phát triển cho HS và liên kết nội dung dạy học.

Trong môn Toán ở tiểu học, “giải quyết vấn đề” liên quan đến các bài toán có lời văn, các bài toán logic – tổ hợp, các bài toán thực tế… Khi gặp các bài toán này, học sinh cần có khả năng phân tích và chuyển đổi bài toán thành dạng toán quen thuộc. Dưới đây là sơ đồ mô tả quá trình tìm kiếm hướng giải quyết bài toán:

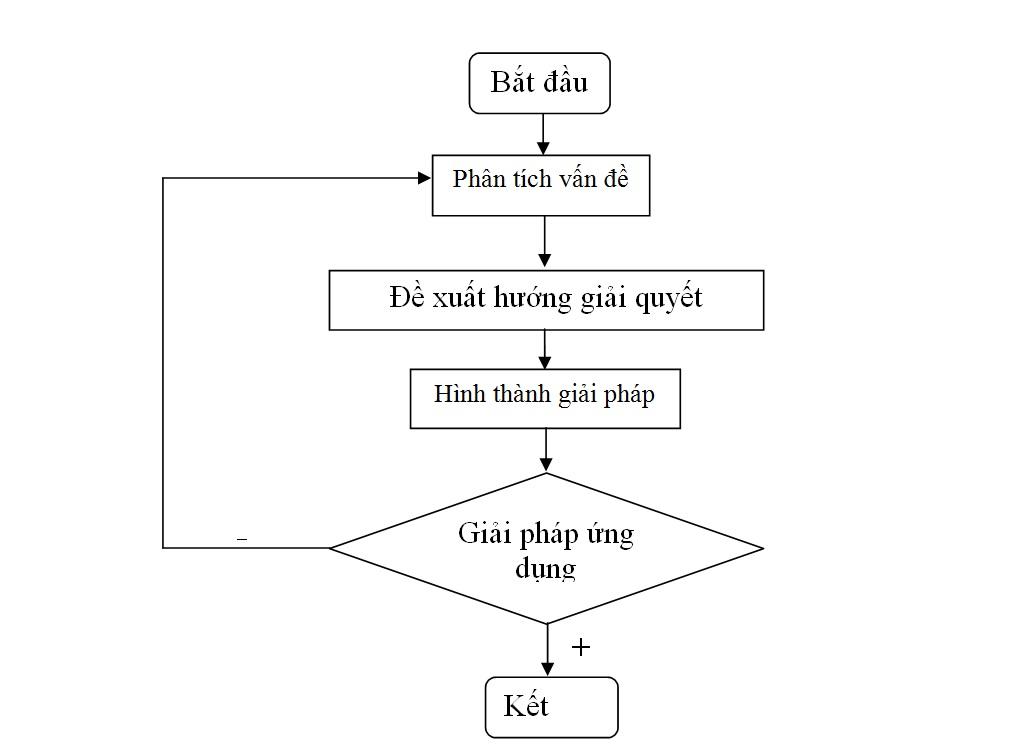
Hình 1: Sơ đồ tìm hướng giải quyết bài toán.

Đối với trẻ mới làm quen với các bài toán “giải quyết vấn đề”, đây thực sự là một thách thức. Trẻ cần được hướng dẫn và giải thích từng bước. Điều quan trọng là giúp trẻ hiểu bản chất của vấn đề và quan hệ giữa các yếu tố trong bài toán. Đồng thời, trẻ cũng cần được giúp đỡ để hiểu các mối quan hệ, kỹ năng sống trong cuộc sống thông qua các bài toán.

Giảng giải cho trẻ cần giúp trẻ hiểu rõ kiến thức toán học và áp dụng vào bài toán. Một số ví dụ cụ thể để minh họa điều này:

Ví dụ 1 (với HS 5 – 6 tuổi): Chọn giày hoặc dép phù hợp cho mỗi nhân vật trong tranh và ghép:

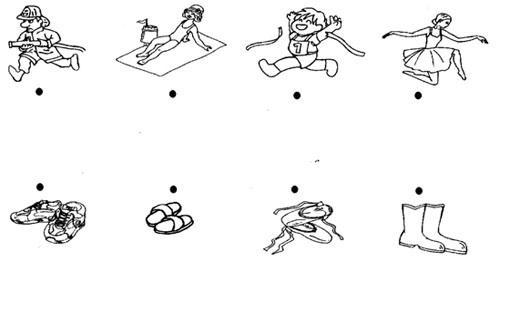
Hình 2: Ví dụ 1

Với dạng bài tập này, HS được rèn luyện năng lực thu thập thông tin (hiểu biểu tượng), suy luận các mối liên hệ và giải quyết bài toán thông qua các bước:

Xem thêm : Gợi ý 10 cách dạy toán cho trẻ chuẩn bị vào lớp 1 giúp con học toán vui, bố mẹ bớt lo lắng

Bước 1: Quan sát, nhận dạng hình ảnh trong tranh. Hàng trên lần lượt là: lính cứu hỏa, cô gái đi biển, vận động viên thể thao, cô gái múa ba lê. Hàng dưới bao gồm: đôi giày thể thao, dép tông, giày vải mềm và ủng cao su.

Bước 2: Phân tích, tìm hướng giải quyết.

Ở đây, hướng giải quyết chủ yếu là sử dụng phương pháp thử chọn và loại trừ, một phương pháp rất hữu ích trong việc giải các bài toán trắc nghiệm và có thể áp dụng trong nhiều tình huống thực tế. Ví dụ: Lính cứu hỏa không nên đi giày thể thao hay giày vải vì dễ bị ướt, và không nên đi dép tông vì không thể chạy nhanh và trơn. Lính cứu hỏa nên đi ủng, vì đó là sự lựa chọn tốt nhất. Các bước tiếp theo sẽ tương tự.

Ví dụ 2 (HS 6-7 tuổi): Đặt đề toán cho hình vẽ sau và giải chúng.

Hình vẽ có thể đặt được nhiều đề bài khác nhau, tùy vào khả năng ngôn ngữ và trí tưởng tượng của các em.

Ví dụ 3 (HS 7 – 8 tuổi): Hai chị em chia nhau 5 cái kẹo. Biết em ăn nhiều hơn chị 1 cái. Hỏi mỗi chị em ăn mấy cái kẹo?

Với các ví dụ trên, các giải pháp tìm được có thể được sắp xếp như sau:

a) Nếu đi trong phạm vi 200 km, có thể chọn xe của công ty C.

b) Nếu đi trong phạm vi 400 km, có thể chọn xe của công ty B.

Xem thêm : CÁCH DỖ TRẺ KHÔNG CHỊU ĐI HỌC

c) Nếu đi trong phạm vi 600 km, chọn xe của công ty A.

Ví dụ 5 (HS 10-11 tuổi): Trong một đêm tối cả gia đình gồm 5 người đi đến một chiếc cầu hẹp và không có lan can bảo vệ. Gia đình chỉ có một chiếc đèn pin. Mỗi người qua cầu mất thời gian khác nhau. Làm sao để gia đình có thể qua cầu trong thời gian 30 phút?

Câu trả lời cho ví dụ này là các thành viên gia đình cần tổ chức việc qua cầu theo các bước như sau:

Lượt 1: A và B đi, A về. Tổng thời gian: 4 phút.

Lượt 2: D và E đi, B về. Tổng thời gian: 15 phút.

Lượt 3: A và C đi, A về. Tổng thời gian: 7 phút.

Lượt 4: A và B đi. Tổng thời gian: 3 phút.

Tổng thời gian cả gia đình mất là 29 phút.

Kết luận: Năng lực giải quyết vấn đề là một trong những năng lực quan trọng của con người, và việc rèn luyện năng lực này cho HS tiểu học thông qua môn Toán rất cần thiết. Cần chú trọng vào các bài toán có vấn đề để học sinh rèn luyện và phát triển năng lực phát hiện và giải quyết vấn đề.

Tài liệu tham khảo:

1. Dương Thu Mai (2012), Đổi mới đánh giá giáo dục theo hướng đánh giá năng lực của học sinh.
2. Lương Việt Thái (2011), Phát triển năng lực giải quyết vấn đề thực tiễn của học sinh qua dạy học khoa học ở tiểu học.
3. Chu Cẩm Thơ (2012), Chương trình dạy Toán hướng cá nhân dành cho trẻ em – POMATH.

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tư duy