Bài 1: Hệ phương trình tuyến tính

Hệ phương trình tuyến tính là một đề tài quan trọng trong học đại số. Trong bài viết này, chúng ta sẽ tìm hiểu về hệ phương trình tuyến tính và cách giải chúng.

Giới thiệu

Hệ phương trình tuyến tính là một tập hợp các phương trình tuyến tính có cùng biến số x. Mục tiêu của chúng ta là tìm ra các giá trị của x sao cho các phương trình trong hệ đồng thời được thỏa mãn.

Bạn đang xem: Bài 1: Hệ phương trình tuyến tính

Ví dụ

Ví dụ sau đây sẽ giúp chúng ta hiểu rõ hơn về hệ phương trình tuyến tính:

2x₁ - x₂ + x₃ - 3x₄ = 1
x₁ - 4x₃ + 5x₄ = -2
-2x₂ + x₄ = 0

Xem thêm : Con chuột tiếng Anh là gì: Định nghĩa, ví dụ Anh Việt

Đặt A là ma trận hệ số, X là vectơ ẩn, và B là vectơ bên phải của hệ. Khi đó, hệ phương trình trên có thể viết lại dưới dạng ma trận là AX = B.

A = [[2, -1, 1, -3],
     [1, 0, -4, 5],
     [0, -2, 0, 1]]

X = [x₁, x₂, x₃, x₄]

B = [1, -2, 0]

Phương pháp giải

Một phương pháp thông dụng để giải hệ phương trình tuyến tính là phương pháp Gauss, đưa ma trận hệ số về dạng bậc thang hay bậc thang thu gọn bằng các phép biến đổi sơ cấp trên dòng.

Ví dụ: Giải hệ phương trình tuyến tính sau đây:

x₁ - 2x₂ - x₃ = -6
2x₁ - x₂ + x₃ = 3
x₁ + x₃ = 4

Ta có ma trận hệ số mở rộng của hệ là:

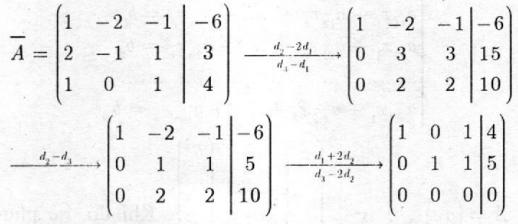
Hệ này tương đương với:

x₁ + x₃ = 4
x₂ + x₃ = 5

Vậy nghiệm của hệ là x₁ = 4 – x₃, x₂ = 5 – x₃, với x₃ là một số thực. Như vậy, hệ phương trình có vô số nghiệm với nghiệm tổng quát là X = (4 – x₃, 5 – x₃, x₃).

Kết luận

Hệ phương trình tuyến tính là một chủ đề quan trọng trong học đại số. Chúng ta đã tìm hiểu về khái niệm, ví dụ và phương pháp giải hệ phương trình tuyến tính. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về chủ đề này.

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập