Chủ đề ví dụ về lực đàn hồi: Bài viết này sẽ đưa bạn đến với những ví dụ chi tiết về lực đàn hồi trong đời sống, từ lò xo đến các ứng dụng kỹ thuật. Hiểu rõ hơn về định luật Hooke và cách lực đàn hồi tác động lên vật liệu sẽ giúp bạn áp dụng vào thực tế một cách hiệu quả nhất.
Mục lục
Lực Đàn Hồi và Các Ví Dụ Minh Họa
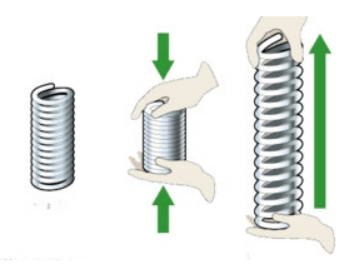
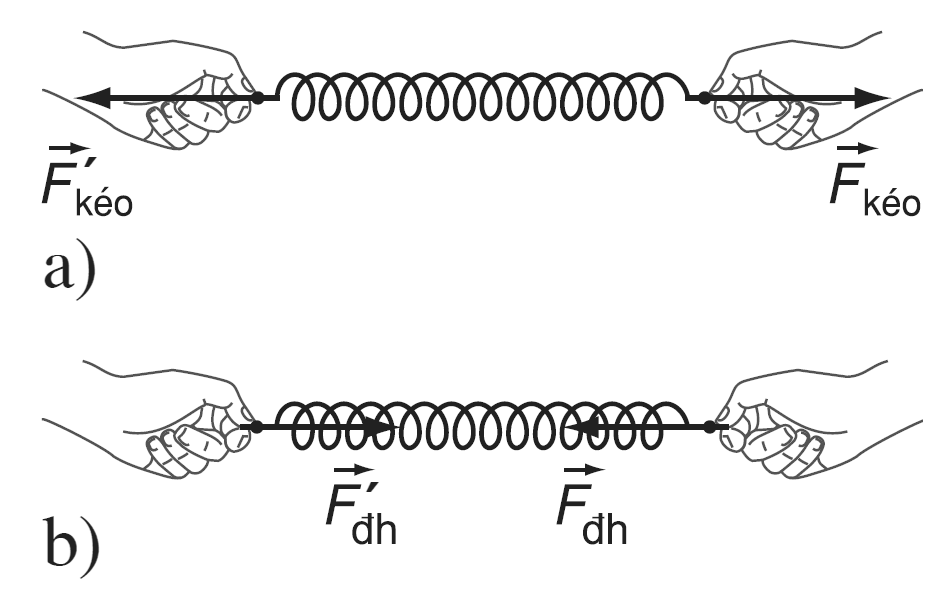
Lực đàn hồi là lực xuất hiện khi một vật bị biến dạng đàn hồi, có xu hướng chống lại nguyên nhân gây ra biến dạng. Đây là một khái niệm quan trọng trong vật lý học, đặc biệt liên quan đến các định luật về lực và chuyển động.
1. Định Luật Húc (Hooke)
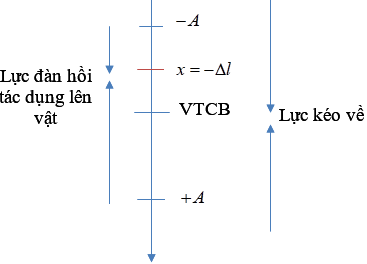
Trong giới hạn đàn hồi, lực đàn hồi của một vật tỉ lệ thuận với độ biến dạng của nó. Công thức định luật Húc được biểu diễn như sau:
$$F_{đh} = k \cdot |\Delta \ell|$$
- Trong đó:
- Fđh: Lực đàn hồi (N)
- k: Hệ số đàn hồi hoặc độ cứng của lò xo (N/m)
- Δℓ: Độ biến dạng của lò xo (m)
2. Ví Dụ Về Lực Đàn Hồi
- Ví dụ 1: Một lò xo có chiều dài tự nhiên là 10 cm và độ cứng là 40 N/m. Khi tác dụng vào đầu kia một lực 1 N để nén lò xo, chiều dài của lò xo khi bị nén là bao nhiêu?
- Ví dụ 2: Một lò xo có chiều dài tự nhiên là 30 cm, khi bị nén lò xo dài 24 cm và lực đàn hồi của nó bằng 5 N. Hỏi khi lực đàn hồi bị nén bằng 10N thì chiều dài của nó là bao nhiêu?
Hướng dẫn: Sử dụng công thức định luật Húc để tính toán.
Hướng dẫn: Tương tự, sử dụng công thức định luật Húc để giải quyết.
3. Ứng Dụng Của Lực Đàn Hồi
Lực đàn hồi có nhiều ứng dụng trong đời sống và kỹ thuật, chẳng hạn như trong các hệ thống giảm chấn, xây dựng cầu treo, và các thiết bị cơ khí khác. Một ví dụ điển hình là:
- Cầu treo: Lực căng của dây cáp treo giúp giữ thăng bằng cho cầu, đảm bảo cầu hoạt động ổn định dưới các điều kiện tải trọng khác nhau.
4. Các Bài Tập Thực Hành
| Bài 1: | Khi nói về lực đàn hồi của lò xo, phát biểu nào sau đây là đúng? |
| A. | Lực đàn hồi luôn có chiều ngược với chiều biến dạng của lò xo. |
| B. | Trong giới hạn đàn hồi, lực đàn hồi luôn tỉ lệ thuận với độ biến dạng. |
| C. | Khi lò xo bị dãn, lực đàn hồi có phương dọc theo trục lò xo. |
| D. | Lò xo luôn lấy lại được hình dạng ban đầu khi thôi tác dụng lực. |

.png)
Lực Đàn Hồi Là Gì?
Lực đàn hồi là lực xuất hiện khi một vật liệu bị biến dạng nhưng có khả năng quay trở lại trạng thái ban đầu. Đây là lực tự nhiên của các vật liệu như lò xo, dây cao su, hay bất kỳ vật thể nào có tính đàn hồi. Định luật Hooke là cơ sở để giải thích lực đàn hồi trong các vật liệu này.
- Định luật Hooke: Định luật này mô tả mối quan hệ giữa lực đàn hồi và độ biến dạng của vật liệu. Công thức toán học cho định luật này là \( F = -k \cdot \Delta x \), trong đó \( F \) là lực đàn hồi, \( k \) là hằng số đàn hồi, và \( \Delta x \) là độ biến dạng.
- Ứng dụng: Lực đàn hồi được ứng dụng rộng rãi trong kỹ thuật, xây dựng, và đời sống hàng ngày. Ví dụ điển hình là lò xo trong các hệ thống giảm xóc, dây thun, và các thiết bị tập thể dục.
Để tính toán lực đàn hồi, ta cần xác định được các thông số như hằng số đàn hồi \( k \) và độ biến dạng \( \Delta x \). Những thông số này giúp dự đoán và điều chỉnh các hệ thống hoạt động dựa trên nguyên tắc đàn hồi.
Các Ví Dụ Về Lực Đàn Hồi
Lực đàn hồi có thể được thấy trong nhiều tình huống hàng ngày và trong các ứng dụng kỹ thuật khác nhau. Dưới đây là một số ví dụ tiêu biểu:
- Lực đàn hồi của lò xo: Khi bạn kéo giãn hoặc nén lò xo, lực đàn hồi xuất hiện để đưa lò xo trở về chiều dài ban đầu. Độ lớn của lực này tuân theo định luật Hooke với công thức \( F = -k \cdot \Delta x \), trong đó \( k \) là hằng số đàn hồi của lò xo, và \( \Delta x \) là độ biến dạng.
- Lực đàn hồi trong dây cao su: Khi kéo giãn dây cao su, nó cũng sinh ra một lực đàn hồi để chống lại sự kéo giãn đó. Đặc điểm này được áp dụng trong nhiều sản phẩm như dây buộc, dây thun trong quần áo, hoặc dây tập thể dục.
- Lực đàn hồi trong cấu trúc cầu: Các cầu thép và cầu treo sử dụng đặc tính đàn hồi của các dây cáp thép để chịu tải trọng và giúp cầu duy trì hình dạng khi chịu lực tác động từ phương tiện giao thông và gió.
- Lực đàn hồi của bề mặt tiếp xúc: Khi đặt một vật nặng lên mặt phẳng, như một quả bóng đặt trên mặt bàn, mặt bàn sẽ sinh ra lực đàn hồi ngược lại để hỗ trợ quả bóng, đảm bảo nó không chìm xuống.
Những ví dụ trên cho thấy lực đàn hồi đóng vai trò quan trọng trong cả đời sống hàng ngày lẫn các ứng dụng công nghiệp. Việc hiểu rõ lực đàn hồi và các yếu tố liên quan giúp chúng ta thiết kế và sử dụng vật liệu một cách hiệu quả và an toàn hơn.

Các Công Thức Tính Lực Đàn Hồi
Để tính toán lực đàn hồi trong các vật thể như lò xo, dây cao su, hoặc các vật liệu đàn hồi khác, có một số công thức cơ bản được sử dụng. Dưới đây là các công thức chính giúp bạn tính toán lực đàn hồi một cách chính xác:
- Công thức Định luật Hooke: Đây là công thức cơ bản nhất để tính lực đàn hồi trong một lò xo:
\[
F = -k \cdot \Delta x
\]
Trong đó:
- \( F \): Lực đàn hồi (đơn vị: Newton, N)
- \( k \): Hằng số đàn hồi của lò xo (đơn vị: N/m)
- \( \Delta x \): Độ biến dạng của lò xo (đơn vị: mét, m)
- Công thức năng lượng đàn hồi: Năng lượng đàn hồi lưu trữ trong một lò xo bị nén hoặc kéo giãn được tính bằng công thức:
\[
W = \frac{1}{2} k \cdot (\Delta x)^2
\]
Trong đó:
- \( W \): Năng lượng đàn hồi (đơn vị: Joule, J)
- \( k \): Hằng số đàn hồi
- \( \Delta x \): Độ biến dạng của lò xo
- Công thức lực đàn hồi trong vật liệu: Đối với một thanh vật liệu đàn hồi, lực đàn hồi có thể được tính bằng công thức:
\[
F = Y \cdot \frac{A \cdot \Delta L}{L_0}
\]
Trong đó:
- \( F \): Lực đàn hồi (N)
- \( Y \): Suất đàn hồi của vật liệu (Pa)
- \( A \): Diện tích mặt cắt ngang của thanh (m²)
- \( \Delta L \): Độ biến dạng của thanh (m)
- \( L_0 \): Chiều dài ban đầu của thanh (m)
Các công thức trên cung cấp nền tảng cơ bản để tính toán và hiểu rõ hơn về lực đàn hồi trong các vật liệu và ứng dụng thực tiễn. Nắm vững các công thức này giúp bạn áp dụng một cách hiệu quả trong các bài toán thực tế và thiết kế kỹ thuật.