Chủ đề lực đàn hồi và lực phục hồi: Lực đàn hồi và lực phục hồi là hai khái niệm quan trọng trong vật lý, liên quan mật thiết đến các hiện tượng cơ học. Bài viết này sẽ giúp bạn hiểu rõ về lực đàn hồi và lực phục hồi, từ định nghĩa, công thức tính toán cho đến ứng dụng thực tiễn trong đời sống và công nghiệp.
Mục lục
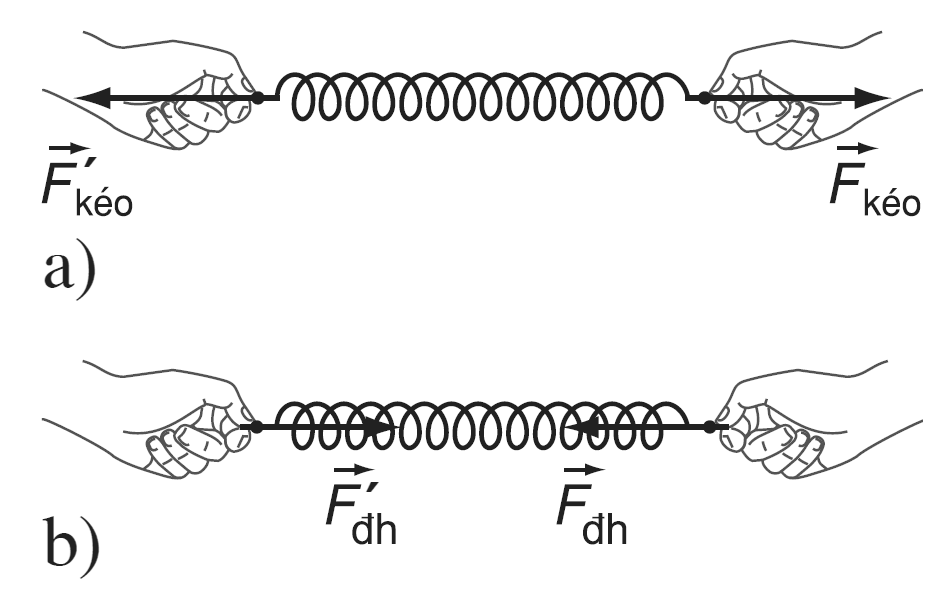
Khái niệm về Lực Đàn Hồi và Lực Phục Hồi
Lực đàn hồi là lực xuất hiện khi một vật bị biến dạng (bị nén hoặc kéo dãn) và có xu hướng phục hồi lại trạng thái ban đầu. Lực này có thể được biểu thị bằng định luật Hooke:
Trong đó:
- F là lực đàn hồi (N).
- k là hằng số đàn hồi của lò xo (N/m).
- x là độ biến dạng của lò xo (m).
Công thức và Ứng dụng của Lực Đàn Hồi
- Lực đàn hồi tối đa:
- Lực đàn hồi tối thiểu:
Ứng dụng của lực đàn hồi rất đa dạng, từ hệ thống treo của xe hơi, lò xo trong bút bi, đến các thiết bị y tế và thể thao. Lực này giúp duy trì cân bằng và ổn định trong nhiều thiết bị cơ học.
Lực Phục Hồi
Lực phục hồi là lực xuất hiện khi một vật bị biến dạng và có xu hướng trở về vị trí cân bằng ban đầu. Đây là một yếu tố quan trọng trong dao động điều hòa, với công thức cơ bản:
- Lực phục hồi cực đại:
- Lực phục hồi cực tiểu:
Lực phục hồi được ứng dụng trong các hệ thống dao động như con lắc lò xo, nơi lực này giúp duy trì chuyển động đều đặn và ổn định.
Bài Tập và Ứng Dụng Thực Tiễn
Dưới đây là một số bài tập và ứng dụng cụ thể liên quan đến lực đàn hồi và lực phục hồi:
- Một lò xo có độ cứng k = 100 N/m và bị kéo dãn 0.05 m. Hãy tính lực đàn hồi.
- Một con lắc lò xo có khối lượng m = 0.5 kg, lò xo có độ cứng k = 200 N/m. Hãy tính lực phục hồi khi con lắc ở vị trí cách vị trí cân bằng x = 0.05 m.
Những bài tập này giúp làm quen với các khái niệm và công thức liên quan, từ đó hiểu rõ hơn về lực đàn hồi và lực phục hồi trong các hệ thống cơ học.

.png)
1. Khái Niệm về Lực Đàn Hồi
Lực đàn hồi là một khái niệm cơ bản trong vật lý học, mô tả lực xuất hiện khi một vật bị biến dạng và có xu hướng trở về trạng thái ban đầu. Lực này có vai trò quan trọng trong nhiều hiện tượng và ứng dụng thực tế, từ hệ thống treo trong xe hơi đến các thiết bị y tế.
Trong vật lý, lực đàn hồi thường được mô tả bằng định luật Hooke, được phát biểu như sau:
- F: Lực đàn hồi (đơn vị: Newton, N).
- k: Hằng số đàn hồi của vật liệu hoặc lò xo (đơn vị: N/m).
- x: Độ biến dạng của vật (đơn vị: mét, m).
Khi một vật bị nén hoặc kéo dãn, lực đàn hồi sẽ xuất hiện để chống lại sự biến dạng đó. Độ lớn của lực này tỷ lệ thuận với độ biến dạng và được xác định bởi hằng số đàn hồi k của vật liệu. Đối với lò xo, k càng lớn thì lò xo càng cứng và lực đàn hồi càng mạnh.
Lực đàn hồi có nhiều ứng dụng trong đời sống, như giúp các hệ thống cơ học duy trì sự cân bằng, giảm chấn động trong hệ thống treo của xe hơi, và tạo lực đẩy trong các thiết bị như bút bi hoặc đồng hồ cơ.
Ví dụ, khi bạn nén hoặc kéo dãn một lò xo, lực đàn hồi sẽ xuất hiện để kéo lò xo trở về chiều dài ban đầu. Càng kéo dài lò xo, lực đàn hồi càng tăng, tuân theo định luật Hooke cho đến khi lò xo vượt quá giới hạn đàn hồi và biến dạng vĩnh viễn.
2. Khái Niệm về Lực Phục Hồi
Lực phục hồi là lực xuất hiện khi một vật bị biến dạng và có xu hướng trở về trạng thái cân bằng ban đầu. Đây là một trong những yếu tố quan trọng trong dao động điều hòa, đặc biệt trong các hệ thống có chuyển động lặp lại, như con lắc hoặc lò xo.
Khi một vật như lò xo hoặc dây đàn bị kéo dãn hoặc nén lại, lực phục hồi sẽ hoạt động để đưa vật về vị trí ban đầu. Lực này cũng tuân theo định luật Hooke trong phạm vi đàn hồi của vật liệu. Định luật này có thể được biểu diễn như sau:
- F: Lực phục hồi (đơn vị: Newton, N).
- k: Hằng số đàn hồi của vật liệu hoặc lò xo (đơn vị: N/m).
- x: Độ biến dạng của vật (đơn vị: mét, m).
Trong dao động điều hòa, lực phục hồi đóng vai trò là lực chính giúp duy trì chuyển động lặp lại. Khi vật dao động vượt qua vị trí cân bằng, lực phục hồi liên tục đổi chiều, tạo ra một lực đối ngược với chiều chuyển động, làm cho vật dao động qua lại xung quanh vị trí cân bằng.
Ví dụ, trong một hệ con lắc đơn, khi con lắc được kéo lệch khỏi vị trí cân bằng, trọng lực và lực căng dây sẽ tạo ra một lực phục hồi kéo con lắc trở về vị trí ban đầu. Lực này giúp duy trì dao động của con lắc theo thời gian.
Lực phục hồi không chỉ có vai trò trong các hệ thống dao động mà còn được áp dụng trong nhiều lĩnh vực khác như cơ học, kỹ thuật và thiết kế, nơi việc kiểm soát và dự đoán dao động là cần thiết.

3. Công Thức Tính Toán Lực Đàn Hồi và Lực Phục Hồi
Trong vật lý, lực đàn hồi và lực phục hồi là hai khái niệm quan trọng liên quan đến sự biến dạng của các vật liệu đàn hồi. Các công thức tính toán dưới đây giúp xác định giá trị của các lực này dựa trên đặc điểm của vật liệu và sự biến dạng mà chúng trải qua.
3.1 Công Thức Tính Lực Đàn Hồi
Lực đàn hồi \( F_{đh} \) được xác định dựa trên định luật Hooke, theo đó lực đàn hồi tỉ lệ thuận với độ biến dạng của vật liệu. Công thức cơ bản là:
\( F_{đh} = k \cdot \Delta x \)
Trong đó:
- \( F_{đh} \) là lực đàn hồi (N).
- \( k \) là hằng số đàn hồi của vật liệu, còn được gọi là độ cứng hoặc hệ số đàn hồi của lò xo (N/m).
- \( \Delta x \) là độ biến dạng của vật (m), thường là độ dãn hoặc nén của lò xo.
Ví dụ: Nếu một lò xo có độ cứng \( k = 100 \, N/m \) và bị kéo dãn một đoạn \( \Delta x = 0.05 \, m \), lực đàn hồi sẽ là:
\( F_{đh} = 100 \times 0.05 = 5 \, N \)
3.2 Công Thức Tính Lực Phục Hồi
Lực phục hồi \( F_{ph} \) là lực giúp vật trở lại trạng thái cân bằng sau khi bị biến dạng. Đối với các hệ dao động như con lắc lò xo, lực phục hồi có công thức:
\( F_{ph} = -k \cdot \Delta x \)
Trong đó:
- Giá trị âm (-) chỉ ra rằng lực phục hồi luôn hướng ngược lại với chiều biến dạng.
Ví dụ: Một lò xo có độ cứng \( k = 50 \, N/m \) và bị nén một đoạn \( \Delta x = 0.02 \, m \), lực phục hồi sẽ là:
\( F_{ph} = -50 \times 0.02 = -1 \, N \)
3.3 Bài Tập Minh Họa Tính Toán Lực Đàn Hồi và Lực Phục Hồi
Dưới đây là một ví dụ minh họa cụ thể:
- Một lò xo có hằng số \( k = 200 \, N/m \) bị kéo dãn một đoạn \( \Delta x = 0.1 \, m \). Tính lực đàn hồi.
- Một con lắc lò xo với \( k = 150 \, N/m \) bị nén \( 0.05 \, m \). Tính lực phục hồi.
Giải:
- Lực đàn hồi: \( F_{đh} = 200 \times 0.1 = 20 \, N \).
- Lực phục hồi: \( F_{ph} = -150 \times 0.05 = -7.5 \, N \).

XEM THÊM:
4. Ứng Dụng Thực Tiễn của Lực Đàn Hồi và Lực Phục Hồi
Lực đàn hồi và lực phục hồi không chỉ là các khái niệm quan trọng trong vật lý mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày cũng như trong công nghiệp. Dưới đây là một số ứng dụng cụ thể:
- Hệ thống treo trong ô tô:
Trong các phương tiện giao thông, lực đàn hồi được sử dụng trong hệ thống treo giúp giảm thiểu rung động và sốc khi di chuyển trên các bề mặt không bằng phẳng. Nhờ đó, hành khách có một chuyến đi êm ái và thoải mái hơn.
- Bút bi:
Lực đàn hồi của lò xo trong bút bi nhấn giúp điều khiển việc thụt ruột bút vào và ra. Đây là một ứng dụng phổ biến và thiết thực trong đời sống hàng ngày.
- Đồng hồ cơ học:
Lực đàn hồi của lò xo trong đồng hồ cơ học giúp giữ và phát hành năng lượng đều đặn, đảm bảo đồng hồ hoạt động chính xác. Đây là nguyên lý cơ bản trong hầu hết các loại đồng hồ cơ.
- Dụng cụ thể thao:
Các thiết bị thể thao, như máy tập gym hoặc dụng cụ chơi golf, thường sử dụng lò xo đàn hồi để tăng cường hiệu suất và giảm nguy cơ chấn thương cho người chơi.
- Công nghiệp sản xuất:
Trong các dây chuyền sản xuất, lò xo đàn hồi được sử dụng để hấp thụ rung động, duy trì áp lực hoặc lực kéo nhất định, từ đó đảm bảo quy trình sản xuất diễn ra ổn định và hiệu quả.
- Thiết bị y tế:
Các lò xo đàn hồi được ứng dụng trong nhiều thiết bị y tế, từ máy đo huyết áp đến các thiết bị hỗ trợ tim mạch, giúp nâng cao hiệu quả và độ tin cậy trong việc điều trị bệnh.
- Công nghệ điện tử:
Lò xo đàn hồi được sử dụng trong các thiết bị điện tử để tạo ra kết nối đáng tin cậy giữa các linh kiện, giúp thiết bị hoạt động ổn định và bền bỉ hơn.
Những ứng dụng trên cho thấy rằng lực đàn hồi và lực phục hồi đóng vai trò quan trọng trong nhiều lĩnh vực, từ đời sống hàng ngày đến công nghiệp và y tế. Nhờ vào những nguyên lý này, nhiều thiết bị và hệ thống đã được phát triển để cải thiện chất lượng cuộc sống và hiệu quả sản xuất.

5. Bài Tập và Ví Dụ Về Lực Đàn Hồi và Lực Phục Hồi
Dưới đây là một số bài tập và ví dụ thực tế giúp bạn hiểu rõ hơn về lực đàn hồi và lực phục hồi cũng như cách tính toán và ứng dụng chúng trong thực tiễn.
5.1 Bài tập tính lực đàn hồi
- Bài tập 1: Một lò xo có độ cứng \( k = 150 \, \text{N/m} \), bị kéo dãn \( 0,1 \, \text{m} \). Tính lực đàn hồi của lò xo.
Giải:Sử dụng công thức \( F_{đh} = -kx \)
Thay các giá trị vào công thức:
\[
F_{đh} = -150 \times 0,1 = -15 \, \text{N}
\]Vậy lực đàn hồi của lò xo là \( 15 \, \text{N} \).
- Bài tập 2: Xác định độ giãn của lò xo khi một vật nặng \( 3 \, \text{kg} \) treo thẳng đứng lên lò xo có độ cứng \( k = 200 \, \text{N/m} \) ở trạng thái cân bằng (lấy \( g = 9,8 \, \text{m/s}^2 \)).
Giải:Sử dụng công thức \( F_{đh} = mg \)
Thay các giá trị vào công thức:
\[
kx = mg \Rightarrow x = \frac{mg}{k} = \frac{3 \times 9,8}{200} = 0,147 \, \text{m}
\]Vậy độ giãn của lò xo là \( 0,147 \, \text{m} \).
5.2 Bài tập tính lực phục hồi
- Bài tập 1: Một lò xo có độ cứng \( k = 100 \, \text{N/m} \), dao động với biên độ \( A = 0,05 \, \text{m} \). Tính giá trị cực đại của lực phục hồi.
Giải:Sử dụng công thức \( F_{\text{max}} = kA \)
Thay các giá trị vào công thức:
\[
F_{\text{max}} = 100 \times 0,05 = 5 \, \text{N}
\]Vậy lực phục hồi cực đại là \( 5 \, \text{N} \).
- Bài tập 2: Một con lắc lò xo treo thẳng đứng dao động với biên độ \( A = 0,1 \, \text{m} \), biết tỉ số giữa lực cực đại và lực cực tiểu là 4. Tính độ giãn của lò xo khi vật ở vị trí cân bằng.
Giải:Ta có tỉ số lực:
\[
\frac{F_{\text{max}}}{F_{\text{min}}} = 4
\]Sử dụng công thức lực phục hồi cực đại:
\[
F_{\text{max}} = k(A + x)
\]Vậy độ giãn của lò xo là:
\[
x = \frac{F_{\text{max}}}{k} - A = 0,1 \, \text{m}
\]
5.3 Ví dụ thực tế về lực đàn hồi và lực phục hồi
Một ví dụ thực tế về lực đàn hồi là hệ thống treo trong ô tô, nơi lò xo hấp thụ xung lực từ mặt đường để duy trì độ ổn định và thoải mái cho hành khách.
Trong dao động cơ học, lực phục hồi xuất hiện trong con lắc lò xo giúp điều chỉnh dao động và đưa vật trở về vị trí cân bằng sau khi bị tác động.