Lực Đàn Hồi Tác Dụng Lên Điểm Treo: Khám Phá Toàn Diện và Ứng Dụng Thực Tiễn

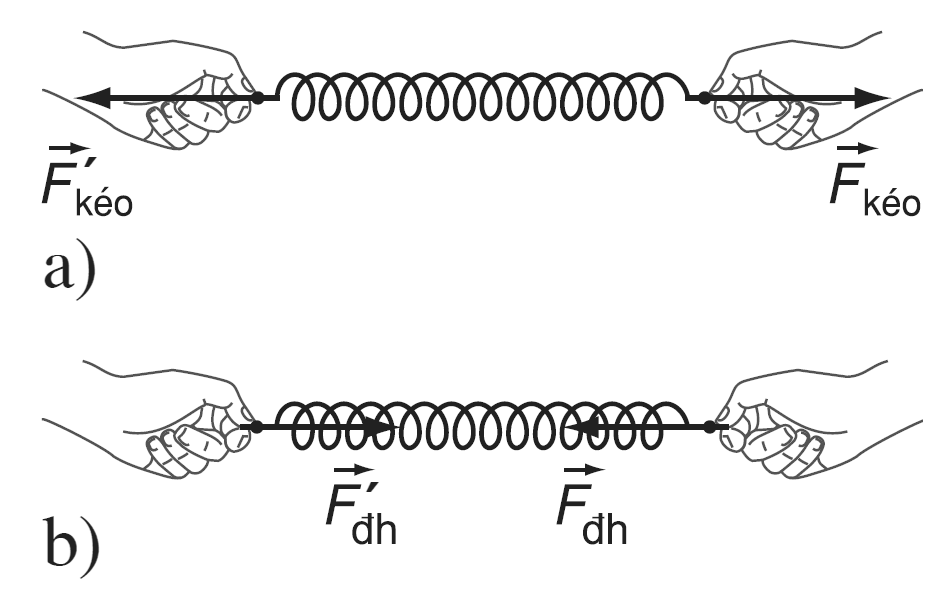
Lực đàn hồi là một khái niệm quan trọng trong vật lý học, đặc biệt liên quan đến chuyển động dao động của các vật thể. Khi một vật thể như lò xo bị kéo dãn hoặc nén, lực đàn hồi sẽ xuất hiện để đưa vật thể trở lại vị trí cân bằng ban đầu. Lực này có phương và chiều phụ thuộc vào hướng biến dạng của lò xo.

1. Định Nghĩa và Công Thức Tính Lực Đàn Hồi

Lực đàn hồi (F) có thể được định nghĩa qua định luật Hooke, biểu thức như sau:

\[
F = -k \cdot \Delta x
\]

Trong đó:

• k: Độ cứng của lò xo (N/m).
• \(\Delta x\): Độ biến dạng của lò xo so với vị trí cân bằng (m).
• Dấu âm thể hiện lực đàn hồi luôn có hướng ngược lại với chiều biến dạng.

2. Lực Đàn Hồi Tác Dụng Lên Điểm Treo

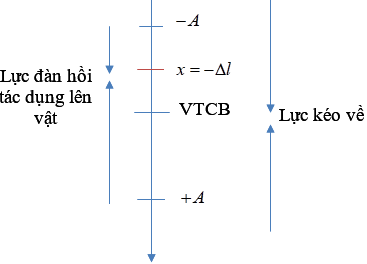
Khi lò xo bị biến dạng, điểm treo (nơi lò xo gắn cố định) sẽ chịu tác dụng của lực đàn hồi. Lực này luôn hướng lên nếu lò xo bị kéo dãn và hướng xuống nếu lò xo bị nén. Đối với một hệ lò xo treo thẳng đứng, lực đàn hồi cân bằng với trọng lực tác dụng lên vật nặng ở đầu kia của lò xo.

3. Ứng Dụng của Lực Đàn Hồi Trong Thực Tế

Lực đàn hồi có nhiều ứng dụng thực tiễn trong cuộc sống:

• Trong công nghệ: Các loại lò xo được sử dụng trong nhiều thiết bị cơ khí, chẳng hạn như giảm xóc trong xe cộ, đồng hồ cơ, và ghế ngồi.
• Trong xây dựng: Lực đàn hồi của vật liệu xây dựng (như bê tông và thép) được tính toán để đảm bảo tính ổn định và an toàn của các công trình.
• Trong y học: Lực đàn hồi của các thiết bị y tế như băng nẹp và đai hỗ trợ giúp điều chỉnh các vấn đề cơ xương.

4. Các Bài Toán Liên Quan Đến Lực Đàn Hồi

Các bài toán về lực đàn hồi thường liên quan đến việc tính toán biên độ dao động, tần số dao động của các vật gắn vào lò xo, và lực tác dụng lên điểm treo trong các tình huống dao động điều hòa. Ví dụ, một bài toán có thể yêu cầu tính lực đàn hồi khi biết độ cứng của lò xo và độ biến dạng của nó trong một chu kỳ dao động.

5. Kết Luận

Hiểu rõ về lực đàn hồi và cách nó tác dụng lên điểm treo không chỉ giúp giải quyết các bài toán vật lý một cách dễ dàng mà còn giúp áp dụng vào thực tế một cách hiệu quả. Từ việc tính toán sức bền của các công trình xây dựng đến cải thiện chất lượng cuộc sống qua các thiết bị hàng ngày, lực đàn hồi đóng vai trò quan trọng trong nhiều lĩnh vực.

Lực đàn hồi là lực xuất hiện khi một vật thể bị biến dạng (kéo dãn hoặc nén) và có xu hướng đưa vật trở lại hình dạng ban đầu. Trong hệ thống lò xo, lực đàn hồi tuân theo định luật Hooke, được biểu diễn bằng công thức:

\[
F = -k \cdot \Delta x
\]

• F: Lực đàn hồi (N).
• k: Hằng số đàn hồi của lò xo (N/m), đặc trưng cho độ cứng của lò xo.
• \(\Delta x\): Độ biến dạng của lò xo so với vị trí cân bằng (m).

Dấu âm trong công thức thể hiện lực đàn hồi luôn có chiều ngược lại với hướng của lực gây biến dạng. Nếu lò xo bị kéo dãn, lực đàn hồi sẽ hướng về phía làm lò xo co lại. Ngược lại, nếu lò xo bị nén, lực đàn hồi sẽ hướng về phía làm lò xo dãn ra.

Trong trường hợp một vật nặng được treo vào lò xo và kéo xuống, lực đàn hồi sẽ cân bằng với trọng lực khi vật đứng yên. Đây là nguyên tắc cơ bản để tính toán lực đàn hồi trong các hệ thống cơ học và trong các bài toán dao động.

Khái niệm lực đàn hồi không chỉ quan trọng trong việc giải thích hiện tượng vật lý mà còn ứng dụng trong nhiều lĩnh vực khác nhau như thiết kế cơ khí, xây dựng, và các thiết bị công nghệ cao.

Lực đàn hồi xuất hiện trong hệ lò xo khi lò xo bị kéo dãn hoặc nén. Khi một vật được treo vào lò xo, điểm treo của lò xo sẽ chịu tác dụng của lực đàn hồi. Cơ chế tác dụng này có thể được hiểu qua các bước sau:

1. Biến dạng của lò xo: Khi vật nặng được treo vào lò xo, trọng lực của vật làm lò xo dãn ra. Độ biến dạng của lò xo phụ thuộc vào trọng lượng của vật và độ cứng của lò xo.
2. Xuất hiện lực đàn hồi: Theo định luật Hooke, khi lò xo bị biến dạng, lực đàn hồi xuất hiện và có chiều ngược lại với chiều của lực gây biến dạng. Lực này có giá trị:

   
   \[
   F = -k \cdot \Delta x
   \]

3. Cân bằng lực: Trong trạng thái cân bằng, lực đàn hồi mà lò xo tác dụng lên điểm treo sẽ bằng với trọng lực của vật nặng. Khi đó, lò xo sẽ dừng lại ở một vị trí nhất định, và vật treo sẽ đứng yên.
4. Dao động điều hòa: Nếu vật nặng được kéo xuống hoặc nâng lên rồi thả ra, nó sẽ dao động xung quanh vị trí cân bằng. Trong quá trình dao động, lực đàn hồi thay đổi liên tục và luôn hướng về vị trí cân bằng, làm cho vật dao động điều hòa.

Như vậy, lực đàn hồi không chỉ ảnh hưởng đến điểm treo mà còn quyết định trạng thái chuyển động và dao động của hệ thống lò xo và vật treo.

Lực đàn hồi có nhiều ứng dụng quan trọng trong đời sống và kỹ thuật, đặc biệt là trong việc thiết kế các thiết bị cơ học và xây dựng. Dưới đây là một số ứng dụng thực tiễn của lực đàn hồi:

• Trong công nghệ và kỹ thuật: Lực đàn hồi được sử dụng trong các hệ thống giảm xóc của xe cộ, giúp hấp thụ lực va chạm và đảm bảo chuyến đi êm ái. Ngoài ra, các lò xo cũng được sử dụng trong các thiết bị như đồng hồ, khóa cửa và ghế ngồi để tạo ra sự linh hoạt và đàn hồi cần thiết.
• Trong xây dựng và kiến trúc: Lực đàn hồi của các vật liệu xây dựng như thép và bê tông được tính toán kỹ lưỡng để đảm bảo rằng các công trình có thể chịu được tải trọng và các yếu tố ngoại lực mà không bị biến dạng vĩnh viễn. Điều này giúp tăng độ bền và tuổi thọ của các công trình.
• Trong y học: Các thiết bị y tế như băng nẹp, đai lưng và dụng cụ chỉnh hình sử dụng lực đàn hồi để hỗ trợ và điều chỉnh các bộ phận cơ thể, giúp phục hồi chức năng và cải thiện sức khỏe cho bệnh nhân.
• Trong đời sống hàng ngày: Lực đàn hồi cũng xuất hiện trong nhiều thiết bị gia dụng như đệm lò xo, bút bi, và đồ chơi trẻ em. Những sản phẩm này tận dụng tính chất đàn hồi để mang lại sự tiện lợi và thoải mái cho người dùng.

Nhờ những ứng dụng đa dạng, lực đàn hồi không chỉ là một khái niệm vật lý mà còn là yếu tố quan trọng trong nhiều khía cạnh của cuộc sống hiện đại.

Bài toán thực hành về lực đàn hồi là một phần quan trọng giúp học sinh và sinh viên hiểu rõ hơn về cách áp dụng lý thuyết vào thực tế. Dưới đây là một số bài toán phổ biến và hướng dẫn cách giải chúng:

1. Bài toán 1: Tính lực đàn hồi trong hệ lò xo treo thẳng đứng

   Giả sử một lò xo có độ cứng \( k \) (N/m) được treo thẳng đứng và một vật có khối lượng \( m \) (kg) được treo vào lò xo, hãy tính lực đàn hồi khi lò xo đạt trạng thái cân bằng.

   • Bước 1: Xác định trọng lực tác dụng lên vật: \[ F_g = m \cdot g \] Trong đó \( g \) là gia tốc trọng trường (khoảng 9,8 m/s²).
   • Bước 2: Ở trạng thái cân bằng, lực đàn hồi \( F \) bằng với trọng lực, do đó: \[ F = F_g = m \cdot g \]
   • Bước 3: Sử dụng định luật Hooke để tính độ dãn của lò xo: \[ \Delta x = \frac{F}{k} = \frac{m \cdot g}{k} \]
2. Bài toán 2: Dao động điều hòa của lò xo

   Cho một lò xo có độ cứng \( k \) và một vật nặng \( m \) được gắn vào lò xo, nếu vật được kéo dãn một đoạn \( A \) rồi thả ra, hãy tính chu kỳ dao động của hệ.

   • Bước 1: Xác định tần số góc của dao động: \[ \omega = \sqrt{\frac{k}{m}} \]
   • Bước 2: Tính chu kỳ dao động: \[ T = 2\pi \sqrt{\frac{m}{k}} \]
   • Bước 3: Xác định phương trình dao động: \[ x(t) = A \cos(\omega t + \phi) \] Trong đó \( \phi \) là pha ban đầu, có thể xác định dựa trên điều kiện ban đầu của bài toán.

Những bài toán trên giúp củng cố kiến thức về lực đàn hồi và cách áp dụng định luật Hooke vào các hệ thống cơ học thực tế, đồng thời cung cấp nền tảng vững chắc cho việc giải quyết các bài toán phức tạp hơn.

Lực đàn hồi đóng vai trò vô cùng quan trọng trong nhiều lĩnh vực khoa học và ứng dụng thực tiễn. Sự tồn tại của lực đàn hồi không chỉ giúp duy trì sự cân bằng trong các hệ thống cơ học mà còn là yếu tố quyết định trong nhiều thiết kế kỹ thuật, xây dựng, và y học.

Lực Đàn Hồi và Sự Ổn Định Của Hệ Thống:

• Lực đàn hồi giúp duy trì vị trí cân bằng của các vật thể, đặc biệt là trong các hệ thống lò xo. Nó đóng vai trò quan trọng trong việc ngăn chặn các dao động không mong muốn, từ đó giữ cho các hệ thống ổn định.
• Trong hệ thống treo của các phương tiện giao thông, lực đàn hồi giúp hấp thụ các chấn động từ mặt đường, mang lại sự êm ái cho người sử dụng.

Ứng Dụng Trong Kỹ Thuật và Công Nghệ:

• Trong kỹ thuật, lực đàn hồi được áp dụng rộng rãi trong việc thiết kế các bộ phận giảm chấn, lò xo trong máy móc và thiết bị. Nó giúp tối ưu hóa sự hoạt động của các hệ thống cơ khí, đảm bảo sự bền bỉ và hiệu suất cao.
• Lực đàn hồi cũng có vai trò quan trọng trong các thiết bị như đồng hồ cơ học, nơi mà nó giúp điều chỉnh và duy trì sự chính xác của thời gian.

Tầm Quan Trọng Trong Đời Sống và Y Học:

• Trong y học, lực đàn hồi được ứng dụng để chế tạo các thiết bị hỗ trợ vận động như băng đàn hồi, nẹp và các dụng cụ chỉnh hình, giúp cải thiện chất lượng cuộc sống cho bệnh nhân.
• Trong đời sống hàng ngày, lực đàn hồi hiện diện trong các đồ vật như nệm lò xo, ghế tựa, giúp tăng cường sự thoải mái và sức khỏe cho người sử dụng.

Tóm lại, lực đàn hồi không chỉ là một khái niệm vật lý cơ bản mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống và công nghệ. Việc hiểu rõ và áp dụng lực đàn hồi một cách hiệu quả sẽ góp phần quan trọng vào sự phát triển bền vững và tiện nghi của xã hội.