Lực Đàn Hồi Lớp 12: Tất Tần Tật Kiến Thức Và Bài Tập Thực Hành

Lực đàn hồi là một trong những khái niệm cơ bản trong chương trình Vật lý lớp 12. Nội dung này chủ yếu tập trung vào lực đàn hồi của lò xo và định luật Húc. Dưới đây là các khái niệm chính và ứng dụng của lực đàn hồi.

1. Định Nghĩa Lực Đàn Hồi

Lực đàn hồi là lực xuất hiện khi một vật đàn hồi bị biến dạng (bị kéo dãn hoặc bị nén lại). Lực này có xu hướng làm cho vật trở lại trạng thái ban đầu của nó.

2. Định Luật Húc

Định luật Húc phát biểu rằng: Trong giới hạn đàn hồi, độ lớn của lực đàn hồi do lò xo sinh ra tỷ lệ thuận với độ biến dạng của lò xo:

$$F_{đàn hồi} = k \cdot \Delta l$$

• \(F_{đàn hồi}\): Lực đàn hồi (N)
• \(k\): Hệ số đàn hồi của lò xo (N/m)
• \(\Delta l\): Độ biến dạng của lò xo (m)

3. Ứng Dụng Thực Tế

Lực đàn hồi có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật:

• Trong kỹ thuật: Lò xo được sử dụng trong hệ thống giảm chấn của ô tô, xe máy và các thiết bị cơ khí khác.
• Trong đời sống hàng ngày: Lực đàn hồi giúp tạo sự thoải mái khi ngồi trên ghế sofa hay nằm trên nệm lò xo.
• Trong thể thao: Lực đàn hồi hỗ trợ trong các môn như nhảy sào, bắn cung, tạo lực cho các dụng cụ thể thao.
• Trong y học: Ứng dụng trong các thiết bị hỗ trợ và máy tập phục hồi chức năng.

4. Ví Dụ Bài Tập

Dưới đây là ví dụ về một bài tập vận dụng định luật Húc:

Giả sử một lò xo có chiều dài tự nhiên là 30cm. Khi treo một vật có khối lượng 100g, chiều dài của lò xo tăng lên 35cm. Hỏi độ cứng của lò xo là bao nhiêu?

$$k = \frac{mg}{\Delta l}$$

Trong đó:

• \(m = 0.1 kg\)
• \(g = 9.8 m/s^2\)
• \(\Delta l = 0.05 m\)

Từ đó, ta tính được độ cứng của lò xo:

$$k = \frac{0.1 \cdot 9.8}{0.05} = 19.6 \, N/m$$

5. Bài Tập Ôn Luyện

1. Một lò xo có hệ số đàn hồi \(k = 200 N/m\). Tính lực đàn hồi khi lò xo bị kéo dãn \(0.1m\).
2. Một vật có khối lượng \(2kg\) được treo vào lò xo có hệ số đàn hồi \(k = 150 N/m\). Tính độ dãn của lò xo.

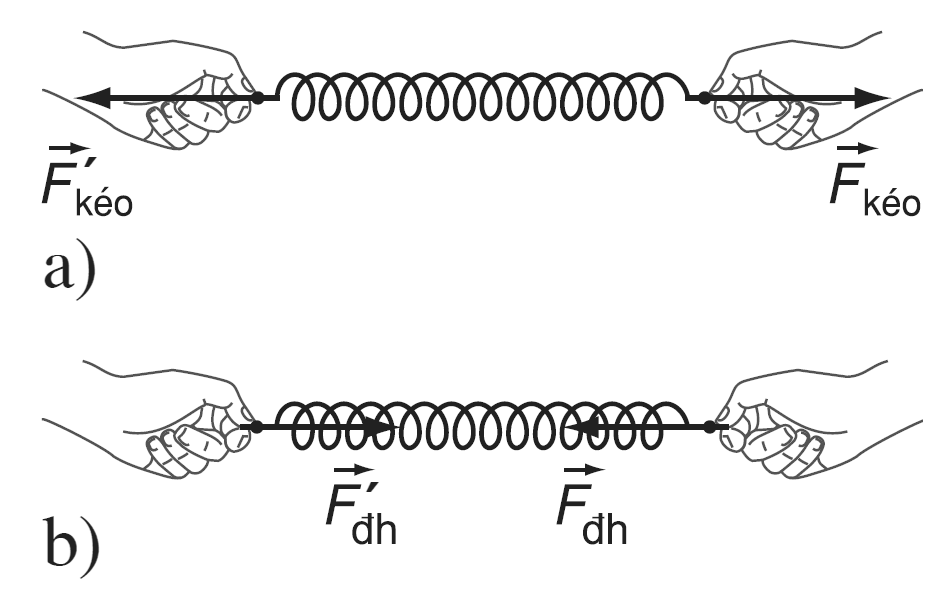
Lực đàn hồi là lực được sinh ra khi một vật bị biến dạng đàn hồi, chẳng hạn như khi một lò xo bị kéo dài hoặc nén lại. Để tính toán lực đàn hồi, chúng ta sử dụng định luật Hooke:

Lực đàn hồi trong lò xo

Định luật Hooke phát biểu rằng lực đàn hồi F tỷ lệ thuận với độ biến dạng của lò xo:

$$
F
=
-
k
x

• F: Lực đàn hồi (N).
• k: Hằng số lò xo (N/m).
• x: Độ biến dạng của lò xo (m).

Dấu trừ trong công thức thể hiện rằng lực đàn hồi luôn hướng ngược lại với hướng biến dạng.

Biểu thức lực đàn hồi

Khi lò xo bị kéo dài hoặc nén lại một đoạn x so với vị trí cân bằng, lực đàn hồi sẽ có giá trị:

$$
F
=
-
k
x

Trong đó:

• Giá trị của x có thể là dương (khi lò xo bị kéo dài) hoặc âm (khi lò xo bị nén).
• Hằng số k phụ thuộc vào đặc tính của lò xo, thường được xác định thông qua thực nghiệm.

Các đại lượng ảnh hưởng đến lực đàn hồi

Lực đàn hồi phụ thuộc vào các yếu tố sau:

1. Độ cứng của lò xo: Được biểu thị bằng hằng số k, độ cứng càng lớn thì lực đàn hồi càng mạnh.
2. Độ biến dạng x: Độ biến dạng càng lớn thì lực đàn hồi càng lớn.
3. Loại vật liệu: Lò xo làm từ các vật liệu khác nhau sẽ có hằng số k khác nhau.

Như vậy, để tính toán chính xác lực đàn hồi, cần biết các giá trị cụ thể của hằng số k và độ biến dạng x.

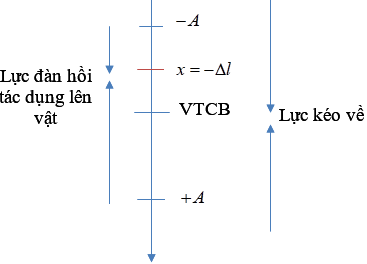
Lực hồi phục và lực kéo về là hai khái niệm quan trọng trong cơ học, đặc biệt khi nghiên cứu về con lắc lò xo và các hệ dao động điều hòa.

Khái niệm và định nghĩa

Lực hồi phục là lực có xu hướng đưa vật trở lại vị trí cân bằng khi vật bị lệch khỏi vị trí này. Lực hồi phục luôn có chiều hướng về vị trí cân bằng và có độ lớn tỷ lệ với độ biến dạng của lò xo hoặc hệ dao động. Công thức lực hồi phục thường được viết dưới dạng:

\( F_{hp} = -k \cdot x \)

Trong đó:

• \(F_{hp}\): Lực hồi phục
• \(k\): Độ cứng của lò xo
• \(x\): Độ biến dạng của lò xo so với vị trí cân bằng

Lực kéo về thực chất là một trường hợp cụ thể của lực hồi phục. Khi xét dao động điều hòa, lực kéo về là lực tác động làm vật dao động điều hòa quanh vị trí cân bằng. Công thức tổng quát của lực kéo về cũng được viết dưới dạng:

\( F_{kv} = -k \cdot x \)

Sự khác biệt giữa lực kéo về và lực đàn hồi

Cả lực kéo về và lực đàn hồi đều là các lực hồi phục. Tuy nhiên, lực kéo về là trường hợp đặc biệt khi vật tham gia vào dao động điều hòa, còn lực đàn hồi có thể tồn tại trong nhiều hoàn cảnh khác nhau như trong lò xo hoặc các hệ vật lý khác.

Ứng dụng của lực hồi phục trong bài tập

Trong các bài toán liên quan đến con lắc lò xo, lực hồi phục và lực kéo về đóng vai trò quyết định trong việc xác định chuyển động của vật. Ví dụ, khi tính toán độ giãn, độ nén của lò xo, hoặc khi phân tích lực tác động lên vật trong dao động điều hòa, các công thức liên quan đến lực hồi phục và lực kéo về sẽ được sử dụng để giải quyết bài toán.

Với hiểu biết về các công thức này, học sinh có thể áp dụng chúng vào nhiều bài toán vật lý khác nhau, từ đơn giản đến phức tạp, đồng thời hiểu rõ hơn về cơ chế hoạt động của các hệ dao động trong thực tế.

Con lắc lò xo là một hệ cơ học bao gồm một vật nhỏ gắn vào một lò xo, có khả năng dao động điều hòa dưới tác dụng của lực đàn hồi. Lực đàn hồi trong con lắc lò xo đóng vai trò quan trọng trong việc tạo ra và duy trì dao động của hệ.

Dao động của con lắc lò xo

Khi con lắc lò xo dao động, lực đàn hồi được tạo ra bởi sự biến dạng của lò xo và tuân theo định luật Hooke:

F = -kx

Trong đó:

• F: lực đàn hồi (N)
• k: độ cứng của lò xo (N/m)
• x: độ dãn hoặc nén của lò xo (m)

Dao động của con lắc lò xo là dao động điều hòa với tần số góc \omega được tính bằng:

\omega = \sqrt{\frac{k}{m}}

Trong đó m là khối lượng của vật nặng.

Công thức tính lực hồi phục

Lực hồi phục là lực đàn hồi trong con lắc lò xo, có xu hướng kéo vật về vị trí cân bằng:

F_h = -kx

Lực hồi phục phụ thuộc vào độ biến dạng của lò xo và luôn hướng về vị trí cân bằng.

Bài tập áp dụng lực đàn hồi và lực kéo về

Các bài tập về con lắc lò xo thường yêu cầu tính toán các đại lượng như chu kỳ, tần số, năng lượng của dao động. Một số công thức quan trọng cần ghi nhớ:

• Chu kỳ dao động: T = 2\pi\sqrt{\frac{m}{k}}
• Năng lượng của dao động: W = \frac{1}{2}kA^2

Trong đó A là biên độ dao động.

Áp dụng các công thức này để giải các bài tập liên quan đến con lắc lò xo sẽ giúp củng cố kiến thức về lực đàn hồi và lực hồi phục.

Trong các bài toán vật lý lớp 12, lực đàn hồi là một chủ đề quan trọng, đặc biệt là khi xem xét các hệ thống lò xo. Để giải quyết các bài toán này, chúng ta cần nắm vững các khái niệm cơ bản cũng như các công thức liên quan đến lực đàn hồi.

Một trong những phương pháp phổ biến là sử dụng định luật Hooke để tính lực đàn hồi. Định luật Hooke được biểu diễn bởi công thức:

\( F = -k \cdot \Delta l \)

Trong đó:

• \( F \): Lực đàn hồi (N)
• \( k \): Hằng số đàn hồi của lò xo (N/m)
• \( \Delta l \): Độ biến dạng của lò xo (m)

Khi giải quyết bài toán liên quan đến lực đàn hồi, chúng ta cần thực hiện theo các bước sau:

1. Xác định hệ thống: Đầu tiên, xác định các yếu tố như khối lượng vật nặng, độ cứng của lò xo và biên độ dao động nếu có.
2. Lập phương trình: Sử dụng định luật Hooke hoặc các phương trình cân bằng để lập phương trình liên quan đến lực đàn hồi.
3. Giải phương trình: Giải phương trình để tìm các đại lượng cần thiết như độ biến dạng, lực đàn hồi cực đại và cực tiểu.
4. Phân tích kết quả: Sau khi tính toán, cần phân tích kết quả để hiểu rõ về đặc điểm dao động của hệ thống và ứng dụng trong thực tế.

Ví dụ, với một bài toán yêu cầu tính lực đàn hồi cực đại và cực tiểu của một con lắc lò xo khi dao động, chúng ta cần biết độ cứng của lò xo \( k \), khối lượng vật nặng \( m \), và biên độ dao động \( A \). Lực đàn hồi cực đại và cực tiểu có thể được tính bằng công thức:

\( F_{max} = k \cdot (A + \Delta l) \)

\( F_{min} = k \cdot (A - \Delta l) \)

Trong đó, \( \Delta l \) là độ giãn dài của lò xo khi hệ thống ở vị trí cân bằng.

Những bước trên giúp ta phân tích và giải quyết các bài toán lực đàn hồi một cách hiệu quả, áp dụng vào nhiều tình huống thực tế trong vật lý và kỹ thuật.