Chủ đề tính lực đàn hồi của lò xo: Tìm hiểu về tính lực đàn hồi của lò xo - một khái niệm quan trọng trong vật lý. Bài viết này cung cấp cái nhìn sâu sắc về định luật Hooke, công thức tính toán, và các ứng dụng thực tiễn trong đời sống và kỹ thuật. Khám phá ngay để hiểu rõ hơn về nguyên lý hoạt động của lò xo và cách nó được sử dụng hàng ngày.
Mục lục
Tổng hợp thông tin về tính lực đàn hồi của lò xo
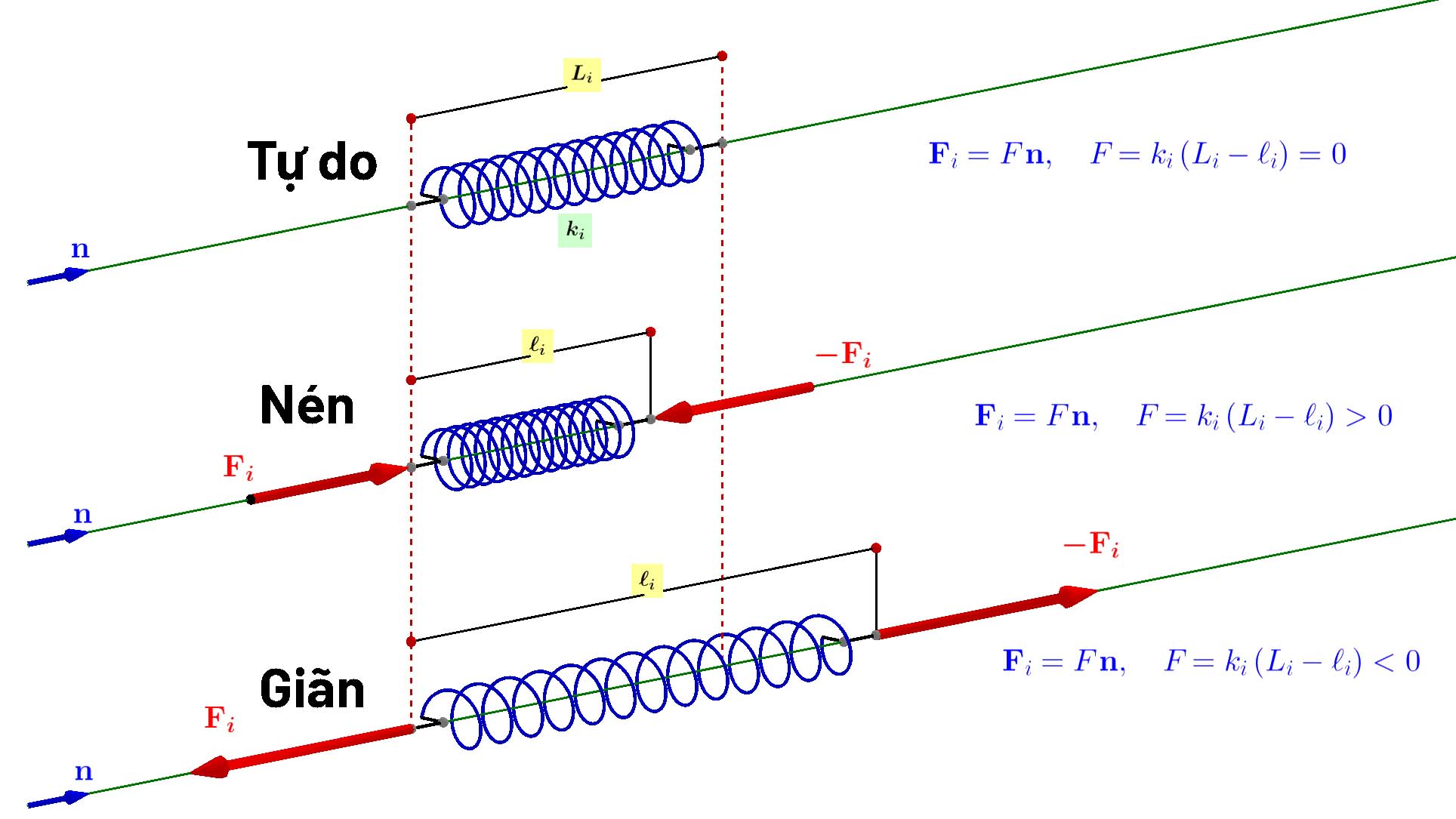
Lực đàn hồi của lò xo là một khái niệm quan trọng trong vật lý, đặc biệt trong các bài học về cơ học. Đây là lực xuất hiện khi lò xo bị biến dạng do tác dụng của một lực bên ngoài, chẳng hạn như khi lò xo bị kéo dãn hoặc nén lại. Lực đàn hồi này có xu hướng đưa lò xo trở lại trạng thái ban đầu, tức là chiều dài tự nhiên của nó.
Định luật Hooke
Định luật Hooke là cơ sở để tính toán lực đàn hồi của lò xo. Định luật này phát biểu rằng:
"Trong giới hạn đàn hồi, lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo."
Công thức của định luật Hooke được biểu diễn như sau:
\[ F = -k \cdot \Delta l \]
- F: Lực đàn hồi (Newton, N)
- k: Độ cứng của lò xo (N/m)
- \(\Delta l\): Độ biến dạng của lò xo (mét, m)
Dấu âm trong công thức cho thấy lực đàn hồi có hướng ngược với hướng của lực tác dụng gây biến dạng.
Các đại lượng liên quan đến lực đàn hồi
- Độ cứng của lò xo: Đây là một đại lượng đặc trưng cho khả năng chống lại biến dạng của lò xo. Độ cứng càng lớn thì lò xo càng khó bị kéo dãn hay nén.
- Giới hạn đàn hồi: Là giá trị lớn nhất của lực mà lò xo có thể chịu đựng mà vẫn có thể trở về trạng thái ban đầu khi lực tác dụng được gỡ bỏ. Nếu vượt quá giới hạn này, lò xo sẽ bị biến dạng vĩnh viễn.
Ứng dụng thực tiễn
Lực đàn hồi của lò xo được ứng dụng rộng rãi trong nhiều lĩnh vực, từ thiết kế các hệ thống treo trong ô tô đến sản xuất các thiết bị đo lường như lực kế. Hiểu rõ về lực đàn hồi giúp chúng ta thiết kế các thiết bị cơ học hoạt động hiệu quả và an toàn.
Ví dụ về bài tập tính lực đàn hồi của lò xo
Ví dụ: Một lò xo có độ cứng k = 200 N/m. Khi tác dụng một lực kéo 10 N vào lò xo, hãy tính độ biến dạng của lò xo.
Áp dụng công thức định luật Hooke:
\[ F = k \cdot \Delta l \Rightarrow \Delta l = \frac{F}{k} = \frac{10 \, \text{N}}{200 \, \text{N/m}} = 0,05 \, \text{m} \]
Vậy, độ biến dạng của lò xo là 0,05 m (hay 5 cm).
Kết luận
Lực đàn hồi của lò xo là một khái niệm cơ bản nhưng vô cùng quan trọng trong cơ học và các ứng dụng thực tiễn. Hiểu rõ và vận dụng đúng các công thức liên quan sẽ giúp ích rất nhiều trong học tập và nghiên cứu.

.png)
1. Giới thiệu về lực đàn hồi của lò xo
Lực đàn hồi là một trong những lực cơ bản xuất hiện khi một vật thể bị biến dạng do tác động của ngoại lực, và có xu hướng đưa vật trở về trạng thái ban đầu. Trong trường hợp của lò xo, lực đàn hồi xuất hiện khi lò xo bị kéo dài hoặc nén lại, với độ lớn tỉ lệ thuận với độ biến dạng của lò xo.
Lực đàn hồi của lò xo được miêu tả chính xác bởi Định luật Hooke, được phát biểu rằng lực đàn hồi \( F \) của lò xo tỉ lệ thuận với độ biến dạng \( \Delta l \) của lò xo, và được xác định bởi công thức:
\[
F = -k \cdot \Delta l
\]
Trong đó:
- \( F \): Lực đàn hồi (N)
- \( k \): Hằng số đàn hồi của lò xo (N/m)
- \( \Delta l \): Độ biến dạng của lò xo (m)
Định luật Hooke chỉ đúng trong giới hạn đàn hồi của lò xo, tức là khi lò xo không bị biến dạng vĩnh viễn. Giới hạn đàn hồi là mức độ biến dạng tối đa mà lò xo có thể chịu được mà vẫn có thể trở về trạng thái ban đầu sau khi không còn tác động của lực bên ngoài.
Lực đàn hồi của lò xo đóng vai trò quan trọng trong nhiều ứng dụng thực tế, từ các thiết bị đơn giản như bút bi, cân lò xo cho đến các hệ thống phức tạp hơn như hệ thống treo xe hơi, thiết bị tập luyện thể thao và trong ngành y tế. Sự hiểu biết về lực đàn hồi và các yếu tố ảnh hưởng đến nó giúp con người có thể thiết kế và sử dụng các thiết bị một cách hiệu quả và an toàn.
2. Định luật Hooke và công thức tính lực đàn hồi
Định luật Hooke là một trong những định luật cơ bản của cơ học, đặc biệt quan trọng trong việc nghiên cứu và ứng dụng tính đàn hồi của các vật liệu như lò xo. Theo định luật này, lực đàn hồi \( F \) của một lò xo tỷ lệ thuận với độ biến dạng của nó \( \Delta x \), được biểu diễn bằng công thức:
\( F = k \cdot \Delta x \)
- \( F \): Lực đàn hồi (đơn vị: Newton, \( N \)).
- \( k \): Hằng số đàn hồi của lò xo (đơn vị: Newton trên mét, \( N/m \)).
- \( \Delta x \): Độ biến dạng của lò xo so với chiều dài tự nhiên (đơn vị: mét, \( m \)).
Công thức trên cho phép tính toán lực đàn hồi khi lò xo bị nén hoặc kéo dãn. Hằng số đàn hồi \( k \) là một đặc tính cố định của lò xo và phụ thuộc vào chất liệu cũng như thiết kế của nó. Để tính toán lực đàn hồi chính xác, bạn cần biết giá trị \( k \) và độ biến dạng \( \Delta x \).
Định luật Hooke không chỉ áp dụng cho lò xo mà còn cho nhiều vật liệu khác có tính đàn hồi, chẳng hạn như dây cao su hay thanh kim loại bị uốn cong. Tuy nhiên, định luật này chỉ đúng trong giới hạn đàn hồi của vật liệu, tức là khi vật liệu không bị biến dạng vĩnh viễn.
| Đại Lượng | Ký Hiệu | Đơn Vị | Mô Tả |
|---|---|---|---|
| Lực Đàn Hồi | \( F \) | Newton (N) | Lực sinh ra để chống lại sự biến dạng |
| Hằng Số Đàn Hồi | \( k \) | Newton trên mét (N/m) | Độ cứng của vật liệu đàn hồi |
| Độ Biến Dạng | \( \Delta x \) | Mét (m) | Độ thay đổi chiều dài so với trạng thái ban đầu |
Ví dụ: Giả sử một lò xo có hằng số đàn hồi \( k = 100 \, N/m \). Nếu lò xo này bị kéo dãn thêm 0.1m so với chiều dài ban đầu, lực đàn hồi sinh ra sẽ là:
\( F = 100 \, N/m \times 0.1 \, m = 10 \, N \)
Như vậy, lực đàn hồi của lò xo trong trường hợp này là 10N, ngược chiều với lực kéo và có xu hướng đưa lò xo về trạng thái ban đầu.

3. Các thí nghiệm về lực đàn hồi của lò xo
Thí nghiệm về lực đàn hồi của lò xo là một trong những thí nghiệm cơ bản trong vật lý để hiểu rõ hơn về định luật Hooke. Dưới đây là các bước thực hiện thí nghiệm để xác định hệ số đàn hồi (k) của lò xo và kiểm chứng công thức tính lực đàn hồi:
- Mục đích: Xác định hệ số đàn hồi (k) của lò xo và kiểm chứng định luật Hooke.
- Thiết bị thí nghiệm:
- Một lò xo
- Bộ giá treo
- Các quả cân có khối lượng khác nhau
- Thước đo chiều dài
- Cân điện tử
- Các bước thực hiện:
- Treo lò xo vào giá đỡ và đo chiều dài tự nhiên của lò xo \( l_0 \).
- Gắn một quả cân có khối lượng \( m \) vào lò xo và để lò xo đạt trạng thái cân bằng.
- Đo chiều dài của lò xo sau khi treo quả cân \( l \).
- Tính độ biến dạng của lò xo: \( \Delta l = l - l_0 \).
- Tính lực đàn hồi: \( F_{dh} = m \cdot g \), trong đó \( g \approx 9.8 \, \text{m/s}^2 \).
- Lặp lại các bước trên với các quả cân khác nhau và ghi lại kết quả.
- Phân tích kết quả:
- Bảng kết quả thí nghiệm:
Sử dụng các dữ liệu thu thập được, ta có thể xác định hệ số đàn hồi \( k \) của lò xo bằng cách sử dụng công thức định luật Hooke:
\[
F_{dh} = k \cdot \Delta l
\]
Với \( k \) được tính theo phương trình:
\[
k = \frac{F_{dh}}{\Delta l}
\]
| Khối lượng (kg) | Chiều dài ban đầu (m) | Chiều dài sau khi treo (m) | Độ biến dạng (m) | Lực đàn hồi (N) | Hệ số đàn hồi (N/m) |
| 0.1 | 0.2 | 0.3 | 0.1 | 0.98 | 9.8 |
| 0.2 | 0.2 | 0.4 | 0.2 | 1.96 | 9.8 |

XEM THÊM:
4. Ứng dụng của lực đàn hồi trong cuộc sống
Lực đàn hồi, đặc biệt là lực đàn hồi của lò xo, có nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Nhờ vào tính chất có thể thay đổi độ dài khi chịu lực tác động và sau đó trở về trạng thái ban đầu, lò xo được sử dụng rộng rãi trong nhiều lĩnh vực.
- Hệ thống treo của xe cộ: Trong các phương tiện giao thông như xe hơi, xe đạp, hay xe máy, lò xo là một phần quan trọng của hệ thống treo. Nó giúp giảm sốc, làm êm ái khi di chuyển trên địa hình không bằng phẳng.
- Đồng hồ cơ: Lực đàn hồi của lò xo là cơ chế chính trong việc điều chỉnh và duy trì hoạt động của đồng hồ cơ, giúp chúng hoạt động chính xác và đều đặn theo thời gian.
- Ghế xoay và ghế ngồi: Các loại ghế văn phòng, ghế xoay đều sử dụng lò xo để điều chỉnh chiều cao, tạo sự thoải mái khi ngồi và dễ dàng di chuyển.
- Các thiết bị thể thao: Lực đàn hồi của lò xo được ứng dụng trong các dụng cụ thể thao như máy chạy bộ, thiết bị tập gym để cung cấp lực cản và hỗ trợ người tập luyện.
- Đồ chơi trẻ em: Lò xo còn được dùng trong nhiều loại đồ chơi như súng lò xo, xe lò xo, mang lại tính năng đàn hồi, tạo cảm giác vui vẻ cho trẻ em khi chơi.
Nhìn chung, lực đàn hồi và các ứng dụng của nó đóng vai trò quan trọng trong việc nâng cao chất lượng cuộc sống, từ những thiết bị nhỏ nhất như đồng hồ đến các hệ thống phức tạp như hệ thống treo của xe cộ.

5. Các bài tập và ví dụ minh họa
Dưới đây là một số bài tập và ví dụ minh họa liên quan đến lực đàn hồi của lò xo, giúp bạn hiểu rõ hơn về cách tính toán và áp dụng định luật Hooke trong thực tế.
- Bài tập 1: Một lò xo có độ cứng k = 200 N/m và chiều dài tự nhiên là 20 cm. Khi treo một vật có khối lượng 1,5 kg, lò xo dãn ra bao nhiêu? Tính lực đàn hồi của lò xo trong trường hợp này.
- Sử dụng công thức định luật Hooke: \( F_{đh} = k \cdot \Delta l \) và \( F_{đh} = mg \).
- Áp dụng \( k = 200 \, N/m \), \( m = 1,5 \, kg \) và \( g = 10 \, m/s^2 \), ta có:
- Độ dãn của lò xo \( \Delta l = \frac{mg}{k} = \frac{1,5 \cdot 10}{200} = 0,075 \, m = 7,5 \, cm \).
- Lực đàn hồi của lò xo là \( F_{đh} = 15 \, N \).
- Bài tập 2: Một lò xo có độ cứng \( k = 50 \, N/m \) bị cắt thành hai lò xo có độ dài lần lượt là 20 cm và 10 cm. Tính độ cứng của từng lò xo sau khi cắt.
- Sử dụng công thức \( k \cdot l_0 = k_1 \cdot l_1 = k_2 \cdot l_2 \).
- Áp dụng \( k = 50 \, N/m \), \( l_0 = 30 \, cm \), \( l_1 = 20 \, cm \), \( l_2 = 10 \, cm \), ta có:
- Độ cứng của lò xo thứ nhất \( k_1 = \frac{k \cdot l_0}{l_1} = \frac{50 \cdot 30}{20} = 75 \, N/m \).
- Độ cứng của lò xo thứ hai \( k_2 = \frac{k \cdot l_0}{l_2} = \frac{50 \cdot 30}{10} = 150 \, N/m \).
- Bài tập 3: Một lò xo có chiều dài tự nhiên 30 cm, khi treo vật nặng 200g vào, lò xo dãn ra 4 cm. Tính lực đàn hồi của lò xo.
- Vật treo có khối lượng \( m = 0,2 \, kg \), \( g = 10 \, m/s^2 \).
- Lực đàn hồi \( F_{đh} = mg = 0,2 \cdot 10 = 2 \, N \).
- Độ dãn của lò xo \( \Delta l = 4 \, cm = 0,04 \, m \).
- Suy ra độ cứng của lò xo \( k = \frac{F_{đh}}{\Delta l} = \frac{2}{0,04} = 50 \, N/m \).
Lời giải:
Lời giải:
Lời giải:
6. Kết luận
Trong vật lý, lực đàn hồi của lò xo là một khái niệm cơ bản nhưng có ý nghĩa quan trọng cả trong học tập lẫn ứng dụng thực tiễn. Hiểu rõ về định luật Hooke, công thức tính lực đàn hồi và các yếu tố liên quan như độ cứng của lò xo và độ biến dạng sẽ giúp chúng ta áp dụng một cách hiệu quả trong các lĩnh vực khác nhau.
Từ các thí nghiệm đo lường, việc xác định giới hạn đàn hồi cho đến những ứng dụng đa dạng trong đời sống như trong các thiết bị giảm chấn, cân đo lường, và các hệ thống treo, lực đàn hồi luôn hiện diện và đóng vai trò then chốt. Chính vì vậy, việc nắm vững kiến thức này không chỉ giúp học sinh, sinh viên giải quyết tốt các bài toán vật lý mà còn là nền tảng để phát triển các công nghệ và ứng dụng mới trong tương lai.
Nhìn chung, hiểu biết sâu sắc về lực đàn hồi không chỉ là một yêu cầu trong giáo dục mà còn là tiền đề để thúc đẩy sự sáng tạo và cải tiến trong các ngành công nghiệp. Với sự tiến bộ của khoa học kỹ thuật, việc nghiên cứu và áp dụng lực đàn hồi sẽ còn tiếp tục mở ra nhiều hướng đi mới, góp phần nâng cao chất lượng cuộc sống.