Chủ đề cường độ điện trường là đại lượng đặc trưng cho: Cường độ điện trường là đại lượng đặc trưng cho khả năng tác động của lực điện lên các điện tích trong không gian. Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản và ứng dụng thực tế về cường độ điện trường, giúp bạn hiểu rõ hơn về vai trò và tầm quan trọng của nó trong vật lý và đời sống.
Mục lục
- Cường độ điện trường là đại lượng đặc trưng cho
- 1. Khái niệm và định nghĩa về cường độ điện trường
- 2. Đơn vị đo và ký hiệu của cường độ điện trường
- 3. Cách tính và biểu thức của cường độ điện trường
- 4. Các yếu tố ảnh hưởng đến cường độ điện trường
- 5. Các ứng dụng thực tế của cường độ điện trường
- 6. So sánh cường độ điện trường và các đại lượng liên quan
- 7. Những điều cần lưu ý khi tính toán cường độ điện trường
- 8. Kết luận về vai trò của cường độ điện trường trong vật lý
Cường độ điện trường là đại lượng đặc trưng cho
Cường độ điện trường là một khái niệm quan trọng trong vật lý, được sử dụng để đo lường độ mạnh yếu của điện trường tại một điểm cụ thể. Nó thể hiện khả năng tác dụng lực của điện trường lên các điện tích thử đặt tại điểm đó. Công thức để tính cường độ điện trường được biểu diễn dưới dạng:
\[ E = \frac{F}{q} \]
Trong đó:
- E: Cường độ điện trường (đơn vị: V/m hoặc N/C)
- F: Lực điện tác dụng lên điện tích thử (đơn vị: Newton, N)
- q: Điện tích thử tại điểm xét (đơn vị: Coulomb, C)
Khái niệm và ứng dụng của cường độ điện trường
Cường độ điện trường tại một điểm được định nghĩa là thương số giữa lực điện tác dụng lên điện tích thử tại điểm đó và độ lớn của điện tích thử. Cường độ điện trường phản ánh sự phân bố và cường độ của điện trường trong không gian, từ đó có thể dự đoán được tác động của điện trường lên các vật mang điện trong môi trường xung quanh.
Cường độ điện trường còn được biểu diễn bằng vectơ, có phương và chiều trùng với lực điện tác dụng lên điện tích thử dương tại điểm xét. Vectơ cường độ điện trường có độ dài tỉ lệ với độ lớn của cường độ điện trường.
Các yếu tố ảnh hưởng đến cường độ điện trường
- Điện tích nguồn: Nguồn tạo ra điện trường có thể là một điện tích điểm, một dòng điện, hoặc từ trường biến đổi. Điện tích nguồn càng lớn, cường độ điện trường càng mạnh.
- Khoảng cách: Cường độ điện trường tại một điểm tỉ lệ nghịch với bình phương khoảng cách từ nguồn đến điểm đó. Càng xa nguồn, cường độ điện trường càng giảm.
- Môi trường xung quanh: Môi trường xung quanh có thể làm tăng hoặc giảm cường độ điện trường tùy thuộc vào tính chất dẫn điện của vật liệu trong môi trường đó.
Ứng dụng của cường độ điện trường
Cường độ điện trường có nhiều ứng dụng trong đời sống và công nghệ, chẳng hạn như trong thiết kế tụ điện, đo lượng sóng điện từ từ các thiết bị di động, và các ứng dụng liên quan đến điện lực.
Một ví dụ về công thức tính cường độ điện trường trong trường hợp một điện tích điểm trong chân không là:
\[ E = k \cdot \frac{|Q|}{r^2} \]
Trong đó:
- k: Hằng số điện môi (khoảng 8.99 × 10^9 N·m²/C²)
- Q: Điện tích của nguồn tạo ra điện trường (đơn vị: C)
- r: Khoảng cách từ nguồn đến điểm xét (đơn vị: m)

.png)
1. Khái niệm và định nghĩa về cường độ điện trường
Cường độ điện trường là một đại lượng vật lý quan trọng trong điện từ học, đặc trưng cho khả năng tác động của lực điện lên các điện tích trong không gian. Đại lượng này được xác định thông qua lực mà một điện tích thử \( q \) chịu tác động khi nó nằm trong một điện trường.
Khái niệm này có thể được biểu diễn thông qua công thức:
\[
\mathbf{E} = \frac{\mathbf{F}}{q}
\]
Trong đó:
- \(\mathbf{E}\): Cường độ điện trường (đơn vị V/m hoặc N/C)
- \(\mathbf{F}\): Lực điện tác dụng lên điện tích thử (đơn vị N)
- \(q\): Điện tích thử (đơn vị C)
Cường độ điện trường là một vector có phương và chiều, trong đó:
- Phương: Trùng với phương của lực điện tác dụng lên điện tích thử.
- Chiều: Nếu điện tích thử là dương, cường độ điện trường sẽ cùng chiều với lực. Nếu điện tích thử là âm, cường độ điện trường sẽ ngược chiều với lực.
Một điện trường được coi là mạnh hay yếu phụ thuộc vào giá trị của cường độ điện trường. Cường độ điện trường càng lớn thì lực tác dụng lên điện tích thử càng mạnh.
Bên cạnh đó, ta cũng có thể biểu diễn cường độ điện trường thông qua điện thế bằng công thức:
\[
\mathbf{E} = - \nabla V
\]
Trong đó:
- \(V\): Điện thế tại một điểm trong điện trường (đơn vị V)
- \(\nabla V\): Độ dốc của điện thế theo không gian.
Như vậy, cường độ điện trường không chỉ phụ thuộc vào lực và điện tích, mà còn có thể được mô tả dựa trên sự thay đổi điện thế trong không gian. Điều này tạo nên nền tảng cho nhiều ứng dụng quan trọng trong các lĩnh vực công nghệ và đời sống.
2. Đơn vị đo và ký hiệu của cường độ điện trường
Cường độ điện trường là một đại lượng vector trong vật lý, có đơn vị đo và ký hiệu cụ thể. Hiểu rõ đơn vị và ký hiệu của cường độ điện trường là bước quan trọng để giải quyết các bài toán liên quan đến điện từ trường.
2.1. Đơn vị đo của cường độ điện trường
Đơn vị đo của cường độ điện trường trong hệ SI là Vôn trên mét (V/m) hoặc Newton trên Coulomb (N/C). Hai đơn vị này có mối quan hệ tương đương với nhau.
Công thức xác định cường độ điện trường:
\[
\mathbf{E} = \frac{\mathbf{F}}{q} = \frac{\text{Newton}}{\text{Coulomb}} = \frac{\text{Vôn}}{\text{Mét}}
\]
Như vậy, có thể sử dụng cả hai cách viết \( V/m \) hoặc \( N/C \) để biểu diễn cường độ điện trường, tùy thuộc vào ngữ cảnh bài toán.
2.2. Ký hiệu của cường độ điện trường
Trong các tài liệu khoa học và kỹ thuật, cường độ điện trường thường được ký hiệu bằng chữ cái hoa \( \mathbf{E} \). Đây là một vector có phương và chiều cụ thể. Điểm đặc trưng của vector cường độ điện trường là hướng của nó chỉ theo hướng lực điện tác động lên một điện tích dương đặt trong điện trường.
2.3. Bảng tóm tắt các đơn vị và ký hiệu
| Đại lượng | Ký hiệu | Đơn vị | Đơn vị SI |
|---|---|---|---|
| Cường độ điện trường | \( \mathbf{E} \) | Vôn trên mét | V/m |
| Cường độ điện trường | \( \mathbf{E} \) | Newton trên Coulomb | N/C |
Như vậy, cường độ điện trường có hai cách biểu diễn về đơn vị nhưng cùng ý nghĩa về mặt vật lý. Ký hiệu \( \mathbf{E} \) là một tiêu chuẩn quốc tế trong các bài toán điện trường.

3. Cách tính và biểu thức của cường độ điện trường
Cường độ điện trường là một đại lượng vector, biểu diễn mức độ tác động của lực điện lên một điện tích trong không gian. Để tính toán cường độ điện trường, chúng ta cần hiểu các công thức cơ bản và các yếu tố ảnh hưởng đến nó. Dưới đây là những cách tính phổ biến nhất.
3.1. Biểu thức tổng quát của cường độ điện trường
Biểu thức tổng quát của cường độ điện trường tại một điểm trong không gian được xác định bằng công thức:
\[
\mathbf{E} = \frac{\mathbf{F}}{q}
\]
Trong đó:
- \(\mathbf{E}\): Cường độ điện trường (V/m hoặc N/C)
- \(\mathbf{F}\): Lực điện tác dụng lên điện tích thử (N)
- \(q\): Điện tích thử (C)
Công thức này cho biết cường độ điện trường phụ thuộc trực tiếp vào lực điện mà một điện tích thử phải chịu tại một điểm trong điện trường và tỷ lệ thuận với giá trị lực điện.
3.2. Cách tính cường độ điện trường do một điện tích điểm sinh ra
Cường độ điện trường do một điện tích điểm \(Q\) sinh ra tại một khoảng cách \(r\) trong chân không được tính bằng công thức:
\[
\mathbf{E} = k \cdot \frac{|Q|}{r^2}
\]
Trong đó:
- \(k\): Hằng số điện trường Coulomb, \(k \approx 9 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2\)
- \(Q\): Điện tích gây ra điện trường (C)
- \(r\): Khoảng cách từ điện tích \(Q\) đến điểm tính cường độ điện trường (m)
Công thức này cho thấy cường độ điện trường giảm nhanh chóng theo khoảng cách \(r\), và phụ thuộc vào giá trị của điện tích \(Q\).
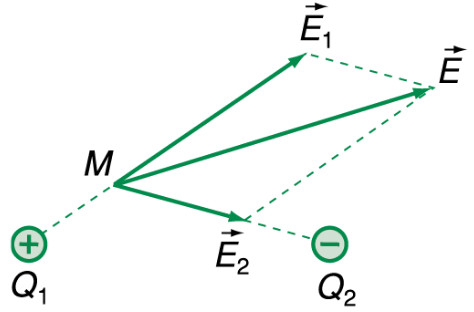
3.3. Cách tính cường độ điện trường do nhiều điện tích điểm sinh ra
Khi có nhiều điện tích điểm, cường độ điện trường tổng tại một điểm được tính bằng cách cộng vector của các cường độ điện trường do từng điện tích gây ra. Công thức tổng quát là:
\[
\mathbf{E}_{\text{tổng}} = \sum_{i=1}^{n} \mathbf{E}_i
\]
Trong đó:
- \(\mathbf{E}_i\): Cường độ điện trường do điện tích \(Q_i\) sinh ra
- \(n\): Số lượng các điện tích
Các cường độ điện trường này sẽ được cộng vector, nghĩa là chúng phải được tính toán theo cả phương và chiều của từng điện tích trước khi cộng lại.
3.4. Ví dụ minh họa
Giả sử chúng ta có một điện tích điểm \(Q = 1 \, \text{C}\), đặt cách điểm cần tính cường độ điện trường một khoảng \(r = 2 \, \text{m}\). Cường độ điện trường tại điểm đó sẽ được tính như sau:
\[
\mathbf{E} = 9 \times 10^9 \cdot \frac{1}{2^2} = 2.25 \times 10^9 \, \text{V/m}
\]
Như vậy, cường độ điện trường tại điểm cách điện tích \(Q\) một khoảng 2 mét là \(2.25 \times 10^9 \, \text{V/m}\).
Các bước tính toán cường độ điện trường cần được thực hiện cẩn thận để đảm bảo độ chính xác, đặc biệt khi cộng các vector cường độ từ nhiều nguồn khác nhau.

XEM THÊM:
4. Các yếu tố ảnh hưởng đến cường độ điện trường
Cường độ điện trường là một đại lượng có thể thay đổi tùy theo nhiều yếu tố khác nhau. Hiểu rõ các yếu tố này giúp chúng ta xác định chính xác hơn giá trị của cường độ điện trường trong các tình huống thực tế.
4.1. Điện tích nguồn
Cường độ điện trường phụ thuộc trực tiếp vào giá trị của điện tích nguồn. Nếu điện tích \( Q \) tăng, cường độ điện trường cũng tăng theo. Biểu thức cho cường độ điện trường do một điện tích điểm sinh ra:
\[
\mathbf{E} = k \cdot \frac{|Q|}{r^2}
\]
Điều này có nghĩa là cường độ điện trường tỷ lệ thuận với điện tích nguồn \( Q \). Khi \( Q \) tăng, lực điện tác dụng lên các điện tích thử cũng tăng, dẫn đến cường độ điện trường lớn hơn.
4.2. Khoảng cách từ điện tích đến điểm xét
Khoảng cách \( r \) từ điện tích nguồn đến điểm xét trong điện trường cũng có ảnh hưởng lớn đến cường độ điện trường. Công thức trên cho thấy cường độ điện trường tỷ lệ nghịch với bình phương của khoảng cách:
\[
\mathbf{E} \propto \frac{1}{r^2}
\]
Điều này có nghĩa là khi khoảng cách tăng lên, cường độ điện trường sẽ giảm nhanh chóng. Ngược lại, khi khoảng cách giảm, cường độ điện trường sẽ tăng mạnh.
4.3. Môi trường xung quanh
Môi trường mà điện tích được đặt vào cũng ảnh hưởng đến cường độ điện trường. Trong môi trường có hằng số điện môi \( \varepsilon \) khác với hằng số của chân không \( \varepsilon_0 \), cường độ điện trường sẽ thay đổi theo công thức:
\[
\mathbf{E} = \frac{k \cdot |Q|}{\varepsilon \cdot r^2}
\]
Ở đây, \( \varepsilon \) là hằng số điện môi của môi trường. Nếu môi trường có tính chất cách điện cao, như không khí, nước, hoặc dầu, cường độ điện trường sẽ yếu hơn so với trong chân không.
4.4. Phân bố điện tích
Phân bố của điện tích cũng ảnh hưởng đến cường độ điện trường. Với các vật có phân bố điện tích khác nhau (điện tích điểm, điện tích phân bố đều trên đường thẳng, bề mặt hoặc trong thể tích), cường độ điện trường sẽ có cách tính toán khác nhau.
Ví dụ, đối với điện tích phân bố đều trên một quả cầu dẫn điện, cường độ điện trường bên ngoài quả cầu được tính như sau:
\[
\mathbf{E} = k \cdot \frac{Q}{r^2} \quad \text{(ngoài quả cầu)}
\]
Trong khi đó, cường độ điện trường bên trong quả cầu là bằng không:
\[
\mathbf{E} = 0 \quad \text{(bên trong quả cầu)}
\]
4.5. Sự tác động của các điện trường khác
Khi có nhiều nguồn điện trường tác động lẫn nhau, cường độ điện trường tại một điểm sẽ là tổng hợp của các cường độ điện trường do từng nguồn gây ra. Sự cộng hưởng này có thể làm tăng hoặc giảm giá trị của cường độ điện trường tổng tại một điểm nhất định.
Do đó, khi tính toán cường độ điện trường tổng, ta phải xét đến sự đóng góp của tất cả các điện trường hiện diện.
Như vậy, các yếu tố như điện tích nguồn, khoảng cách, môi trường, phân bố điện tích và sự tác động của các điện trường khác đều ảnh hưởng trực tiếp đến cường độ điện trường. Việc nắm vững các yếu tố này giúp chúng ta có thể dự đoán và tính toán chính xác hơn trong các tình huống thực tế.

5. Các ứng dụng thực tế của cường độ điện trường
Cường độ điện trường không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và kỹ thuật. Từ các công nghệ hiện đại đến các thiết bị hàng ngày, việc hiểu rõ cường độ điện trường giúp con người tạo ra và cải tiến nhiều sản phẩm, dịch vụ.
5.1. Ứng dụng trong công nghệ cảm biến
Cường độ điện trường được sử dụng rộng rãi trong các cảm biến điện dung và cảm biến điện trường. Những cảm biến này hoạt động dựa trên sự thay đổi của cường độ điện trường khi có vật thể di chuyển gần hoặc tiếp xúc với bề mặt cảm biến. Điều này được ứng dụng trong:
- Cảm biến tiệm cận trên điện thoại thông minh.
- Cảm biến nhận diện cử chỉ không chạm trong các thiết bị thông minh.
- Hệ thống an ninh phát hiện người xâm nhập.
5.2. Ứng dụng trong y tế
Cường độ điện trường cũng đóng vai trò quan trọng trong các thiết bị y tế, như máy chụp cộng hưởng từ (MRI). Trong quá trình MRI, cường độ điện trường mạnh được tạo ra để tác động lên cơ thể, giúp tạo ra hình ảnh chi tiết bên trong mà không cần xâm lấn. Ngoài ra, điện trường còn được sử dụng trong các phương pháp điều trị bằng điện, giúp kích thích các dây thần kinh và cơ bắp.
5.3. Ứng dụng trong truyền thông và sóng vô tuyến
Cường độ điện trường có vai trò quan trọng trong việc phát và nhận sóng vô tuyến. Các trạm phát sóng truyền tín hiệu thông qua điện trường và từ trường biến đổi, từ đó truyền tín hiệu qua không gian. Ứng dụng này rất phổ biến trong các lĩnh vực như:
- Truyền hình và phát thanh.
- Hệ thống thông tin di động (4G, 5G).
- Wi-Fi và các thiết bị không dây.
5.4. Ứng dụng trong các thiết bị điện và điện tử
Cường độ điện trường được sử dụng để tính toán và thiết kế các mạch điện và linh kiện điện tử, chẳng hạn như tụ điện. Tụ điện lưu trữ năng lượng điện bằng cách tạo ra một điện trường giữa hai bản cực. Những linh kiện này có mặt trong hầu hết các thiết bị điện tử từ máy tính, điện thoại đến TV.
5.5. Ứng dụng trong công nghiệp năng lượng
Trong công nghiệp năng lượng, cường độ điện trường được ứng dụng để thiết kế các hệ thống truyền tải điện cao áp. Các kỹ sư sử dụng các công thức về cường độ điện trường để đảm bảo an toàn cho các trạm biến áp, đường dây điện và các thiết bị khác. Việc kiểm soát cường độ điện trường giúp giảm thiểu tổn thất năng lượng trong quá trình truyền tải.
5.6. Ứng dụng trong nghiên cứu khoa học
Cường độ điện trường là một trong những yếu tố chính trong nhiều nghiên cứu khoa học, đặc biệt là trong vật lý hạt và vật lý plasma. Các nhà khoa học sử dụng điện trường mạnh để nghiên cứu các hạt cơ bản, cũng như điều khiển plasma trong các phản ứng nhiệt hạch. Những nghiên cứu này có tiềm năng lớn trong việc phát triển nguồn năng lượng sạch trong tương lai.
Như vậy, cường độ điện trường có vô số ứng dụng trong đời sống, từ những công nghệ thông minh hiện đại đến các thiết bị y tế, nghiên cứu khoa học và công nghiệp. Việc hiểu rõ và ứng dụng cường độ điện trường giúp thúc đẩy sự tiến bộ và phát triển của công nghệ và khoa học kỹ thuật.
6. So sánh cường độ điện trường và các đại lượng liên quan
Cường độ điện trường là một trong những đại lượng cơ bản trong điện học, nhưng để hiểu rõ hơn về ý nghĩa của nó, chúng ta cần so sánh với các đại lượng liên quan khác như điện thế, lực điện và mật độ điện tích. Việc so sánh này giúp làm sáng tỏ mối quan hệ giữa chúng và cách chúng ảnh hưởng lẫn nhau trong các bài toán vật lý.
6.1. So sánh giữa cường độ điện trường và điện thế
Điện thế \( V \) và cường độ điện trường \( \mathbf{E} \) có mối quan hệ mật thiết với nhau. Điện thế biểu thị mức năng lượng trên một đơn vị điện tích, trong khi cường độ điện trường đo lường lực tác dụng lên điện tích đó.
Mối quan hệ giữa chúng được thể hiện qua công thức:
\[
\mathbf{E} = - \nabla V
\]
Điều này có nghĩa là cường độ điện trường là đạo hàm của điện thế theo không gian, tức là sự thay đổi của điện thế sẽ dẫn đến sự thay đổi của cường độ điện trường. Trong không gian có điện thế không đổi, cường độ điện trường bằng 0.
6.2. So sánh giữa cường độ điện trường và lực điện
Cường độ điện trường và lực điện \( \mathbf{F} \) có mối liên hệ trực tiếp thông qua công thức:
\[
\mathbf{F} = q \cdot \mathbf{E}
\]
Ở đây, \( q \) là điện tích của vật chịu tác động. Lực điện là kết quả của tác động của cường độ điện trường lên điện tích. Điều này có nghĩa là khi cường độ điện trường tăng, lực điện tác dụng lên một điện tích nhất định cũng tăng.
6.3. So sánh giữa cường độ điện trường và mật độ điện tích
Mật độ điện tích \( \rho \) biểu thị số lượng điện tích trên một đơn vị thể tích. Mối quan hệ giữa mật độ điện tích và cường độ điện trường được xác định bởi định lý Gauss:
\[
\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}
\]
Trong đó, \( \varepsilon_0 \) là hằng số điện môi của chân không. Công thức này cho thấy cường độ điện trường tại một điểm có thể được tạo ra bởi sự phân bố mật độ điện tích xung quanh điểm đó. Nếu mật độ điện tích lớn, cường độ điện trường tại vị trí gần đó cũng sẽ lớn.
6.4. So sánh giữa cường độ điện trường và điện thông
Điện thông \( \Phi_E \) là đại lượng đo lượng cường độ điện trường xuyên qua một bề mặt kín. Mối quan hệ giữa điện thông và cường độ điện trường được định nghĩa bởi định lý Gauss:
\[
\Phi_E = \oint \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{bao}}}{\varepsilon_0}
\]
Trong đó, \( Q_{\text{bao}} \) là tổng điện tích được bao quanh bởi bề mặt. Như vậy, điện thông phụ thuộc vào cường độ điện trường và diện tích bề mặt. Khi cường độ điện trường tăng, điện thông xuyên qua bề mặt cũng tăng lên.
6.5. Bảng so sánh các đại lượng liên quan
| Đại lượng | Ký hiệu | Mối quan hệ với cường độ điện trường |
|---|---|---|
| Điện thế | \( V \) | \( \mathbf{E} = - \nabla V \) |
| Lực điện | \( \mathbf{F} \) | \( \mathbf{F} = q \cdot \mathbf{E} \) |
| Mật độ điện tích | \( \rho \) | \( \nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0} \) |
| Điện thông | \( \Phi_E \) | \( \Phi_E = \oint \mathbf{E} \cdot d\mathbf{A} \) |
Qua bảng so sánh trên, chúng ta thấy rằng cường độ điện trường không chỉ là một đại lượng độc lập mà còn liên quan mật thiết đến nhiều đại lượng khác trong điện học. Hiểu được mối liên hệ này giúp ta giải quyết các bài toán điện học một cách toàn diện và chính xác hơn.

7. Những điều cần lưu ý khi tính toán cường độ điện trường
Việc tính toán cường độ điện trường đòi hỏi sự chính xác và cẩn thận để đảm bảo kết quả đúng đắn. Dưới đây là những điều quan trọng cần lưu ý khi thực hiện các bài toán liên quan đến cường độ điện trường.
7.1. Xác định đúng loại nguồn điện trường
Đầu tiên, cần xác định rõ loại nguồn tạo ra điện trường. Có hai loại nguồn chính:
- Điện tích điểm: Đối với điện tích điểm, cường độ điện trường \( E \) được tính theo công thức: \[ E = \frac{k \cdot |q|}{r^2} \] Trong đó, \( k \) là hằng số điện, \( q \) là điện tích và \( r \) là khoảng cách từ điểm đang xét đến nguồn điện tích.
- Dòng điện hoặc hệ thống dây dẫn: Đối với các trường hợp có dây dẫn hoặc dòng điện, cường độ điện trường được xác định dựa trên các tích phân phức tạp hoặc ứng dụng của định lý Gauss.
7.2. Xem xét hình học và phân bố điện tích
Khi tính toán cường độ điện trường, hình học của hệ thống và cách điện tích được phân bố là yếu tố then chốt. Ví dụ, với điện tích phân bố đều trên mặt cầu, cường độ điện trường bên ngoài mặt cầu được tính như đối với một điện tích điểm. Trong khi đó, bên trong mặt cầu, cường độ điện trường bằng 0.
7.3. Ứng dụng định lý Gauss
Định lý Gauss là một công cụ mạnh mẽ giúp đơn giản hóa việc tính toán cường độ điện trường trong các hệ thống đối xứng cao như mặt cầu, mặt trụ hoặc mặt phẳng vô tận. Công thức định lý Gauss được viết dưới dạng:
\[
\Phi_E = \oint \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{bao}}}{\varepsilon_0}
\]
Trong các hệ đối xứng, sử dụng định lý Gauss giúp rút gọn bài toán tính cường độ điện trường chỉ còn phụ thuộc vào hình dạng của mặt kín và điện tích bao quanh.
7.4. Đơn vị đo và hệ số điện môi
Luôn đảm bảo rằng các đơn vị đo trong các công thức phù hợp với nhau. Đơn vị của cường độ điện trường là V/m (vôn trên mét). Hơn nữa, cần lưu ý hệ số điện môi \( \varepsilon_0 \) đối với các môi trường khác nhau (chẳng hạn, chân không có giá trị khác với các vật liệu khác).
7.5. Xem xét các tương tác với từ trường
Trong các bài toán có sự hiện diện đồng thời của từ trường, việc tính toán cần xét đến tương tác giữa điện trường và từ trường. Trong những trường hợp này, việc sử dụng các phương trình Maxwell có thể cần thiết để giải quyết.
7.6. Các yếu tố ngoại cảnh và điều kiện biên
Khi tính toán cường độ điện trường, cần chú ý đến các yếu tố ngoại cảnh và điều kiện biên. Các yếu tố này bao gồm:
- Điều kiện môi trường: Môi trường có tính dẫn điện hay cách điện sẽ ảnh hưởng đến cách điện trường lan truyền.
- Điều kiện biên: Cần phải xem xét điều kiện biên của bài toán, chẳng hạn như sự hiện diện của các vật cách điện hoặc dẫn điện xung quanh nguồn điện trường.
7.7. Kiểm tra kết quả với các trường hợp đặc biệt
Sau khi tính toán, một cách kiểm tra hiệu quả là so sánh kết quả với các trường hợp đặc biệt mà ta đã biết đáp án trước đó. Điều này giúp xác minh tính chính xác của phương pháp và kết quả đã tìm được.
Những lưu ý trên giúp bạn tự tin hơn khi thực hiện các bài toán liên quan đến cường độ điện trường, từ việc xác định nguồn điện trường đến ứng dụng các định lý và kiểm tra kết quả cuối cùng.

8. Kết luận về vai trò của cường độ điện trường trong vật lý
Cường độ điện trường đóng vai trò quan trọng và cơ bản trong vật lý, đặc biệt trong việc hiểu rõ các hiện tượng liên quan đến lực điện và tương tác điện từ. Nó không chỉ là một đại lượng đo lường mà còn cung cấp cách tiếp cận để tính toán và dự đoán các tương tác điện trong nhiều hệ thống khác nhau. Dưới đây là những kết luận chính về vai trò của cường độ điện trường trong vật lý.
8.1. Cường độ điện trường và lực điện
Cường độ điện trường \(\mathbf{E}\) giúp mô tả sự phân bố của điện trường trong không gian và là yếu tố quan trọng trong việc xác định lực tác dụng lên các điện tích trong trường đó. Lực điện tác dụng lên điện tích \(q\) được tính thông qua công thức:
\[
\mathbf{F} = q \cdot \mathbf{E}
\]
Điều này giúp chúng ta hiểu rõ hơn về cách các hạt điện tích tương tác với nhau và với môi trường xung quanh.
8.2. Ứng dụng trong điện động lực học
Cường độ điện trường là một thành phần chính trong điện động lực học, đóng vai trò quan trọng trong mô tả sự lan truyền của sóng điện từ. Nó là một trong những đại lượng kết hợp với từ trường để tạo ra các phương trình Maxwell, là nền tảng của lý thuyết trường điện từ.
8.3. Định lý Gauss và sự đối xứng
Cường độ điện trường là công cụ hữu hiệu trong việc sử dụng định lý Gauss để tính toán điện trường trong các hệ thống đối xứng, như mặt cầu hoặc trụ. Điều này giúp giảm thiểu độ phức tạp của các bài toán và đưa ra kết quả nhanh chóng, chính xác.
8.4. Vai trò trong các ngành công nghệ
Trong thực tế, cường độ điện trường có nhiều ứng dụng quan trọng trong các ngành công nghệ như thiết kế mạch điện, hệ thống truyền tải điện, và công nghệ viễn thông. Cường độ điện trường giúp tối ưu hóa các thiết bị điện và nâng cao hiệu suất của các hệ thống công nghệ hiện đại.
8.5. Khả năng tiên đoán và mô phỏng
Với khả năng mô tả và tính toán chi tiết, cường độ điện trường giúp các nhà vật lý và kỹ sư tiên đoán các hiện tượng điện từ và mô phỏng các hệ thống điện phức tạp, từ đó cải thiện các mô hình lý thuyết và ứng dụng trong thực tế.
Tóm lại, cường độ điện trường không chỉ là một đại lượng vật lý cơ bản mà còn là một công cụ mạnh mẽ trong việc nghiên cứu và ứng dụng các hiện tượng liên quan đến điện và từ trong đời sống và khoa học công nghệ.