Trong 1 Điện Trường Đều: Khái Niệm, Tính Toán Và Ứng Dụng

Điện trường đều là một khái niệm quan trọng trong vật lý, đặc biệt trong lĩnh vực điện học. Điện trường đều là loại điện trường có các đặc điểm đồng nhất, với vectơ cường độ điện trường tại mọi điểm đều có cùng phương, chiều và độ lớn. Điều này làm cho điện trường đều có nhiều ứng dụng quan trọng trong các lĩnh vực như điện tử, viễn thông và vật lý.

Đặc Điểm Của Điện Trường Đều

• Cường độ điện trường: Cường độ điện trường tại mọi điểm trong điện trường đều có giá trị như nhau. Vectơ cường độ điện trường luôn song song và cùng chiều với nhau.
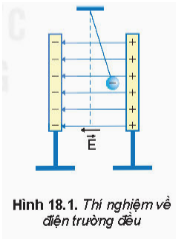
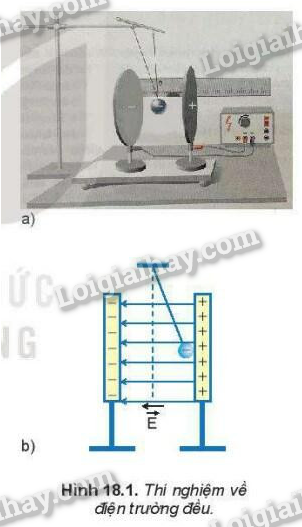
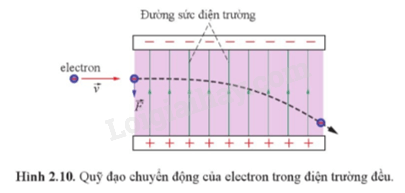
• Đường sức điện: Đường sức điện trong điện trường đều là các đường thẳng song song và cách đều nhau. Điều này giúp biểu diễn trực quan và dễ hiểu về sự phân bố của điện trường trong không gian.

Công Thức Liên Quan

Cường độ điện trường trong điện trường đều được xác định bằng công thức:

\[
E = \frac{U}{d}
\]

Trong đó:

• \(E\) là cường độ điện trường (V/m).
• \(U\) là hiệu điện thế giữa hai điểm (V).
• \(d\) là khoảng cách giữa hai điểm (m).

Ứng Dụng Của Điện Trường Đều

Điện trường đều có nhiều ứng dụng trong thực tiễn, bao gồm:

• Điện tử và viễn thông: Trong các hệ thống điện tử, điện trường đều giúp đảm bảo sự truyền tín hiệu ổn định và tránh hiện tượng nhiễu loạn.
• Thí nghiệm vật lý: Điện trường đều thường được sử dụng trong các thí nghiệm vật lý để nghiên cứu chuyển động của các hạt mang điện.
• Máy gia tốc hạt: Các máy gia tốc hạt sử dụng điện trường đều để điều khiển và tăng tốc các hạt mang điện trong quá trình thí nghiệm.

Bài Tập Về Điện Trường Đều

Dưới đây là một số bài tập minh họa về điện trường đều:

1. Bài tập 1: Tính cường độ điện trường trong một điện trường đều có hiệu điện thế 100V và khoảng cách giữa hai bản là 5cm.
2. Bài tập 2: Một hạt điện tích \(q = 2 \times 10^{-6} C\) chuyển động trong điện trường đều có cường độ điện trường \(E = 500 V/m\). Tính lực tác dụng lên hạt điện tích.

Kết Luận

Điện trường đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế. Việc hiểu rõ về điện trường đều và cách tính toán liên quan sẽ giúp ích rất nhiều trong các lĩnh vực như kỹ thuật điện, điện tử và vật lý học.

Điện trường đều là một loại điện trường đặc biệt, trong đó cường độ điện trường tại mọi điểm đều có cùng phương, chiều và độ lớn. Điều này có nghĩa là các đường sức điện trong điện trường đều luôn song song và cách đều nhau.

Cường độ điện trường trong điện trường đều được tính theo công thức:

\[
E = \frac{U}{d}
\]

Trong đó:

• \(E\) là cường độ điện trường (V/m).
• \(U\) là hiệu điện thế giữa hai điểm (V).
• \(d\) là khoảng cách giữa hai điểm (m).

Đặc tính đồng đều của điện trường đều giúp cho việc tính toán và phân tích lực tác dụng lên các hạt mang điện trở nên đơn giản hơn. Nó thường được sử dụng trong các thí nghiệm vật lý và ứng dụng thực tế liên quan đến điện từ.

Trong một điện trường đều, công thức tính toán liên quan đến lực điện và thế năng được xây dựng dựa trên mối quan hệ giữa cường độ điện trường \(E\), điện tích \(q\), và khoảng cách \(d\) giữa hai điểm trong điện trường.

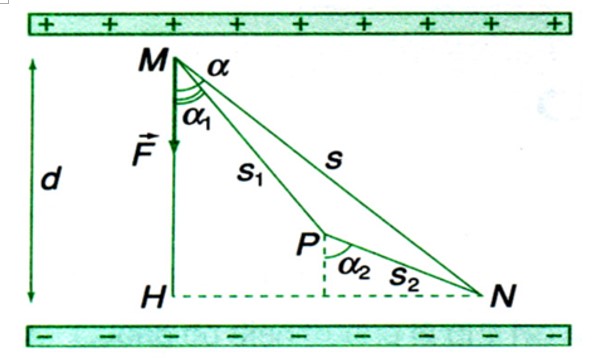
• Công của lực điện: Công \(A\) của lực điện tác dụng lên một điện tích \(q\) khi nó di chuyển từ điểm \(M\) đến \(N\) trong một điện trường đều được tính bằng công thức: \[ A = qEd \cos \theta \] Trong đó, \(E\) là cường độ điện trường, \(d\) là khoảng cách giữa hai điểm, và \(\theta\) là góc giữa vectơ cường độ điện trường và đường đi.
• Độ lớn của cường độ điện trường: Cường độ điện trường \(E\) giữa hai bản kim loại phẳng song song được tính bằng: \[ E = \frac{U}{d} \] Với \(U\) là hiệu điện thế giữa hai điểm, và \(d\) là khoảng cách giữa hai điểm trong điện trường.
• Thế năng điện: Thế năng \(W\) của điện tích \(q\) tại điểm \(A\) trong điện trường đều được xác định bởi công thức: \[ W = qEd \] Ở đây, \(d\) là khoảng cách từ điểm \(A\) đến điểm tham chiếu (thường chọn là điểm \(B\) có thế năng bằng 0).

Những công thức trên là cơ sở quan trọng để tính toán các đại lượng vật lý liên quan đến điện trường đều, giúp hiểu rõ hơn về các hiện tượng điện động lực học trong môi trường này.

Điện trường đều là một khái niệm quan trọng trong vật lý, được ứng dụng rộng rãi trong nhiều lĩnh vực kỹ thuật và công nghệ. Dưới đây là một số ứng dụng tiêu biểu của điện trường đều:

• Máy biến thế: Trong các máy biến thế, điện trường đều được sử dụng để truyền tải điện năng một cách hiệu quả. Các dây dẫn được sắp xếp sao cho cường độ điện trường luôn đồng đều, giúp giảm thiểu tổn hao năng lượng.
• Máy gia tốc hạt: Trong các máy gia tốc hạt, điện trường đều được sử dụng để tăng tốc các hạt tích điện, nhờ vào lực điện tác dụng theo một hướng không đổi, giúp các hạt đạt được vận tốc cao trong khoảng cách ngắn.
• Màng lọc tĩnh điện: Các màng lọc sử dụng điện trường đều để loại bỏ các hạt bụi và tạp chất trong không khí. Hạt bụi bị tích điện và bị hút vào các bản cực, giúp làm sạch không khí hiệu quả.
• Thiết bị hiển thị LCD: Màn hình LCD sử dụng điện trường đều để điều khiển sự sắp xếp của các tinh thể lỏng, tạo ra hình ảnh rõ nét và chính xác.
• Cảm biến điện trường: Điện trường đều được ứng dụng trong các cảm biến để đo lường sự thay đổi của điện áp, phát hiện các đối tượng trong khoảng cách gần và nhiều ứng dụng khác trong công nghệ cảm biến.

Các ứng dụng trên không chỉ minh chứng cho vai trò quan trọng của điện trường đều trong kỹ thuật mà còn mở ra nhiều hướng phát triển mới trong công nghệ hiện đại.

Dưới đây là một số bài tập tiêu biểu liên quan đến điện trường đều nhằm giúp học sinh củng cố kiến thức và nắm vững các khái niệm cơ bản.

1. Bài tập 1: Một điện tích điểm \(q = 5 \times 10^{-6} C\) được đặt trong một điện trường đều có cường độ \(E = 2 \times 10^5 \, V/m\). Tính công của lực điện khi điện tích di chuyển một đoạn đường thẳng dài \(d = 0.2 \, m\) theo phương của điện trường.

   Lời giải:

   • Công thức tính công của lực điện: \[ A = qEd \]
   • Thay số: \[ A = (5 \times 10^{-6}) \times (2 \times 10^5) \times 0.2 = 0.2 \, J \]
2. Bài tập 2: Giữa hai bản kim loại phẳng song song cách nhau \(d = 1 \, cm\) có một điện trường đều với cường độ \(E = 10^4 \, V/m\). Tính hiệu điện thế giữa hai bản.

   Lời giải:

   • Công thức tính hiệu điện thế: \[ U = Ed \]
   • Thay số: \[ U = 10^4 \times 0.01 = 100 \, V \]
3. Bài tập 3: Một hạt mang điện tích \(q = 1.6 \times 10^{-19} \, C\) di chuyển từ điểm \(A\) đến \(B\) trong một điện trường đều với cường độ \(E = 5 \times 10^4 \, V/m\). Biết khoảng cách giữa \(A\) và \(B\) là \(d = 0.05 \, m\). Tính công của lực điện và thế năng tại hai điểm \(A\) và \(B\).

   Lời giải:

   • Công của lực điện: \[ A = qEd = 1.6 \times 10^{-19} \times 5 \times 10^4 \times 0.05 = 4 \times 10^{-18} \, J \]
   • Thế năng tại \(A\): \[ W_A = qEd_A = 1.6 \times 10^{-19} \times 5 \times 10^4 \times 0 = 0 \, J \]
   • Thế năng tại \(B\): \[ W_B = qEd_B = 1.6 \times 10^{-19} \times 5 \times 10^4 \times 0.05 = 4 \times 10^{-18} \, J \]

Những bài tập trên giúp học sinh rèn luyện kỹ năng tính toán và áp dụng các công thức liên quan đến điện trường đều, từ đó hiểu rõ hơn về các hiện tượng vật lý trong môi trường này.