Đặt Một Điện Tích q Trong Điện Trường Đều E: Khái Niệm, Công Thức và Ứng Dụng Thực Tế

Khi đặt một điện tích \( q \) trong một điện trường đều \( \vec{E} \), lực điện \( \vec{F} \) tác dụng lên điện tích sẽ được xác định bởi công thức:

\[
\vec{F} = q \times \vec{E}
\]

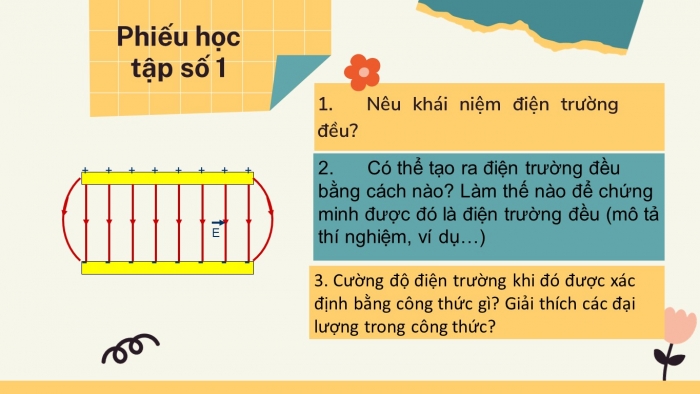
1. Khái niệm điện trường đều

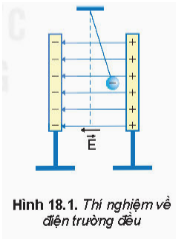
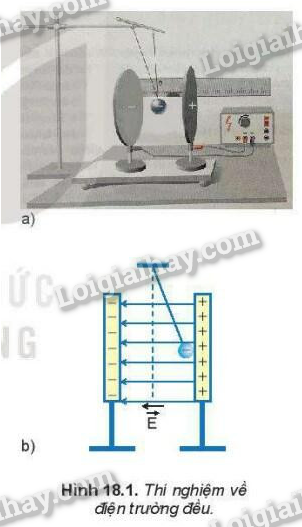
Điện trường đều là điện trường có các đường sức song song, cùng chiều và cách đều nhau. Cường độ điện trường \( \vec{E} \) tại mọi điểm trong điện trường đều có cùng độ lớn và hướng. Trong thực tế, điện trường đều thường được tạo ra giữa hai bản kim loại song song và được tích điện trái dấu.

2. Lực điện tác dụng lên điện tích

Khi một điện tích \( q \) được đặt trong điện trường đều \( \vec{E} \), lực điện tác dụng lên điện tích được tính theo công thức:

\[
\vec{F} = q \times \vec{E}
\]

Trong đó:

• \( \vec{F} \) là lực điện (N).
• \( q \) là điện tích (C).
• \( \vec{E} \) là cường độ điện trường (V/m).

Hướng của lực điện \( \vec{F} \) sẽ phụ thuộc vào dấu của điện tích \( q \). Nếu \( q \) là điện tích dương, \( \vec{F} \) cùng hướng với \( \vec{E} \). Nếu \( q \) là điện tích âm, \( \vec{F} \) ngược hướng với \( \vec{E} \).

3. Công của lực điện

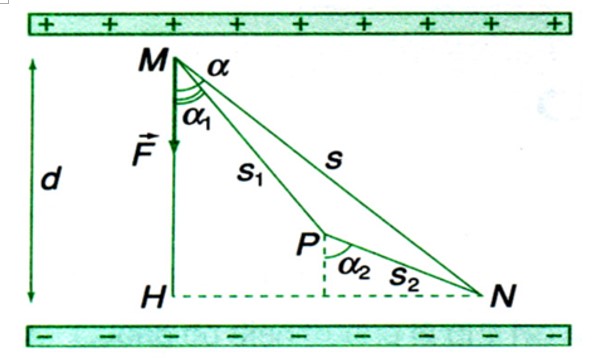
Khi một điện tích \( q \) di chuyển từ điểm M đến điểm N trong điện trường đều \( \vec{E} \), công của lực điện \( A \) được xác định bởi công thức:

\[
A = q \times E \times d \times \cos\theta
\]

Trong đó:

• \( A \) là công của lực điện (J).
• \( d \) là khoảng cách giữa M và N (m).
• \( \theta \) là góc giữa vectơ \( \vec{E} \) và vectơ dịch chuyển.

4. Ứng dụng trong thực tế

Điện trường đều được sử dụng trong nhiều ứng dụng thực tế, bao gồm:

• Thí nghiệm điện trường: Dùng trong các thí nghiệm nghiên cứu về lực điện và điện trường.
• Máy gia tốc hạt: Điện trường đều được sử dụng để tăng tốc các hạt tích điện.
• Tụ điện phẳng: Trong tụ điện, điện trường giữa hai bản kim loại được coi là đều.

5. Bài tập ví dụ

Ví dụ: Một điện tích \( q = 2 \times 10^{-6} \, \text{C} \) được đặt trong điện trường đều có cường độ \( E = 1000 \, \text{V/m} \). Tính lực điện tác dụng lên điện tích.

Lời giải:

Áp dụng công thức \( \vec{F} = q \times \vec{E} \):

\[
\vec{F} = 2 \times 10^{-6} \times 1000 = 2 \times 10^{-3} \, \text{N}
\]

Vậy lực điện tác dụng lên điện tích là \( 2 \times 10^{-3} \, \text{N} \).

Điện trường là một khái niệm quan trọng trong vật lý, biểu thị vùng không gian xung quanh một điện tích mà tại đó, các điện tích khác chịu tác dụng của lực điện. Điện trường được tạo ra bởi các điện tích và thể hiện sự tác động của điện tích này lên điện tích khác thông qua lực Coulomb.

Cường độ điện trường, ký hiệu là \( \mathbf{E} \), là đại lượng vector đặc trưng cho độ lớn và hướng của điện trường tại mỗi điểm trong không gian. Nó được xác định bằng công thức:

\[
\mathbf{E} = \frac{\mathbf{F}}{q}
\]

Trong đó:

• \( \mathbf{E} \) là cường độ điện trường (đơn vị: V/m).
• \( \mathbf{F} \) là lực điện tác dụng lên điện tích thử \( q \) (đơn vị: N).
• \( q \) là điện tích thử (đơn vị: C).

Nếu đặt một điện tích thử \( q \) trong một điện trường đều \( \mathbf{E} \), thì lực điện tác dụng lên điện tích đó được tính bằng:

\[
\mathbf{F} = q \mathbf{E}
\]

Điện trường đều là loại điện trường có vector cường độ điện trường \( \mathbf{E} \) tại mọi điểm đều có cùng phương, chiều và độ lớn. Một ví dụ tiêu biểu của điện trường đều là điện trường giữa hai bản kim loại phẳng song song, tích điện trái dấu và cách nhau một khoảng không đáng kể.

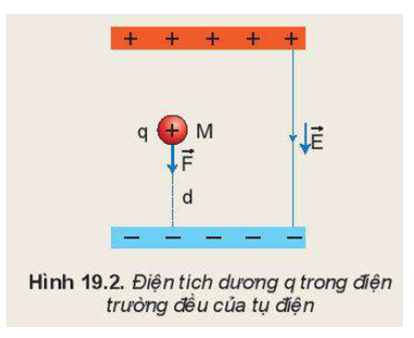
Khi đặt một điện tích \( q \) trong một điện trường đều \( \mathbf{E} \), điện tích này sẽ chịu tác dụng của một lực điện. Lực này có phương và chiều trùng với vector cường độ điện trường và được xác định theo công thức:

\[
\mathbf{F} = q \mathbf{E}
\]

Trong đó:

• \( \mathbf{F} \) là lực điện tác dụng lên điện tích \( q \) (đơn vị: Newton, N).
• \( q \) là điện tích (đơn vị: Coulomb, C).
• \( \mathbf{E} \) là cường độ điện trường (đơn vị: V/m).

Lực điện \( \mathbf{F} \) này có một số đặc điểm quan trọng:

1. Phương và chiều của lực: Lực điện có phương và chiều trùng với phương và chiều của vector cường độ điện trường \( \mathbf{E} \). Nếu \( q > 0 \), lực \( \mathbf{F} \) cùng chiều với \( \mathbf{E} \). Nếu \( q < 0 \), lực \( \mathbf{F} \) ngược chiều với \( \mathbf{E} \).
2. Độ lớn của lực: Độ lớn của lực \( \mathbf{F} \) tỉ lệ thuận với độ lớn của điện tích \( q \) và cường độ điện trường \( \mathbf{E} \).
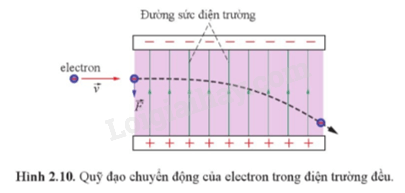
3. Tác động đến chuyển động: Lực điện tác dụng lên \( q \) sẽ làm cho điện tích di chuyển. Nếu ban đầu điện tích đứng yên, lực này sẽ làm nó chuyển động theo phương của \( \mathbf{E} \). Nếu điện tích đang chuyển động, lực điện sẽ thay đổi quỹ đạo của nó.

Như vậy, lực điện không chỉ quyết định phương và chiều di chuyển của điện tích mà còn ảnh hưởng trực tiếp đến vận tốc và quỹ đạo chuyển động của điện tích trong điện trường đều.

Trong điện trường đều, các công thức tính toán liên quan đến cường độ điện trường, lực điện, và công của lực điện thường xuyên được sử dụng để giải các bài toán vật lý. Dưới đây là các công thức cơ bản và cách sử dụng chúng:

1. Công thức tính cường độ điện trường \( \mathbf{E} \):

Cường độ điện trường tại một điểm trong không gian được xác định bằng tỉ số giữa lực điện \( \mathbf{F} \) tác dụng lên một điện tích thử \( q \) và độ lớn của điện tích đó:

\[
\mathbf{E} = \frac{\mathbf{F}}{q}
\]

• \( \mathbf{E} \) là cường độ điện trường (V/m).
• \( \mathbf{F} \) là lực điện tác dụng lên điện tích (N).
• \( q \) là điện tích thử (C).
2. Công thức tính lực điện tác dụng lên điện tích \( q \):

Khi điện tích \( q \) được đặt trong điện trường \( \mathbf{E} \), lực điện tác dụng lên nó được tính bằng:

\[
\mathbf{F} = q \mathbf{E}
\]

Độ lớn của lực này sẽ quyết định sự di chuyển của điện tích trong điện trường đều.

3. Công thức tính công của lực điện khi điện tích di chuyển:

Công của lực điện khi một điện tích \( q \) di chuyển trong điện trường đều được xác định bằng:

\[
A = q \mathbf{E} \cdot d \cdot \cos \theta
\]

• \( A \) là công của lực điện (J).
• \( d \) là quãng đường điện tích di chuyển (m).
• \( \theta \) là góc giữa vector cường độ điện trường và phương chuyển động của điện tích.

Khi \( \theta = 0^\circ \) (điện tích di chuyển theo hướng của \( \mathbf{E} \)), công của lực điện đạt giá trị lớn nhất.

Những công thức trên là cơ bản và thường xuyên được áp dụng để giải các bài toán về điện trường đều, từ việc tính toán lực điện, cường độ điện trường, đến việc xác định công của lực điện khi điện tích di chuyển trong điện trường.

Điện trường đều không chỉ là một khái niệm lý thuyết trong vật lý, mà còn có nhiều ứng dụng thực tế trong đời sống và công nghệ. Dưới đây là một số ứng dụng quan trọng của điện trường đều:

1. Ứng dụng trong các thiết bị điện tử:

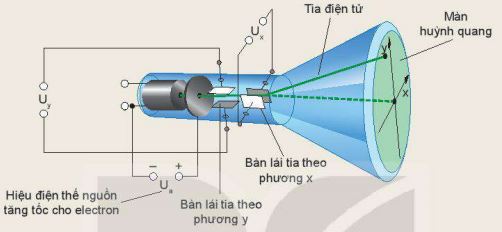
Điện trường đều được ứng dụng rộng rãi trong các thiết bị điện tử như tụ điện. Trong tụ điện, điện trường đều được tạo ra giữa hai bản cực và đóng vai trò quan trọng trong việc lưu trữ năng lượng. Điện trường cũng được sử dụng trong ống phóng điện tử (CRT), mà trước đây được dùng trong màn hình TV và máy tính, để điều khiển đường đi của các electron.

2. Ứng dụng trong công nghệ và đời sống:

Điện trường đều có mặt trong nhiều công nghệ hiện đại. Ví dụ, trong công nghệ in phun mực, điện trường đều giúp điều khiển các giọt mực bắn ra từ đầu phun để tạo ra hình ảnh trên giấy. Hơn nữa, điện trường đều còn được sử dụng trong các bộ lọc tĩnh điện, giúp loại bỏ bụi và các hạt ô nhiễm từ không khí, mang lại lợi ích lớn trong việc bảo vệ môi trường và sức khỏe con người.

3. Ứng dụng trong y tế:

Trong y học, điện trường đều được ứng dụng trong một số thiết bị như máy chụp X-quang, nơi điện trường đều được dùng để gia tốc các electron, tạo ra tia X dùng trong hình ảnh y khoa. Điện trường còn có vai trò trong các thiết bị y tế hiện đại như máy MRI, giúp chẩn đoán và theo dõi bệnh lý một cách hiệu quả.

Như vậy, điện trường đều không chỉ là một khái niệm cơ bản trong vật lý mà còn là nền tảng cho nhiều ứng dụng quan trọng trong công nghệ, y tế và đời sống hàng ngày.

Để nắm vững kiến thức về điện trường đều và lực điện tác dụng lên điện tích \( q \), việc luyện tập với các bài tập là rất quan trọng. Dưới đây là các dạng bài tập phổ biến và phương pháp giải tương ứng:

1. Bài tập xác định cường độ điện trường \( \mathbf{E} \):

Dạng bài tập này yêu cầu tính cường độ điện trường tại một điểm khi biết lực điện \( \mathbf{F} \) tác dụng lên một điện tích thử \( q \). Phương pháp giải:

• Sử dụng công thức \( \mathbf{E} = \frac{\mathbf{F}}{q} \).
• Xác định phương, chiều của \( \mathbf{E} \) dựa trên dấu của điện tích \( q \).
2. Bài tập tính lực điện \( \mathbf{F} \) tác dụng lên điện tích \( q \):

Bài tập yêu cầu xác định lực điện khi biết cường độ điện trường và điện tích. Phương pháp giải:

• Sử dụng công thức \( \mathbf{F} = q \mathbf{E} \).
• Lưu ý phương và chiều của lực điện dựa trên dấu của \( q \) (nếu \( q > 0 \), lực cùng chiều với \( \mathbf{E} \); nếu \( q < 0 \), lực ngược chiều).
3. Bài tập tính công của lực điện:

Dạng bài tập này thường liên quan đến việc tính công lực điện khi điện tích di chuyển trong điện trường đều. Phương pháp giải:

• Sử dụng công thức \( A = q \mathbf{E} \cdot d \cdot \cos \theta \).
• Xác định \( d \) là quãng đường điện tích di chuyển, \( \theta \) là góc giữa vector cường độ điện trường và phương chuyển động.
4. Bài tập nâng cao:

Dạng này thường kết hợp nhiều kiến thức và yêu cầu tính toán phức tạp hơn, ví dụ như tính toán khi điện tích di chuyển theo đường cong, hoặc khi điện trường không đều.

• Phân tích kỹ đề bài để xác định các đại lượng cần thiết.
• Sử dụng phương pháp chia nhỏ bài toán thành các bước để giải quyết từng phần.
• Áp dụng tích phân trong trường hợp cần thiết, khi quỹ đạo của điện tích không phải là đường thẳng.

Việc luyện tập với các dạng bài tập trên sẽ giúp học sinh nắm vững các khái niệm và kỹ năng tính toán liên quan đến điện trường đều, từ đó giải quyết tốt các bài toán trong học tập và thi cử.