Chủ đề các dạng bài tập về điện trường đều: Các dạng bài tập về điện trường đều là chủ đề quan trọng trong chương trình Vật lý 11. Bài viết này tổng hợp các dạng bài tập phổ biến, phương pháp giải cụ thể và những mẹo hữu ích giúp bạn nắm vững kiến thức và tự tin vượt qua các kỳ thi. Đừng bỏ lỡ những kỹ thuật giải toán quan trọng để đạt điểm cao!
Mục lục
- Các Dạng Bài Tập Về Điện Trường Đều
- 1. Khái Niệm Và Đặc Điểm Của Điện Trường Đều
- 2. Phương Pháp Xác Định Cường Độ Điện Trường
- 3. Bài Tập Về Sự Cân Bằng Của Điện Tích
- 4. Vẽ Đường Sức Điện Trong Điện Trường Đều
- 5. Chuyển Động Của Điện Tích Trong Điện Trường
- 6. Các Bài Tập Vận Dụng Cao
- 7. Tài Liệu Tham Khảo Và Bài Tập Tự Luyện
Các Dạng Bài Tập Về Điện Trường Đều
Điện trường đều là một trong những khái niệm quan trọng trong Vật lý 11. Dưới đây là tổng hợp các dạng bài tập thường gặp và phương pháp giải.
1. Xác Định Cường Độ Điện Trường
- Dạng bài: Tính toán cường độ điện trường tại một điểm do nhiều điện tích gây ra.
- Phương pháp: Sử dụng quy tắc cộng véctơ theo quy tắc hình bình hành hoặc hình chiếu lên các trục tọa độ: \[ E_{tổng} = \sqrt{E_1^2 + E_2^2 + 2E_1E_2\cos\alpha} \]
2. Sự Cân Bằng Của Điện Tích Trong Điện Trường
- Dạng bài: Khảo sát sự cân bằng của một điện tích trong điện trường đều.
- Phương pháp: Tổng hợp các lực tác dụng lên điện tích và đặt điều kiện cân bằng: \[ \sum F = 0 \implies E_{x} = E_{y} = 0 \]
3. Xác Định Đường Sức Điện Trong Điện Trường Đều
- Dạng bài: Vẽ và phân tích hướng của các đường sức điện trong điện trường đều.
- Phương pháp: Các đường sức luôn là những đường thẳng song song và có cùng chiều với hướng của lực điện tác dụng lên điện tích dương thử.
4. Chuyển Động Của Điện Tích Trong Điện Trường Đều
- Dạng bài: Tính vận tốc và quỹ đạo của điện tích khi nó chuyển động trong điện trường đều.
- Phương pháp: Áp dụng định luật Newton và các công thức động học: \[ a = \frac{qE}{m}, \quad v = v_0 + at, \quad x = x_0 + v_0t + \frac{1}{2}at^2 \]
5. Bài Tập Vận Dụng Cao
Các bài tập nâng cao kết hợp nhiều khái niệm như định luật Coulomb, định lý Gauss, và các phương pháp tính toán phức tạp khác để giải các bài toán điện trường đều.
Tài Liệu Liên Quan

.png)
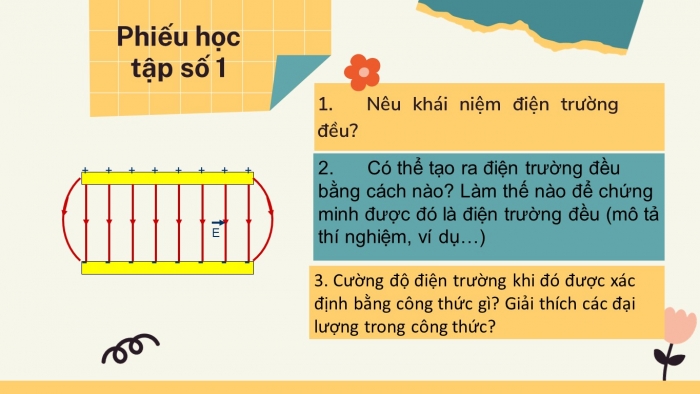
1. Khái Niệm Và Đặc Điểm Của Điện Trường Đều
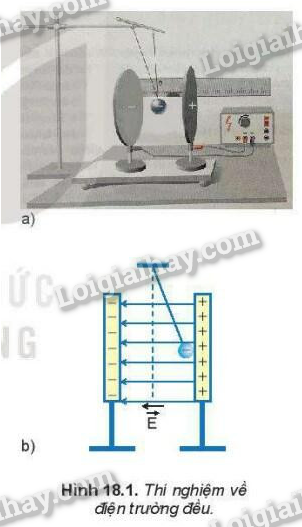
Điện trường đều là một loại điện trường mà tại mọi điểm trong không gian, cường độ điện trường có độ lớn và hướng không đổi. Trong thực tế, điện trường đều thường được tạo ra giữa hai bản kim loại phẳng song song và cách đều nhau.
Cường độ điện trường đều được ký hiệu là \(\vec{E}\) và được tính bằng công thức:
trong đó:
- \(U\): Hiệu điện thế giữa hai bản (V)
- \(d\): Khoảng cách giữa hai bản (m)
Đặc điểm của điện trường đều:
- Các đường sức điện là những đường thẳng song song và cách đều nhau.
- Cường độ điện trường \(\vec{E}\) có độ lớn và hướng không đổi trong toàn bộ không gian giữa hai bản điện tích.
- Điện trường đều được ứng dụng trong các thiết bị như tụ điện phẳng, thiết bị phân tích quỹ đạo hạt điện tích, v.v.
2. Phương Pháp Xác Định Cường Độ Điện Trường
Cường độ điện trường \(\vec{E}\) là đại lượng đặc trưng cho độ mạnh yếu của điện trường tại một điểm và được xác định thông qua lực tác dụng lên điện tích thử trong điện trường. Dưới đây là các phương pháp cơ bản để xác định cường độ điện trường:
- Phương pháp dùng định nghĩa:
Theo định nghĩa, cường độ điện trường tại một điểm được tính bằng công thức:
\[ \vec{E} = \frac{\vec{F}}{q} \]trong đó:
- \(\vec{F}\): Lực điện tác dụng lên điện tích thử (N)
- \(q\): Điện tích thử (C)
- Phương pháp tính cường độ điện trường của điện tích điểm:
Cường độ điện trường tại một điểm cách điện tích điểm một khoảng \(r\) được tính bằng công thức:
\[ E = k \cdot \frac{|q|}{r^2} \]trong đó:
- \(k\): Hằng số điện môi (\(k \approx 9 \times 10^9 \, \text{N·m}^2/\text{C}^2\))
- \(q\): Điện tích điểm (C)
- \(r\): Khoảng cách từ điện tích đến điểm đang xét (m)
- Phương pháp tính cường độ điện trường đều:
Trong điện trường đều, cường độ điện trường được xác định bởi:
\[ E = \frac{U}{d} \]trong đó:
- \(U\): Hiệu điện thế giữa hai bản (V)
- \(d\): Khoảng cách giữa hai bản (m)
- Phương pháp cộng vectơ:
Khi có nhiều điện tích gây ra điện trường tại một điểm, cường độ điện trường tổng hợp được xác định bằng tổng vectơ của các cường độ điện trường do từng điện tích gây ra:
\[ \vec{E}_{\text{tổng}} = \vec{E}_1 + \vec{E}_2 + \dots + \vec{E}_n \]
Việc áp dụng đúng các phương pháp trên sẽ giúp bạn xác định chính xác cường độ điện trường trong nhiều tình huống bài tập khác nhau.

3. Bài Tập Về Sự Cân Bằng Của Điện Tích
Bài tập về sự cân bằng của điện tích thường xoay quanh các tình huống mà các lực điện cân bằng nhau, khiến cho điện tích đứng yên hoặc duy trì vị trí. Dưới đây là các dạng bài tập phổ biến:
- Dạng bài tập về hai điện tích đặt trong điện trường:
Xác định vị trí cân bằng của một điện tích đặt trong điện trường đều khi chịu tác dụng của cả lực điện trường và lực từ một điện tích khác. Bài toán này thường yêu cầu:
- Xác định phương trình cân bằng: \(\vec{F}_{\text{điện trường}} + \vec{F}_{\text{tĩnh điện}} = 0\)
- Tính toán cường độ điện trường \(\vec{E}\) và lực tương tác \(\vec{F}\)
- Dạng bài tập về điện tích treo trên dây:
Trong bài tập này, điện tích được treo bằng một sợi dây trong điện trường đều. Để cân bằng, các lực tác dụng bao gồm:
- Lực điện: \(\vec{F}_{\text{điện}} = q\vec{E}\)
- Lực căng dây: \(\vec{T}\)
- Trọng lực: \(\vec{P} = mg\)
Bài toán yêu cầu tính góc lệch của dây so với phương thẳng đứng hoặc độ lớn các lực liên quan.
- Dạng bài tập về cân bằng của nhiều điện tích đồng thời:
Bài toán này liên quan đến nhiều điện tích tương tác lẫn nhau trong một không gian, yêu cầu xác định vị trí cân bằng của từng điện tích. Bài toán thường áp dụng:
- Nguyên lý chồng chất lực: \(\vec{F}_{\text{tổng}} = \vec{F}_1 + \vec{F}_2 + \dots + \vec{F}_n\)
- Định luật Coulomb: \(\vec{F} = k \cdot \frac{|q_1 \cdot q_2|}{r^2}\)
Việc giải quyết bài tập liên quan đến sự cân bằng của điện tích yêu cầu hiểu rõ về lý thuyết điện trường và phương pháp xác định lực, từ đó áp dụng vào từng dạng bài một cách chính xác và hiệu quả.

XEM THÊM:
4. Vẽ Đường Sức Điện Trong Điện Trường Đều
Vẽ đường sức điện trong điện trường đều giúp minh họa rõ ràng hướng và tính chất của lực tác dụng lên các điện tích trong điện trường. Đặc điểm chính của điện trường đều là các đường sức có dạng song song, thẳng, và cách đều nhau. Dưới đây là quy trình vẽ chi tiết:
- Bước 1: Xác định chiều của điện trường
Điện trường đều thường sinh ra bởi hai bản cực song song, một bản mang điện tích dương và một bản mang điện tích âm. Chiều của điện trường luôn đi từ bản dương sang bản âm.
- Bước 2: Vẽ các đường sức song song
Trong điện trường đều, các đường sức là những đường thẳng song song và cách đều nhau. Mỗi đường sức thể hiện hướng của lực điện tác dụng lên điện tích dương.
- Bước 3: Biểu diễn tính chất đều của điện trường
Các đường sức trong điện trường đều không bị cong, không hội tụ hay phân kỳ, cho thấy tính chất đồng đều và nhất quán của lực điện trường trong không gian.
Khi vẽ, cần chú ý rằng mật độ đường sức không thay đổi, đảm bảo sự nhất quán trong độ lớn của cường độ điện trường. Kết quả là một hình ảnh trực quan về cách lực điện tác động trong môi trường điện trường đều.

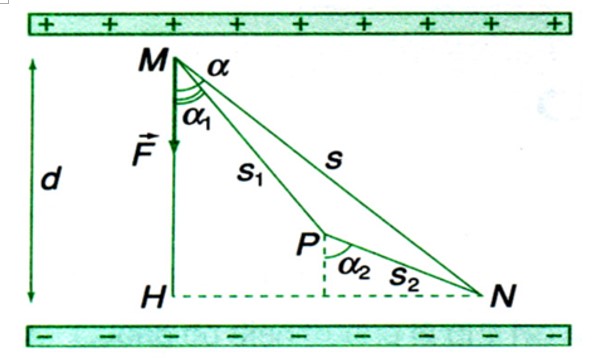
5. Chuyển Động Của Điện Tích Trong Điện Trường
Chuyển động của điện tích trong điện trường đều có thể được hiểu qua sự tác động của lực điện lên điện tích đó. Dưới đây là các bước mô tả chi tiết quá trình chuyển động:
- Bước 1: Xác định lực điện tác dụng lên điện tích
Trong điện trường đều, lực điện \( \vec{F} \) tác dụng lên điện tích \( q \) được tính theo công thức: \( \vec{F} = q \cdot \vec{E} \), trong đó \( \vec{E} \) là cường độ điện trường.
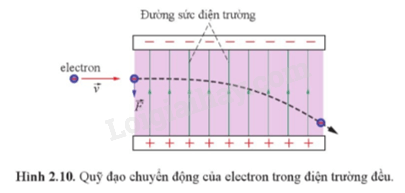
- Bước 2: Phân tích chuyển động của điện tích
Khi điện tích \( q > 0 \), lực \( \vec{F} \) cùng hướng với điện trường \( \vec{E} \). Ngược lại, khi \( q < 0 \), lực \( \vec{F} \) ngược hướng với \( \vec{E} \). Điều này dẫn đến sự di chuyển của điện tích theo hướng của lực tác dụng.
- Bước 3: Phương trình mô tả chuyển động
Quá trình chuyển động của điện tích trong điện trường đều có thể được mô tả bằng phương trình chuyển động thẳng đều hoặc thẳng biến đổi đều tùy thuộc vào điều kiện cụ thể của bài toán. Gia tốc \( a \) của điện tích được tính bằng: \( a = \frac{F}{m} = \frac{q \cdot E}{m} \), trong đó \( m \) là khối lượng của điện tích.
Kết luận, điện tích trong điện trường đều sẽ chịu tác động của một lực không đổi, dẫn đến chuyển động có quỹ đạo thẳng theo chiều của lực điện.
6. Các Bài Tập Vận Dụng Cao
Dưới đây là một số bài tập vận dụng cao về điện trường đều, tập trung vào các tình huống phức tạp và yêu cầu sử dụng nhiều kiến thức tổng hợp để giải quyết:
6.1. Bài Tập Kết Hợp Định Luật Coulomb
Ví dụ, xét một hệ gồm hai điện tích \( q_1 \) và \( q_2 \) đặt trong điện trường đều \( \mathbf{E} \). Cần tìm vị trí của một điểm trong không gian sao cho lực tổng hợp tác dụng lên điện tích tại điểm đó bằng không. Bài toán yêu cầu:
- Tính lực điện từ giữa hai điện tích \( F_{12} = k_e \frac{|q_1 \cdot q_2|}{r^2} \), trong đó \( r \) là khoảng cách giữa hai điện tích.
- Xác định cường độ điện trường tổng hợp \( \mathbf{E}_{\text{tổng hợp}} \) tại điểm cần tìm.
- Thiết lập phương trình cân bằng lực \( \mathbf{F}_{\text{tổng hợp}} = 0 \), từ đó giải ra vị trí cần tìm.
6.2. Bài Tập Sử Dụng Định Lý Gauss
Bài toán phức tạp hơn có thể liên quan đến việc sử dụng định lý Gauss để tính cường độ điện trường trong các hệ hình học phức tạp. Ví dụ:
- Xét một hình trụ dài, điện tích phân bố đều theo trục của nó. Sử dụng định lý Gauss để tính cường độ điện trường bên trong và bên ngoài hình trụ.
- Sử dụng bề mặt Gauss là một hình trụ đồng trục với hình trụ đã cho, thiết lập các phương trình từ định lý Gauss \( \oint \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{bên trong}}}{\epsilon_0} \).
- Giải hệ phương trình để tìm biểu thức của cường độ điện trường \( \mathbf{E}(r) \) theo khoảng cách \( r \) từ trục của hình trụ.
Các bài tập trên không chỉ giúp học sinh hiểu sâu hơn về lý thuyết điện trường đều mà còn rèn luyện kỹ năng giải quyết các vấn đề phức tạp, yêu cầu tư duy tổng hợp và khả năng áp dụng nhiều kiến thức liên môn.

7. Tài Liệu Tham Khảo Và Bài Tập Tự Luyện
Dưới đây là danh sách các tài liệu tham khảo và bài tập tự luyện nhằm củng cố kiến thức về điện trường đều. Các bài tập được phân loại theo độ khó và kèm theo hướng dẫn chi tiết, giúp học sinh dễ dàng ôn tập và nâng cao kỹ năng giải bài tập.
7.1. Tài Liệu Tham Khảo
- - Tài liệu cung cấp nhiều dạng bài tập khác nhau từ cơ bản đến nâng cao, giúp học sinh luyện tập và nắm vững kiến thức.
- - Bộ tài liệu trắc nghiệm với lời giải chi tiết, giúp học sinh tự đánh giá khả năng và cải thiện kỹ năng làm bài.
- - Tài liệu tập trung vào các dạng bài tập liên quan đến lực điện trường, phù hợp cho học sinh chuẩn bị cho các kỳ thi quan trọng.
7.2. Bài Tập Tự Luyện
Dưới đây là một số bài tập tự luyện nhằm giúp bạn đọc củng cố kiến thức về điện trường đều:
- Hai điện tích điểm \( q_1 \) và \( q_2 \) đặt cách nhau một khoảng r trong chân không. Xác định lực điện tổng hợp tác dụng lên một điện tích thử \( q_0 \) đặt tại điểm M, cách \( q_1 \) và \( q_2 \) lần lượt các khoảng \( r_1 \) và \( r_2 \).
- Một điện tích \( q = 5 \, \mu C \) di chuyển dọc theo đường sức điện trong một điện trường đều có cường độ điện trường \( E = 200 \, V/m \). Tính công của lực điện khi điện tích di chuyển từ điểm A đến điểm B cách nhau 10 cm.
- Một hệ gồm ba điện tích điểm \( q_1 \), \( q_2 \), và \( q_3 \) đặt tại ba đỉnh của một tam giác đều. Tính cường độ điện trường tổng hợp tại điểm còn lại của tam giác.
- Cho hai điện tích \( q_1 = 3 \times 10^{-6} \, C \) và \( q_2 = -2 \times 10^{-6} \, C \) đặt tại các điểm A và B cách nhau 5 cm. Tính điện thế tại điểm C nằm trên đường trung trực của đoạn AB và cách AB một khoảng 4 cm.
- Một tụ điện phẳng có điện dung \( C = 20 \, \mu F \) được nạp điện đến hiệu điện thế \( U = 120 \, V \). Xác định cường độ điện trường giữa hai bản tụ và điện tích lưu trữ trên các bản tụ.
Các bài tập trên nhằm giúp học sinh nắm vững lý thuyết và ứng dụng vào thực tế, chuẩn bị tốt nhất cho các kỳ thi quan trọng như thi tốt nghiệp và thi đại học.