Vectơ Cường Độ Điện Trường Tại Mỗi Điểm Có Chiều: Khái Niệm, Tính Toán Và Ứng Dụng Thực Tế

Véctơ cường độ điện trường là một khái niệm quan trọng trong vật lý điện, đặc biệt là trong các bài học về điện trường và lực điện. Véctơ này mô tả cường độ và hướng của lực điện tại một điểm trong không gian do các điện tích gây ra.

Công Thức Cơ Bản

Công thức tính véctơ cường độ điện trường \( \vec{E} \) tại một điểm trong điện trường được biểu diễn như sau:

\[
\vec{E} = \frac{\vec{F}}{q}
\]

Trong đó:

• \( \vec{E} \): Véctơ cường độ điện trường.
• \( \vec{F} \): Lực điện tác dụng lên điện tích thử.
• \( q \): Điện tích thử (đơn vị Coulomb).

Công Thức Cường Độ Điện Trường Tại Điện Tích Điểm

Với một điện tích điểm \( Q \), cường độ điện trường tại một điểm cách điện tích một khoảng cách \( r \) được tính theo công thức:

\[
\vec{E} = k \cdot \frac{Q}{r^2} \cdot \hat{r}
\]

Trong đó:

• \( k \): Hằng số Coulomb \( (k \approx 8.99 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2) \).
• \( Q \): Điện tích gây ra điện trường.
• \( r \): Khoảng cách từ điện tích đến điểm xét.
• \( \hat{r} \): Véctơ đơn vị chỉ hướng từ điện tích đến điểm xét.

Đặc Điểm Của Véctơ Cường Độ Điện Trường

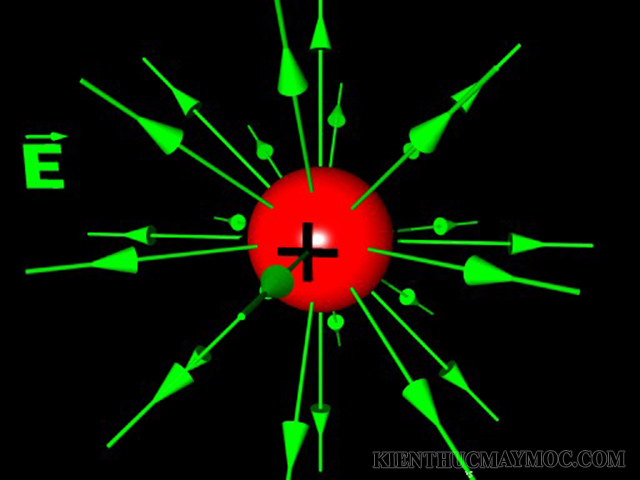
• Véctơ cường độ điện trường tại mỗi điểm có phương và chiều xác định, phụ thuộc vào dấu của điện tích \( Q \).
• Với điện tích dương, véctơ cường độ điện trường có hướng ra xa điện tích. Ngược lại, với điện tích âm, véctơ có hướng về phía điện tích.
• Cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách \( r \) từ điện tích đến điểm xét.

Ứng Dụng Trong Thực Tế

Cường độ điện trường là một khái niệm thiết yếu trong nhiều lĩnh vực khoa học và kỹ thuật. Dưới đây là một số ứng dụng tiêu biểu:

• Thiết kế các thiết bị điện tử: Hiểu về cường độ điện trường giúp các kỹ sư thiết kế các linh kiện và mạch điện tử một cách hiệu quả.
• Công nghệ y tế: Điện trường được ứng dụng trong các thiết bị y tế như máy điện tâm đồ và các thiết bị trị liệu.
• Công nghệ môi trường: Điện trường được sử dụng trong quá trình xử lý khí thải công nghiệp và xử lý ô nhiễm môi trường.
• Khám phá vũ trụ: Nghiên cứu các hiện tượng vật lý trong không gian như bão từ và dòng điện trong plasma.

Điện Trường Đều

Điện trường đều là một loại điện trường đặc biệt trong đó véctơ cường độ điện trường có cùng phương, chiều và độ lớn tại mọi điểm. Đường sức điện của điện trường đều là những đường thẳng song song cách đều nhau.

\[
E = \frac{U}{d}
\]

Trong đó:

• \( E \): Cường độ điện trường.
• \( U \): Hiệu điện thế giữa hai bản của tụ điện hoặc hai điểm trong không gian.
• \( d \): Khoảng cách giữa hai bản hoặc giữa hai điểm.

Kết Luận

Hiểu biết về véctơ cường độ điện trường giúp chúng ta nắm rõ hơn về các hiện tượng điện từ và ứng dụng chúng trong cuộc sống hàng ngày. Từ việc phát triển các thiết bị công nghệ cao đến những ứng dụng trong y học và khoa học vũ trụ, cường độ điện trường đóng vai trò vô cùng quan trọng.

Cường độ điện trường là một đại lượng vectơ mô tả sự tác động của điện trường lên một điện tích thử tại một điểm cụ thể trong không gian. Vectơ cường độ điện trường có hướng và độ lớn, phụ thuộc vào điện tích gây ra điện trường và khoảng cách từ điện tích đó đến điểm đang xét.

Công thức cường độ điện trường \( \vec{E} \) được biểu diễn như sau:

\[
\vec{E} = \frac{\vec{F}}{q}
\]

• \( \vec{E} \): Vectơ cường độ điện trường tại điểm xét.
• \( \vec{F} \): Lực điện tác dụng lên điện tích thử \( q \).
• \( q \): Điện tích thử tại điểm đó.

Đối với điện tích điểm \( Q \), cường độ điện trường tại một điểm cách điện tích một khoảng cách \( r \) được tính như sau:

\[
E = k \cdot \frac{|Q|}{r^2}
\]

• \( E \): Cường độ điện trường (đơn vị: V/m).
• \( k \): Hằng số Coulomb, \( k \approx 8.99 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2 \).
• \( Q \): Điện tích gây ra điện trường.
• \( r \): Khoảng cách từ điện tích đến điểm đang xét.

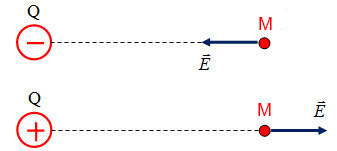
Cường độ điện trường có phương trùng với phương của lực điện tác dụng lên điện tích thử, và chiều của nó phụ thuộc vào dấu của điện tích gây ra điện trường:

1. Nếu \( Q > 0 \) (điện tích dương), vectơ cường độ điện trường có hướng ra xa điện tích.
2. Nếu \( Q < 0 \) (điện tích âm), vectơ cường độ điện trường có hướng về phía điện tích.

Đặc điểm của cường độ điện trường:

• Đơn vị của cường độ điện trường là Volt trên mét (V/m).
• Cường độ điện trường tỷ lệ thuận với điện tích \( Q \) và tỷ lệ nghịch với bình phương khoảng cách \( r \).
• Tại mỗi điểm trong điện trường, chỉ có một vectơ cường độ điện trường duy nhất.

Khái niệm cường độ điện trường giúp ta hiểu rõ hơn về các hiện tượng điện từ, như sự tương tác giữa các điện tích trong không gian và các ứng dụng thực tiễn như thiết kế các thiết bị điện tử và nghiên cứu vật lý học.

Cường độ điện trường của một điện tích điểm là một trong những trường hợp cơ bản nhất trong lý thuyết về điện trường. Điện tích điểm là một mô hình lý tưởng hóa, trong đó toàn bộ điện tích được giả sử tập trung tại một điểm duy nhất trong không gian. Vectơ cường độ điện trường tại một điểm gần điện tích điểm này có hướng, độ lớn phụ thuộc vào giá trị điện tích và khoảng cách từ điểm xét đến điện tích.

Công Thức Tính Cường Độ Điện Trường Của Điện Tích Điểm

Công thức tính cường độ điện trường \( \vec{E} \) của một điện tích điểm \( Q \) tại một điểm cách điện tích một khoảng cách \( r \) là:

\[
E = k \cdot \frac{|Q|}{r^2}
\]

Trong đó:

• \( E \): Cường độ điện trường tại điểm xét (đơn vị: V/m).
• \( k \): Hằng số Coulomb, \( k \approx 8.99 \times 10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2 \).
• \( Q \): Điện tích gây ra điện trường (đơn vị: Coulomb).
• \( r \): Khoảng cách từ điện tích đến điểm xét (đơn vị: mét).

Hướng Và Chiều Của Vectơ Cường Độ Điện Trường

Hướng và chiều của vectơ cường độ điện trường phụ thuộc vào dấu của điện tích điểm \( Q \):

1. Nếu \( Q > 0 \) (điện tích dương), vectơ cường độ điện trường sẽ có hướng ra xa khỏi điện tích.
2. Nếu \( Q < 0 \) (điện tích âm), vectơ cường độ điện trường sẽ có hướng về phía điện tích.

Đặc Điểm Của Cường Độ Điện Trường Của Điện Tích Điểm

• Cường độ điện trường tại một điểm trong không gian xung quanh điện tích điểm tỉ lệ thuận với độ lớn của điện tích \( Q \).
• Cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách từ điện tích đến điểm xét \( r \), nghĩa là khi khoảng cách tăng lên, cường độ điện trường giảm dần nhanh chóng.
• Vectơ cường độ điện trường luôn có phương thẳng đứng và trùng với đường nối từ điện tích đến điểm đang xét.

Ví Dụ Minh Họa

Xét một điện tích điểm dương \( Q = 2 \, \mu C \) (microcoulomb) đặt tại vị trí gốc tọa độ. Tính cường độ điện trường tại điểm cách điện tích này một khoảng \( r = 0.5 \, m \).

Sử dụng công thức tính cường độ điện trường:

\[
E = k \cdot \frac{|Q|}{r^2} = 8.99 \times 10^9 \cdot \frac{2 \times 10^{-6}}{(0.5)^2} = 7.192 \times 10^4 \, \text{V/m}
\]

Như vậy, tại khoảng cách 0.5 mét từ điện tích điểm, cường độ điện trường là \( 7.192 \times 10^4 \, V/m \).

Điện trường đều là một trường hợp đặc biệt của điện trường, trong đó vectơ cường độ điện trường có cùng độ lớn và cùng hướng tại mọi điểm trong không gian. Đây là một mô hình lý tưởng thường gặp trong các bài toán vật lý liên quan đến tụ điện hoặc các thiết bị tạo điện trường.

Đặc Điểm Của Điện Trường Đều

• Cường độ điện trường \( \vec{E} \) tại mọi điểm trong điện trường đều có cùng độ lớn và cùng hướng.
• Đường sức của điện trường đều là những đường thẳng song song và cách đều nhau.
• Điện trường đều thường được tạo ra giữa hai bản tụ điện phẳng song song mang điện tích trái dấu.

Công Thức Tính Cường Độ Điện Trường Đều

Giả sử chúng ta có hai bản tụ điện phẳng song song mang điện tích trái dấu, cách nhau một khoảng \( d \), diện tích của mỗi bản tụ là \( A \). Khi đó, cường độ điện trường đều giữa hai bản tụ điện được tính bằng công thức:

\[
E = \frac{\sigma}{\epsilon_0}
\]

Trong đó:

• \( E \): Cường độ điện trường giữa hai bản tụ (đơn vị: V/m).
• \( \sigma \): Mật độ điện tích trên mỗi bản tụ (đơn vị: C/m²).
• \( \epsilon_0 \): Hằng số điện môi của chân không, \( \epsilon_0 = 8.85 \times 10^{-12} \, \text{F/m} \).

Ứng Dụng Của Điện Trường Đều

1. Điện trường đều được sử dụng trong các tụ điện phẳng để lưu trữ năng lượng điện.
2. Trong các thí nghiệm vật lý, điện trường đều giúp nghiên cứu các hiện tượng điện và điện tử với sự phân bố đồng nhất của cường độ điện trường.
3. Điện trường đều còn được ứng dụng trong các thiết bị y tế, chẳng hạn như máy chụp cộng hưởng từ (MRI), nơi yêu cầu sự kiểm soát chính xác cường độ điện trường.

Ví Dụ Minh Họa

Xét một tụ điện phẳng song song với khoảng cách giữa hai bản là \( d = 0.02 \, m \), bản tụ có điện tích \( Q = 1 \times 10^{-6} \, C \) và diện tích của mỗi bản tụ là \( A = 0.1 \, m^2 \). Khi đó, mật độ điện tích \( \sigma \) được tính là:

\[
\sigma = \frac{Q}{A} = \frac{1 \times 10^{-6}}{0.1} = 1 \times 10^{-5} \, C/m^2
\]

Sau đó, cường độ điện trường đều giữa hai bản tụ là:

\[
E = \frac{\sigma}{\epsilon_0} = \frac{1 \times 10^{-5}}{8.85 \times 10^{-12}} \approx 1.13 \times 10^6 \, V/m
\]

Như vậy, cường độ điện trường giữa hai bản tụ là \( 1.13 \times 10^6 \, V/m \), và nó có cùng độ lớn và hướng tại mọi điểm giữa hai bản tụ.

Đường sức điện trường là các đường tưởng tượng trong không gian, dùng để mô tả hướng và độ mạnh yếu của điện trường tại các điểm khác nhau. Những đường này cung cấp một cách trực quan để hiểu được cách mà điện trường tác động lên các điện tích thử trong không gian.

Đặc Điểm Của Đường Sức Điện Trường

• Đường sức điện trường xuất phát từ các điện tích dương và kết thúc tại các điện tích âm, hoặc kéo dài vô hạn nếu không có điện tích âm để kết thúc.
• Đường sức không bao giờ cắt nhau, vì tại mỗi điểm trong không gian chỉ có một vectơ cường độ điện trường duy nhất.
• Độ dày (mật độ) của các đường sức điện trường biểu thị cường độ điện trường: nơi các đường sức dày hơn, cường độ điện trường mạnh hơn và ngược lại.

Hướng Của Đường Sức Điện Trường

1. Đối với điện tích điểm dương, các đường sức điện trường có hướng ra xa khỏi điện tích.
2. Đối với điện tích điểm âm, các đường sức điện trường có hướng về phía điện tích.

Các Loại Điện Trường Và Đường Sức

• Điện Trường Điểm: Đối với một điện tích điểm, các đường sức là những đường cong đối xứng tỏa ra từ điện tích, với cường độ điện trường giảm dần theo khoảng cách.
• Điện Trường Đều: Đối với điện trường đều, các đường sức là những đường thẳng song song và cách đều nhau, như đã thấy giữa hai bản tụ điện phẳng song song.

Biểu Diễn Toán Học

Giả sử điện tích \( Q \) đặt tại điểm \( O \), cường độ điện trường tại điểm \( M \) cách \( O \) một khoảng \( r \) được biểu diễn như sau:

\[
\vec{E} = k \cdot \frac{|Q|}{r^2} \cdot \hat{r}
\]

Trong đó:

• \( \vec{E} \): Vectơ cường độ điện trường tại điểm \( M \).
• \( k \): Hằng số Coulomb.
• \( |Q| \): Độ lớn của điện tích điểm.
• \( r \): Khoảng cách từ điện tích đến điểm đang xét.
• \( \hat{r} \): Vectơ đơn vị chỉ hướng từ điện tích đến điểm xét.

Ví Dụ Minh Họa Đường Sức Điện Trường

Xét một điện tích điểm dương \( Q = 1 \, \mu C \). Các đường sức sẽ xuất phát từ điện tích này và lan rộng ra xung quanh theo mọi hướng. Tại một khoảng cách \( r = 1 \, m \), cường độ điện trường sẽ được tính theo công thức và các đường sức sẽ tỏa ra từ điện tích theo hướng xa dần.

Những đường sức này sẽ giúp chúng ta hình dung được hướng và độ mạnh yếu của điện trường tại các điểm xung quanh điện tích.

Cường độ điện trường có vai trò quan trọng trong nhiều lĩnh vực thực tiễn, từ việc thiết kế các thiết bị điện tử đến những ứng dụng trong công nghệ y tế và khoa học vũ trụ.

5.1. Thiết Kế Và Phân Tích Các Thiết Bị Điện Tử

Cường độ điện trường giúp xác định khả năng hoạt động của các thiết bị điện tử như tụ điện, mạch điện tích hợp. Khi một điện tích được đặt trong điện trường, nó sẽ chịu một lực \( \vec{F} = q \cdot \vec{E} \), trong đó \( q \) là điện tích và \( \vec{E} \) là cường độ điện trường. Việc kiểm soát cường độ điện trường giúp các kỹ sư thiết kế tối ưu hiệu suất của thiết bị.

5.2. Sử Dụng Trong Công Nghệ Y Tế

Cường độ điện trường được ứng dụng trong nhiều công nghệ y tế, đặc biệt trong các thiết bị chẩn đoán và điều trị như máy MRI (Magnetic Resonance Imaging). Điện trường mạnh mẽ tạo ra từ các thiết bị này giúp phát hiện các bất thường trong cơ thể con người, góp phần nâng cao hiệu quả chẩn đoán bệnh.

5.3. Khám Phá Vũ Trụ Và Nghiên Cứu Khoa Học

Trong nghiên cứu vũ trụ, cường độ điện trường giúp xác định động lực học của các hạt trong không gian. Ví dụ, trong quá trình nghiên cứu bức xạ vũ trụ, cường độ điện trường được sử dụng để tính toán sự tương tác giữa các hạt điện tích và từ trường trong không gian, từ đó hiểu rõ hơn về nguồn gốc và tính chất của bức xạ vũ trụ.

Dưới đây là một số bài tập và câu hỏi trắc nghiệm giúp bạn củng cố kiến thức về cường độ điện trường. Hãy đảm bảo rằng bạn đã nắm vững lý thuyết trước khi bắt đầu giải các bài tập này.

6.1. Bài Tập Tính Toán Véctơ Cường Độ Điện Trường

1. Bài tập 1: Cho một điện tích điểm \( q = 5 \, \mu C \) đặt tại điểm \( A \). Tính cường độ điện trường tại điểm \( B \) cách \( A \) một khoảng \( r = 2 \, m \).

   Lời giải:

   Áp dụng công thức tính cường độ điện trường:
   \[
   E = k \cdot \frac{|q|}{r^2}
   \]
   với \( k = 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \), ta có:
   \[
   E = 9 \times 10^9 \times \frac{5 \times 10^{-6}}{(2)^2} = 11250 \, \text{V/m}
   \]

2. Bài tập 2: Một điện tích \( q_1 = -2 \, \mu C \) đặt tại điểm \( O \), và \( q_2 = 3 \, \mu C \) đặt cách \( O \) một khoảng \( d = 3 \, m \). Tính véctơ cường độ điện trường tổng hợp tại điểm \( P \) trên trục nối \( q_1 \) và \( q_2 \), cách \( q_1 \) một khoảng \( r_1 = 2 \, m \).

   Lời giải:

   Cường độ điện trường tại điểm \( P \) do \( q_1 \) gây ra là:
   \[
   E_1 = k \cdot \frac{|q_1|}{r_1^2}
   \]
   Cường độ điện trường tại điểm \( P \) do \( q_2 \) gây ra là:
   \[
   E_2 = k \cdot \frac{|q_2|}{r_2^2}
   \]
   Trong đó, \( r_2 = d - r_1 = 1 \, m \). Tổng hợp cường độ điện trường tại \( P \) là:
   \[
   E_{TP} = E_1 - E_2
   \]

6.2. Câu Hỏi Trắc Nghiệm Lý Thuyết

Những câu hỏi trắc nghiệm sau đây giúp bạn kiểm tra khả năng hiểu biết về cường độ điện trường:

• Câu 1: Cường độ điện trường tại một điểm trong điện trường được xác định bằng:
  1. Điện tích đặt tại điểm đó.
  2. Lực điện tác dụng lên một điện tích thử tại điểm đó.
  3. Khoảng cách từ điểm đó đến nguồn điện trường.
  4. Hằng số điện môi của môi trường.

  Đáp án: B

• Câu 2: Trong điện trường đều, các đường sức điện:
  1. Có hình dạng cong.
  2. Là những đường thẳng song song và cách đều.
  3. Hội tụ tại một điểm.
  4. Là những đường vòng tròn đồng tâm.

  Đáp án: B

6.3. Giải Bài Tập Nâng Cao Về Cường Độ Điện Trường

Các bài tập nâng cao yêu cầu bạn áp dụng kiến thức một cách linh hoạt và sáng tạo:

1. Bài tập 1: Hai điện tích \( q_1 \) và \( q_2 \) đặt tại hai điểm \( A \) và \( B \) trong không gian. Tìm vị trí điểm \( C \) trên đường thẳng \( AB \) sao cho cường độ điện trường tại \( C \) bằng 0.
2. Bài tập 2: Cho một mặt phẳng tích điện vô hạn với mật độ điện tích bề mặt \( \sigma \). Tính cường độ điện trường tại một điểm cách mặt phẳng một khoảng \( h \).