Chủ đề trong điện trường đều gọi vm và vn: "Trong điện trường đều gọi VM và VN" là một khái niệm quan trọng trong vật lý, giúp hiểu rõ hơn về điện thế và cường độ điện trường. Bài viết này sẽ cung cấp một cái nhìn tổng quan, từ lý thuyết cơ bản đến các ứng dụng và bài tập thực hành, giúp bạn nắm vững kiến thức một cách hiệu quả nhất.
Mục lục
Tìm hiểu về điện thế trong điện trường đều
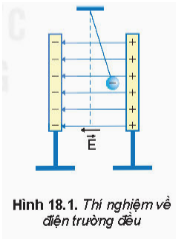
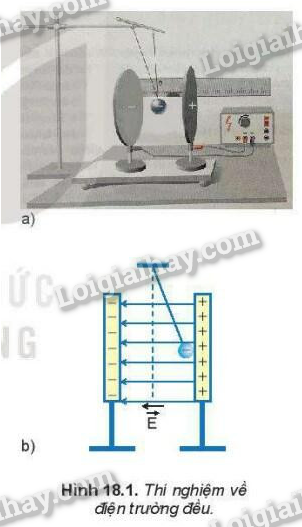
Trong vật lý, điện trường đều là một khái niệm quan trọng thường được giảng dạy ở bậc trung học phổ thông. Điện trường đều được định nghĩa là loại điện trường mà tại mọi điểm, cường độ điện trường đều có cùng phương, chiều và độ lớn. Điều này có nghĩa là các đường sức điện của điện trường đều là những đường thẳng song song và cách đều nhau.
Các khái niệm liên quan
- Điện thế \(V_M\) và \(V_N\): Đây là điện thế tại hai điểm \(M\) và \(N\) trong điện trường đều.
- Hiệu điện thế \(U_{MN}\): Đây là hiệu điện thế giữa hai điểm \(M\) và \(N\), được tính bằng công thức:
\[
U_{MN} = V_M - V_N
\]
Ứng dụng và ví dụ minh họa
Trong bài tập vật lý, các bạn học sinh thường gặp phải các câu hỏi liên quan đến việc tính toán điện thế và hiệu điện thế trong điện trường đều. Ví dụ, nếu biết hiệu điện thế giữa hai điểm và khoảng cách giữa chúng, ta có thể tính được cường độ điện trường \(E\) bằng công thức:
\[
E = \frac{U_{MN}}{d}
\]
Trong đó:
- \(E\) là cường độ điện trường.
- \(U_{MN}\) là hiệu điện thế giữa hai điểm \(M\) và \(N\).
- \(d\) là khoảng cách giữa hai điểm đó.
Quy luật và tính chất
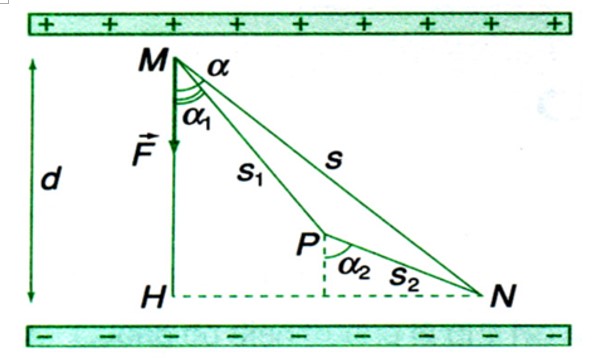
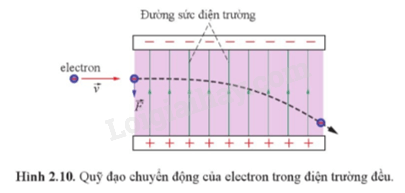
Khi một điện tích di chuyển trong điện trường đều theo phương vuông góc với các đường sức điện, vận tốc của điện tích sẽ thay đổi theo phương song song với đường sức, nhưng không thay đổi theo phương vuông góc với đường sức. Điều này dẫn đến quỹ đạo của điện tích trở thành một đường parabol.
Kết luận
Khái niệm về điện trường đều và cách tính toán các đại lượng liên quan như điện thế, hiệu điện thế là phần kiến thức quan trọng giúp học sinh hiểu rõ hơn về các hiện tượng vật lý liên quan đến điện từ.
.png)
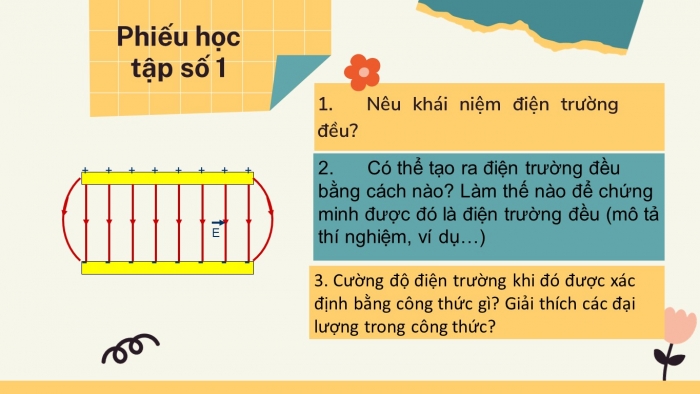
I. Khái niệm cơ bản về điện trường đều
Điện trường đều là một loại điện trường đặc biệt trong đó cường độ điện trường tại mọi điểm đều bằng nhau về độ lớn, cùng phương và cùng chiều. Điều này tạo ra một môi trường mà các đường sức điện là những đường thẳng song song và cách đều nhau.
- Định nghĩa: Điện trường đều là điện trường mà tại mọi điểm trong không gian, cường độ điện trường \(E\) có cùng giá trị và hướng. Điều này có nghĩa là nếu bạn đặt một điện tích thử tại bất kỳ điểm nào trong điện trường này, lực tác dụng lên nó sẽ có cùng độ lớn và phương hướng.
- Cường độ điện trường: Cường độ điện trường trong điện trường đều được xác định bằng công thức:
\[
E = \frac{U}{d}
\]
- Trong đó:
- \(E\) là cường độ điện trường.
- \(U\) là hiệu điện thế giữa hai điểm trong điện trường.
- \(d\) là khoảng cách giữa hai điểm đó.
- Đặc điểm: Các đường sức điện trong điện trường đều là những đường thẳng song song và cách đều nhau. Điều này thể hiện tính chất không đổi của cường độ điện trường trong suốt không gian của điện trường.
Điện trường đều thường gặp trong các bài toán liên quan đến tụ điện phẳng, nơi giữa hai bản tụ tạo ra một điện trường đều. Đây là cơ sở để hiểu các hiện tượng điện từ phức tạp hơn và áp dụng vào các lĩnh vực kỹ thuật và khoa học.
II. Điện thế tại các điểm trong điện trường
Điện thế là một đại lượng vật lý quan trọng trong việc mô tả trạng thái của một điểm trong điện trường. Trong điện trường đều, điện thế tại các điểm được xác định dựa trên mối quan hệ giữa cường độ điện trường và khoảng cách giữa các điểm trong không gian.
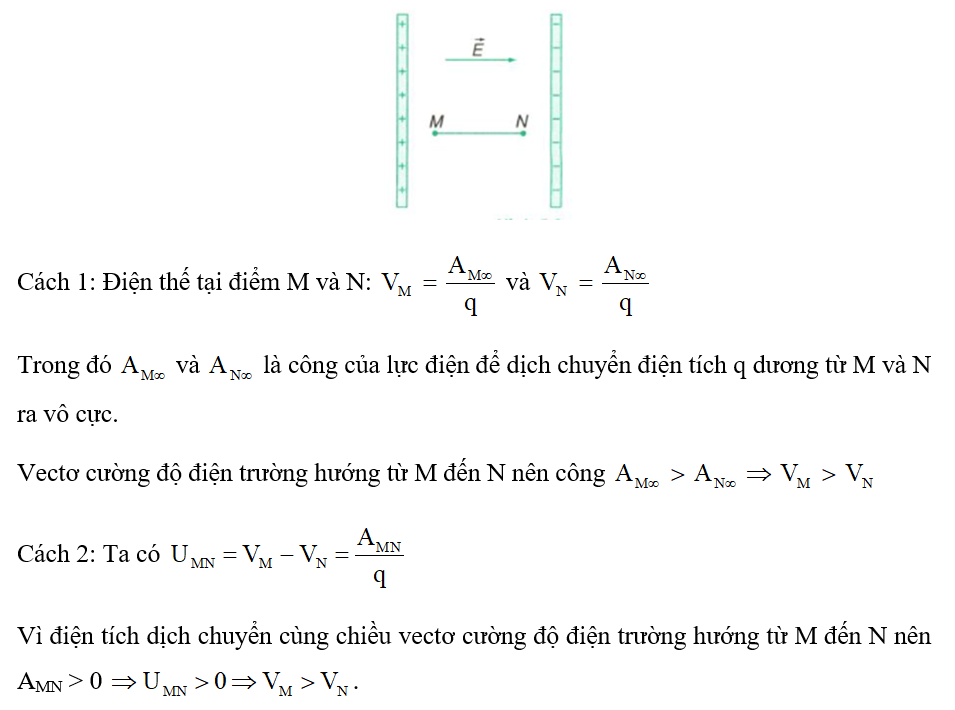
- Điện thế tại một điểm: Điện thế tại một điểm \(M\) trong điện trường đều được định nghĩa là công của lực điện tác dụng lên một điện tích dương đơn vị khi di chuyển điện tích đó từ điểm \(M\) đến điểm vô cực. Điện thế này được ký hiệu là \(V_M\).
- Hiệu điện thế giữa hai điểm: Hiệu điện thế giữa hai điểm \(M\) và \(N\) trong điện trường đều là sự chênh lệch điện thế giữa hai điểm đó, ký hiệu là \(U_{MN}\). Hiệu điện thế này được tính bằng công thức:
\[
U_{MN} = V_M - V_N
\]
- Mối liên hệ với cường độ điện trường: Trong điện trường đều, cường độ điện trường \(E\) có mối liên hệ trực tiếp với hiệu điện thế giữa hai điểm và khoảng cách giữa chúng, được biểu diễn bằng công thức:
\[
E = \frac{U_{MN}}{d}
\]
- Trong đó:
- \(E\) là cường độ điện trường.
- \(U_{MN}\) là hiệu điện thế giữa hai điểm \(M\) và \(N\).
- \(d\) là khoảng cách giữa hai điểm \(M\) và \(N\).
- Đặc điểm của điện thế trong điện trường đều: Trong điện trường đều, điện thế tại các điểm nằm trên cùng một mặt phẳng vuông góc với các đường sức điện sẽ bằng nhau. Điều này có nghĩa là mặt phẳng đó là một mặt đẳng thế.
Hiểu rõ khái niệm về điện thế tại các điểm trong điện trường đều giúp chúng ta nắm vững hơn về cách thức hoạt động của các thiết bị điện tử và ứng dụng thực tế trong kỹ thuật.

III. Ứng dụng và ví dụ minh họa
Điện trường đều có nhiều ứng dụng quan trọng trong thực tế và là nền tảng cho nhiều nguyên lý hoạt động của các thiết bị điện tử. Hiểu rõ cách điện trường đều hoạt động giúp chúng ta ứng dụng hiệu quả trong các lĩnh vực khác nhau.
- Ứng dụng trong tụ điện: Tụ điện phẳng là một ví dụ điển hình của điện trường đều. Giữa hai bản tụ điện song song, điện trường được xem là đều với cường độ không đổi. Điều này giúp cho tụ điện có khả năng lưu trữ năng lượng điện một cách ổn định.
- Ứng dụng trong phân tích tín hiệu: Trong các hệ thống truyền tín hiệu, điện trường đều được sử dụng để duy trì sự ổn định của tín hiệu điện, giảm thiểu nhiễu và mất mát năng lượng. Điều này rất quan trọng trong việc truyền dẫn thông tin qua các dây dẫn và mạch điện.
- Ứng dụng trong cảm biến và đo lường: Các cảm biến điện trường sử dụng nguyên lý điện trường đều để đo lường các đại lượng vật lý như điện áp, điện tích, và cường độ điện trường. Điều này giúp tăng độ chính xác và hiệu quả trong các thiết bị đo lường.
Dưới đây là một ví dụ minh họa cụ thể về cách tính toán trong điện trường đều:
- Giả sử ta có hai điểm \(M\) và \(N\) trong một điện trường đều với cường độ \(E = 500 \, \text{V/m}\) và khoảng cách giữa hai điểm là \(d = 0.1 \, \text{m}\). Hiệu điện thế giữa hai điểm được tính bằng công thức:
\[
U_{MN} = E \times d = 500 \times 0.1 = 50 \, \text{V}
\]
Ví dụ trên minh họa cách áp dụng công thức cường độ điện trường để tính hiệu điện thế giữa hai điểm trong điện trường đều, một kỹ năng quan trọng trong việc giải quyết các bài toán thực tế.
XEM THÊM:
IV. Quy luật và tính chất liên quan
Trong điện trường đều, các quy luật và tính chất của điện trường có vai trò quan trọng trong việc hiểu rõ các hiện tượng vật lý cũng như ứng dụng vào thực tế. Dưới đây là một số quy luật và tính chất liên quan.
- Quy luật bảo toàn năng lượng: Trong một điện trường đều, năng lượng điện của một điện tích di chuyển giữa hai điểm phụ thuộc vào hiệu điện thế giữa hai điểm đó. Công của lực điện di chuyển điện tích từ điểm \(M\) đến \(N\) trong điện trường đều không phụ thuộc vào đường đi mà chỉ phụ thuộc vào vị trí ban đầu và cuối cùng của điện tích.
- Định luật Coulomb: Trong điện trường đều, lực tác dụng giữa hai điện tích điểm tỉ lệ thuận với tích của độ lớn hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Định luật này cũng có thể áp dụng để hiểu sự tương tác giữa các điện tích trong điện trường đều.
- Tính chất đẳng thế: Các mặt phẳng vuông góc với các đường sức điện trong điện trường đều là các mặt đẳng thế, nơi mà điện thế tại mọi điểm trên mặt phẳng đó đều bằng nhau. Điều này có nghĩa là không có công nào được thực hiện khi di chuyển một điện tích dọc theo một mặt đẳng thế.
- Tính chất đường sức điện: Trong điện trường đều, các đường sức điện là những đường thẳng song song và cách đều nhau. Điều này biểu thị rằng cường độ điện trường tại mọi điểm trong không gian đều là không đổi. Các đường sức này luôn đi từ vùng có điện thế cao đến vùng có điện thế thấp.
Những quy luật và tính chất này không chỉ giúp chúng ta hiểu rõ hơn về bản chất của điện trường đều mà còn cung cấp nền tảng lý thuyết vững chắc để giải quyết các bài toán điện học và áp dụng vào các công nghệ hiện đại.