Công Thức Tính Cường Độ Điện Trường: Hướng Dẫn Chi Tiết Và Ứng Dụng Thực Tiễn

Cường độ điện trường là đại lượng mô tả độ mạnh yếu của điện trường tại một điểm trong không gian. Nó được xác định bằng công thức:

\[
\vec{E} = \frac{\vec{F}}{q}
\]

Trong đó:

• \(\vec{E}\): Cường độ điện trường (V/m)
• \(\vec{F}\): Lực điện tác dụng lên điện tích thử (N)
• \(q\): Độ lớn của điện tích thử (C)

Ngoài ra, đối với một điện tích điểm \(Q\) tại điểm cách \(r\) từ điện tích đó, cường độ điện trường còn được tính bằng công thức:

\[
E = k \cdot \frac{|Q|}{r^2}
\]

Trong đó:

• \(E\): Cường độ điện trường (V/m)
• \(k\): Hằng số điện môi (\(k \approx 9 \times 10^9 \, \text{Nm}^2/\text{C}^2\))
• \(Q\): Điện tích tạo ra điện trường (C)
• \(r\): Khoảng cách từ điện tích đến điểm cần tính cường độ điện trường (m)

Ứng Dụng Của Công Thức Tính Cường Độ Điện Trường

Công thức này có nhiều ứng dụng trong việc giải các bài toán về điện trường trong môn Vật lý, giúp học sinh và sinh viên hiểu rõ hơn về tương tác điện từ và các hiện tượng vật lý liên quan.

Lưu Ý Khi Sử Dụng Công Thức

Khi áp dụng công thức tính cường độ điện trường, cần chú ý đến các yếu tố như giá trị điện tích, khoảng cách, và hướng của lực điện để có kết quả chính xác. Đồng thời, cần hiểu rõ bản chất của điện trường và cách thức nó tương tác với các vật thể trong không gian.

Cường độ điện trường là một đại lượng vật lý đặc trưng cho độ mạnh yếu của điện trường tại một điểm trong không gian. Điện trường là một trường lực bao quanh các hạt mang điện và tác dụng lực lên các hạt khác có điện tích trong vùng không gian đó.

Cường độ điện trường tại một điểm được định nghĩa là lực điện \(\vec{F}\) tác dụng lên một đơn vị điện tích dương thử \(q\) đặt tại điểm đó:

\[
\vec{E} = \frac{\vec{F}}{q}
\]

Trong đó:

• \(\vec{E}\) là cường độ điện trường (đơn vị: V/m).
• \(\vec{F}\) là lực điện tác dụng lên điện tích thử (đơn vị: N).
• \(q\) là độ lớn của điện tích thử (đơn vị: C).

Cường độ điện trường là một đại lượng vectơ, có hướng trùng với hướng của lực điện tác dụng lên một điện tích dương thử. Độ lớn của cường độ điện trường biểu thị độ mạnh của điện trường tại điểm đó, và hướng của nó cho biết hướng lực điện tác dụng lên điện tích dương.

Đặc biệt, trong trường hợp điện trường do một điện tích điểm \(Q\) sinh ra tại khoảng cách \(r\) từ điện tích đó, cường độ điện trường có thể được tính bằng công thức:

\[
E = k \cdot \frac{|Q|}{r^2}
\]

Trong đó:

• \(k\) là hằng số điện môi trong chân không, có giá trị xấp xỉ \(9 \times 10^9 \, \text{Nm}^2/\text{C}^2\).
• \(Q\) là điện tích tạo ra điện trường (đơn vị: C).
• \(r\) là khoảng cách từ điện tích đến điểm đang xét (đơn vị: m).

Công thức này cho thấy cường độ điện trường tỉ lệ thuận với điện tích nguồn \(Q\) và tỉ lệ nghịch với bình phương khoảng cách \(r\), điều này có nghĩa là khi khoảng cách tăng lên, cường độ điện trường sẽ giảm đi nhanh chóng.

Cường độ điện trường là một đại lượng quan trọng trong việc mô tả điện trường tại một điểm bất kỳ. Để tính toán cường độ điện trường, ta có các công thức cụ thể tùy thuộc vào tình huống và cấu hình của điện trường.

2.1. Công Thức Tổng Quát

Công thức tổng quát để tính cường độ điện trường tại một điểm, do lực điện \(\vec{F}\) tác dụng lên điện tích thử \(q\) tạo ra, được biểu diễn như sau:

\[
\vec{E} = \frac{\vec{F}}{q}
\]

Trong đó:

• \(\vec{E}\): Cường độ điện trường (V/m).
• \(\vec{F}\): Lực điện tác dụng lên điện tích thử (N).
• \(q\): Điện tích thử (C).

2.2. Công Thức Đối Với Điện Tích Điểm

Đối với một điện tích điểm \(Q\), cường độ điện trường tại một điểm cách điện tích đó một khoảng cách \(r\) được tính bằng công thức:

\[
E = k \cdot \frac{|Q|}{r^2}
\]

Trong đó:

• \(E\): Cường độ điện trường tại điểm cần tính (V/m).
• \(k\): Hằng số điện môi trong chân không, có giá trị xấp xỉ \(9 \times 10^9 \, \text{Nm}^2/\text{C}^2\).
• \(Q\): Điện tích điểm tạo ra điện trường (C).
• \(r\): Khoảng cách từ điện tích điểm đến điểm cần tính (m).

2.3. Công Thức Trong Trường Hợp Đặc Biệt

Một số trường hợp đặc biệt của cường độ điện trường bao gồm:

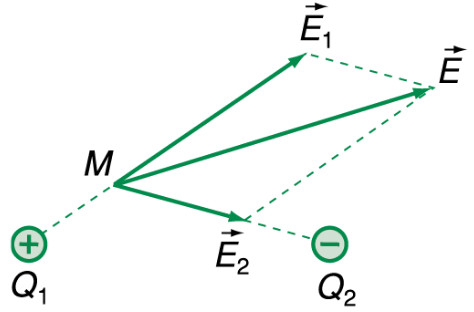
• Điện trường do một hệ điện tích tạo ra: Cường độ điện trường tổng hợp tại một điểm là tổng vectơ của các cường độ điện trường do từng điện tích trong hệ tạo ra.
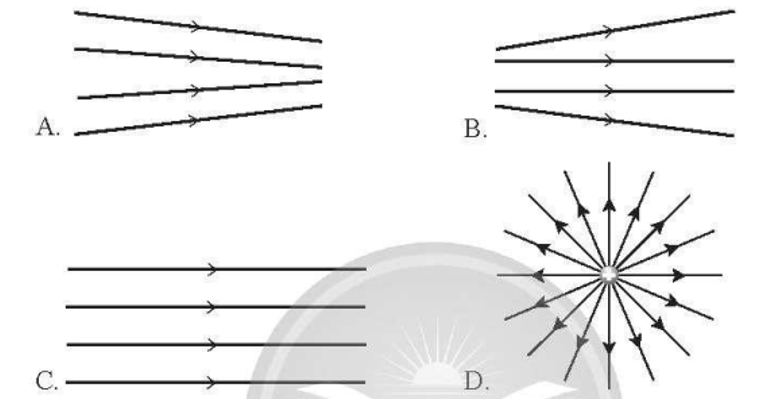
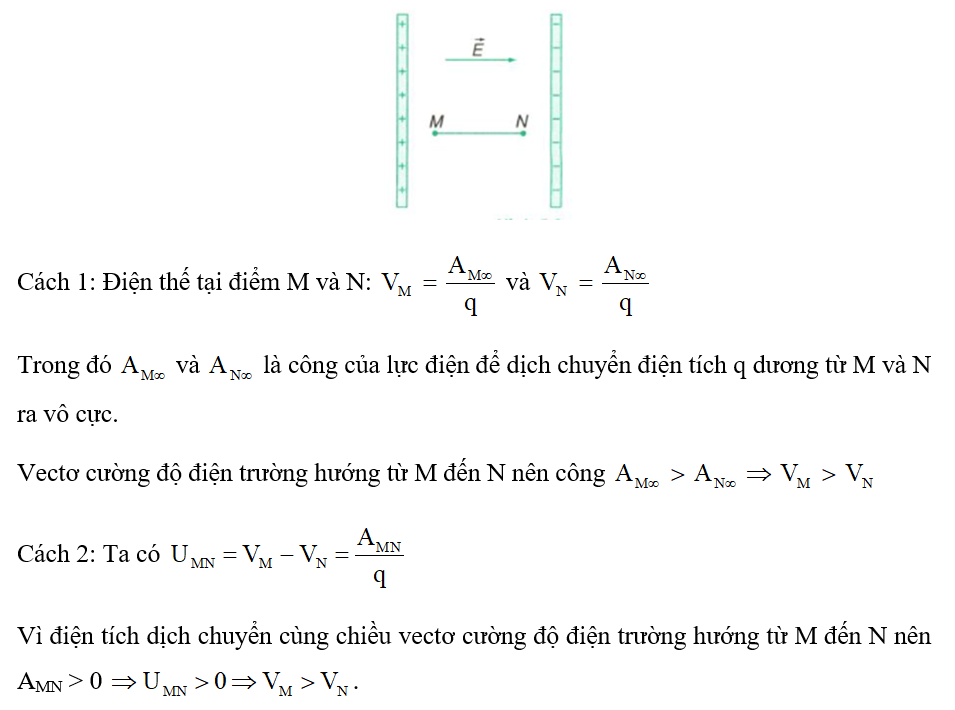
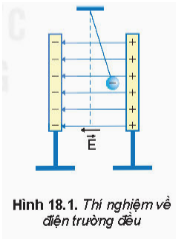
• Điện trường đều: Trong một điện trường đều, cường độ điện trường tại mọi điểm có cùng độ lớn và hướng, và được tính bằng công thức:

  \[ E = \frac{U}{d} \]

  • \(E\): Cường độ điện trường đều (V/m).
  • \(U\): Hiệu điện thế giữa hai bản cực (V).
  • \(d\): Khoảng cách giữa hai bản cực (m).

Những công thức trên giúp ta hiểu rõ cách tính và ứng dụng cường độ điện trường trong các bài toán vật lý khác nhau, từ các tình huống cơ bản đến phức tạp.

Cường độ điện trường (E) là một khái niệm quan trọng trong Vật lý, không chỉ giúp chúng ta hiểu về tác động của điện trường mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực khác nhau. Dưới đây là một số ứng dụng tiêu biểu của cường độ điện trường:

3.1. Ứng dụng trong bài toán điện trường

Trong các bài toán về điện trường, cường độ điện trường được sử dụng để xác định lực tác dụng lên các điện tích trong một không gian nhất định. Bằng cách sử dụng các công thức tính toán như \( E = \frac{F}{q} \) hoặc \( E = k \frac{Q}{r^2} \), ta có thể tính toán và phân tích các tình huống phức tạp liên quan đến nhiều nguồn điện tích, từ đó đưa ra các dự đoán chính xác về tương tác lực trong hệ thống điện trường.

3.2. Ứng dụng trong các thiết bị điện

Cường độ điện trường có vai trò quan trọng trong thiết kế và vận hành các thiết bị điện và điện tử. Ví dụ, trong các linh kiện bán dẫn như diode và transistor, điện trường nội bộ giúp điều khiển dòng điện và điện áp. Hơn nữa, trong các máy gia tốc hạt, cường độ điện trường cao được sử dụng để gia tốc các hạt đến vận tốc gần bằng vận tốc ánh sáng, hỗ trợ các thí nghiệm vật lý hạt nhân và khám phá các hạt cơ bản.

3.3. Vai trò của cường độ điện trường trong nghiên cứu và công nghệ

Trong lĩnh vực y tế, cường độ điện trường được ứng dụng trong các thiết bị chẩn đoán và điều trị như máy MRI và các phương pháp điều trị bằng điện trường để chữa bệnh. Ngoài ra, cường độ điện trường còn giúp phân tích các hiện tượng vật lý trong nghiên cứu khoa học, từ đó phát triển các công nghệ mới, như các vật liệu siêu dẫn hoặc các hệ thống lưu trữ năng lượng tiên tiến.

Các ứng dụng trên cho thấy vai trò đa dạng và quan trọng của cường độ điện trường trong cả nghiên cứu khoa học và các ngành công nghiệp khác nhau. Việc hiểu và vận dụng đúng các nguyên lý của cường độ điện trường sẽ tiếp tục mở ra nhiều tiềm năng phát triển mới trong tương lai.

Để giải quyết các bài tập liên quan đến cường độ điện trường, học sinh cần tuân theo các bước cơ bản dưới đây. Mỗi bước cần được thực hiện cẩn thận và chính xác để đảm bảo kết quả chính xác.

4.1. Các bước cơ bản

1. Xác định đối tượng và điều kiện bài toán:

   Xác định rõ ràng các điện tích, vị trí của chúng và môi trường trong bài toán. Điều này giúp hình dung các vectơ cường độ điện trường và hướng đi của chúng.

2. Tính cường độ điện trường tại một điểm:

   Sử dụng công thức tổng quát của cường độ điện trường:
   \[
   E = k \cdot \frac{|Q|}{r^2}
   \]
   Trong đó:
   

   
   
   • \(E\) là cường độ điện trường (V/m)
   
   
   • \(k\) là hằng số điện (k = 9 \times 10^9 \, \text{Nm}^2/\text{C}^2)
   
   
   • \(Q\) là điện tích gây ra điện trường (C)
   
   
   • \(r\) là khoảng cách từ điện tích đến điểm cần tính (m)
   
   
   
   


3. Xác định phương và chiều của vectơ cường độ điện trường:

   Vẽ các vectơ cường độ điện trường do các điện tích gây ra tại điểm cần tính. Nếu có nhiều điện tích, cần xác định tổng hợp các vectơ này theo quy tắc hình bình hành hoặc quy tắc cộng vectơ.

4. Tính toán cường độ điện trường tổng hợp:

   Tổng hợp các thành phần vectơ để tìm ra cường độ điện trường tổng hợp tại điểm đó, sử dụng các công thức vector và hình học.

5. Kiểm tra và kết luận:

   So sánh kết quả với các điều kiện ban đầu của bài toán để đảm bảo tính chính xác. Đừng quên đánh giá ý nghĩa của kết quả thu được.

4.2. Lưu ý khi tính toán

• Đảm bảo rằng tất cả các giá trị được sử dụng trong cùng một hệ đơn vị (SI) để tránh sai sót.
• Kiểm tra kỹ các hướng và dấu của các vectơ cường độ điện trường, đặc biệt khi tổng hợp các vectơ.
• Nếu có nhiều điện tích, hãy phân chia rõ ràng các thành phần vectơ theo trục để dễ dàng trong việc tổng hợp.

4.3. Các ví dụ minh họa

Dưới đây là một ví dụ minh họa cụ thể:

Bài tập: Một điện tích \(q = 10^{-7}C\) đặt tại điểm M trong điện trường của một điện tích điểm \(Q\), chịu tác dụng của lực \(F = 3 \times 10^{-3}N\). Hãy tính cường độ điện trường tại điểm M.

Hướng dẫn:

• Áp dụng công thức: \[ E = \frac{F}{q} \] Với \(F = 3 \times 10^{-3}N\) và \(q = 10^{-7}C\), ta tính được \(E\).

Qua đó, cường độ điện trường tại điểm M là \(E = 3 \times 10^{4} V/m\).

Việc sử dụng công thức tính cường độ điện trường đòi hỏi sự chính xác cao và hiểu biết đầy đủ về các yếu tố liên quan. Dưới đây là một số lưu ý quan trọng khi áp dụng công thức này trong các bài toán và thực tiễn.

5.1. Những sai lầm thường gặp

• Không xét đến ảnh hưởng của các yếu tố bên ngoài: Khi tính toán cường độ điện trường, thường bỏ qua các yếu tố như môi trường xung quanh, vật liệu điện môi, hay sự hiện diện của các điện tích khác có thể dẫn đến kết quả sai lệch.
• Nhầm lẫn giữa các đơn vị đo: Đơn vị đo cường độ điện trường là Volt trên mét (V/m). Việc nhầm lẫn đơn vị đo có thể dẫn đến sai số nghiêm trọng trong kết quả tính toán.
• Áp dụng sai công thức: Đối với các trường hợp đặc biệt như điện tích điểm, hoặc trong môi trường khác nhau (chẳng hạn như môi trường không đồng nhất), cần áp dụng đúng công thức để tính toán chính xác.

5.2. Cách khắc phục lỗi khi tính toán

1. Kiểm tra lại các điều kiện biên: Trước khi áp dụng công thức, hãy chắc chắn rằng bạn đã xét đến tất cả các điều kiện biên và yếu tố ảnh hưởng để đảm bảo tính chính xác của kết quả.
2. Sử dụng đúng công thức và đơn vị đo: Luôn kiểm tra kỹ công thức trước khi tính toán, đặc biệt chú ý đến các đơn vị đo lường để tránh nhầm lẫn.
3. Áp dụng phương pháp kiểm tra chéo: Sau khi có kết quả, hãy thử áp dụng phương pháp kiểm tra chéo hoặc sử dụng các công thức khác để xác minh lại tính chính xác của kết quả.

Bằng cách chú ý đến các yếu tố trên, bạn có thể giảm thiểu các sai sót trong quá trình tính toán cường độ điện trường, từ đó đạt được kết quả chính xác và đáng tin cậy hơn.