Chủ đề công thức chuyển động ném ngang ném xiên: Chào mừng bạn đến với hướng dẫn chi tiết về công thức chuyển động ném ngang và ném xiên! Bài viết này sẽ cung cấp cái nhìn sâu sắc về các khái niệm cơ bản, công thức toán học và ứng dụng thực tế của hai loại chuyển động này. Dù bạn là học sinh, sinh viên hay người đam mê vật lý, đây là nguồn tài liệu hữu ích giúp bạn nắm vững kiến thức và áp dụng vào các tình huống thực tế.
Mục lục
Công thức chuyển động ném ngang và ném xiên
Chuyển động ném ngang và ném xiên là các khái niệm cơ bản trong vật lý, liên quan đến chuyển động của vật thể trong không gian. Dưới đây là tổng hợp các công thức và giải thích chi tiết về các loại chuyển động này:
Chuyển động ném ngang
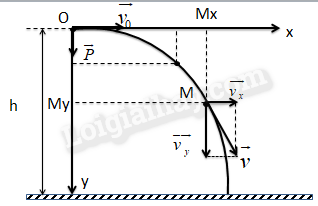
Chuyển động ném ngang là chuyển động của vật thể khi nó được ném ngang với một vận tốc ban đầu. Các yếu tố chính của chuyển động này bao gồm:
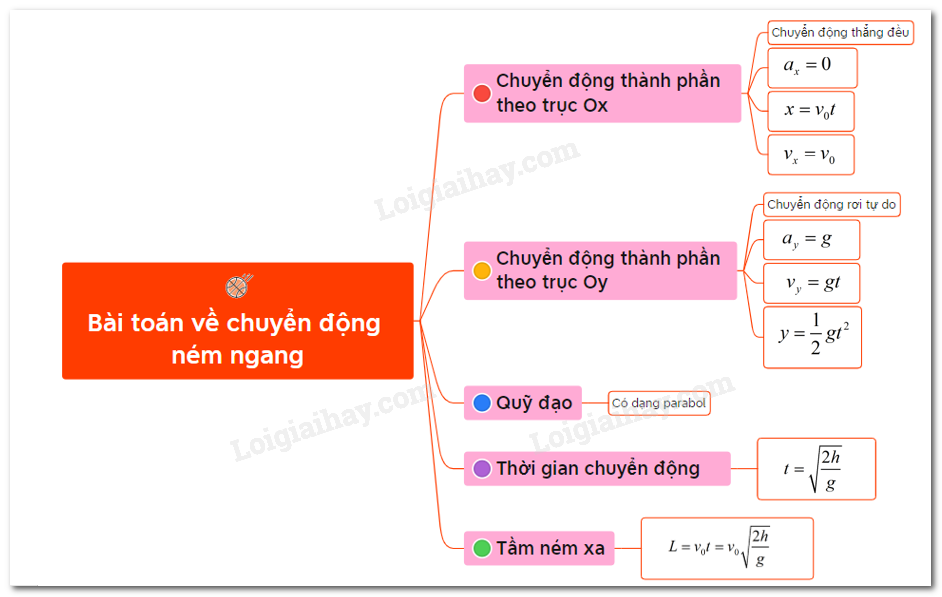
- Vận tốc ngang (\( v_x \)): Vận tốc này là không đổi trong suốt quá trình chuyển động.
- Vận tốc rơi tự do (\( v_y \)): Vận tốc này tăng dần theo thời gian do ảnh hưởng của trọng lực.
- Khoảng cách ngang (\( x \)): Được tính bằng công thức \( x = v_x \cdot t \), trong đó \( t \) là thời gian.
- Chiều cao rơi (\( y \)): Được tính bằng công thức \( y = \frac{1}{2} g t^2 \), trong đó \( g \) là gia tốc trọng trường (khoảng 9.8 m/s²).
Công thức chuyển động ném ngang
Vận tốc ngang và chiều cao rơi của vật thể trong chuyển động ném ngang được mô tả bằng các công thức sau:
x = v_x \cdot t
y = \frac{1}{2} g t^2
Chuyển động ném xiên
Chuyển động ném xiên xảy ra khi một vật thể được ném với một góc so với phương nằm ngang. Các yếu tố chính của chuyển động này bao gồm:
- Vận tốc ban đầu (\( v_0 \)): Vận tốc này có thể phân tách thành hai thành phần: ngang và dọc.
- Thành phần vận tốc ngang (\( v_{0x} \)): Được tính bằng công thức \( v_{0x} = v_0 \cdot \cos(\theta) \), trong đó \( \theta \) là góc ném.
- Thành phần vận tốc dọc (\( v_{0y} \)): Được tính bằng công thức \( v_{0y} = v_0 \cdot \sin(\theta) \).
- Thời gian lên cao (T): Được tính bằng công thức \( T = \frac{v_{0y}}{g} \).
- Chiều cao tối đa (H): Được tính bằng công thức \( H = \frac{v_{0y}^2}{2g} \).
- Khoảng cách xa nhất (\( R \)): Được tính bằng công thức \( R = \frac{v_0^2 \cdot \sin(2\theta)}{g} \).
Công thức chuyển động ném xiên
Các công thức cơ bản của chuyển động ném xiên được trình bày như sau:
v_{0x} = v_0 \cdot \cos(\theta)
v_{0y} = v_0 \cdot \sin(\theta)
T = \frac{v_{0y}}{g}
H = \frac{v_{0y}^2}{2g}
R = \frac{v_0^2 \cdot \sin(2\theta)}{g}
Các công thức trên giúp chúng ta hiểu rõ hơn về chuyển động của vật thể trong không gian, đặc biệt là khi chúng ta nghiên cứu các hiện tượng vật lý và áp dụng chúng vào các bài toán thực tế.

.png)
Tổng Quan Về Chuyển Động Ném Ngang
Chuyển động ném ngang là một dạng chuyển động của vật thể được ném theo phương nằm ngang dưới tác dụng của trọng lực. Đặc điểm của chuyển động này là có tốc độ ngang không thay đổi và vận tốc theo phương thẳng đứng bị gia tốc đều do trọng lực.
Khái Niệm Cơ Bản
Chuyển động ném ngang bao gồm hai thành phần chuyển động độc lập: chuyển động theo phương ngang với vận tốc không đổi và chuyển động theo phương thẳng đứng với gia tốc đều do trọng lực. Vận tốc ngang (vx) không thay đổi, trong khi vận tốc dọc (vy) thay đổi theo thời gian.
Các Công Thức Chính
- Thời gian bay: \( t = \frac{2h}{g} \)
- Khoảng cách ngang: \( x = v_x \cdot t \)
- Chiều cao tối đa: \( h = \frac{v_y^2}{2g} \)
Trong đó:
- \( v_x \) là vận tốc ngang của vật
- \( v_y \) là vận tốc dọc của vật
- \( g \) là gia tốc trọng trường (khoảng 9.8 m/s²)
- \( h \) là chiều cao mà vật đạt được
Ứng Dụng Trong Thực Tế
Chuyển động ném ngang thường được áp dụng trong các tình huống thực tế như thể thao (bóng chày, bóng rổ), thiết kế trò chơi video, và trong các bài toán vật lý để tính toán các yếu tố như khoảng cách và thời gian.
Tổng Quan Về Chuyển Động Ném Xiên
Chuyển động ném xiên là một loại chuyển động phức tạp hơn so với ném ngang, khi vật thể được ném theo một góc so với mặt đất, dẫn đến sự kết hợp giữa chuyển động ngang và chuyển động dọc. Trong chuyển động ném xiên, cả hai thành phần chuyển động đều ảnh hưởng đến quỹ đạo của vật thể.
Khái Niệm Cơ Bản
Chuyển động ném xiên bao gồm hai thành phần chính: chuyển động ngang với vận tốc không đổi và chuyển động dọc với gia tốc đều do trọng lực. Góc ném ảnh hưởng đến quỹ đạo của vật thể, khiến cho chuyển động trở nên phức tạp hơn.
Các Công Thức Chính
- Thời gian bay: \( t = \frac{2 v_0 \sin(\theta)}{g} \)
- Khoảng cách ngang: \( x = v_0 \cos(\theta) \cdot t \)
- Chiều cao tối đa: \( h = \frac{v_0^2 \sin^2(\theta)}{2g} \)
- Quỹ đạo: \( y = x \tan(\theta) - \frac{g x^2}{2 v_0^2 \cos^2(\theta)} \)
Trong đó:
- \( v_0 \) là vận tốc ném ban đầu
- \( \theta \) là góc ném
- \( g \) là gia tốc trọng trường (khoảng 9.8 m/s²)
- \( x \) là khoảng cách ngang
- \( y \) là chiều cao tại khoảng cách ngang \( x \)
Ứng Dụng Trong Thực Tế
Chuyển động ném xiên được ứng dụng rộng rãi trong các lĩnh vực như thiết kế đường đạn của tên lửa, phân tích các môn thể thao như bóng chày và bóng rổ, cũng như trong các bài toán vật lý trong trường học để hiểu rõ hơn về chuyển động và lực tác dụng.

So Sánh Giữa Ném Ngang và Ném Xiên
Chuyển động ném ngang và ném xiên là hai loại chuyển động quan trọng trong vật lý, mỗi loại có đặc điểm và ứng dụng riêng. Dưới đây là sự so sánh chi tiết giữa chúng:
Điểm Khác Biệt Chính
| Yếu Tố | Ném Ngang | Ném Xiên |
|---|---|---|
| Góc Ném | 0 độ (nằm ngang) | Khác 0 độ (theo góc α) |
| Vận Tốc Ngang | Không đổi | Biến đổi theo thời gian |
| Vận Tốc Dọc | Chỉ bị tác động bởi trọng lực | Có gia tốc đều do trọng lực |
| Quỹ Đạo | Đường thẳng ngang | Parabol |
| Thời Gian Bay | Thời gian bay phụ thuộc vào chiều cao rơi | Thời gian bay phụ thuộc vào góc ném và vận tốc |
Ứng Dụng và Tình Huống Thực Tế
- Ném Ngang: Thích hợp cho các tình huống có chiều cao không thay đổi nhiều, như ném bóng qua một lỗ hoặc thiết kế mô hình đơn giản.
- Ném Xiên: Áp dụng trong các tình huống thực tế như bóng chày, bóng rổ, và khi tính toán quỹ đạo của các tên lửa, đạn dược.

Ví Dụ Minh Họa
Ví Dụ Về Ném Ngang
Giả sử bạn ném một viên đá từ độ cao 10 mét với vận tốc ngang là 20 m/s. Để tính toán khoảng cách mà viên đá bay được, ta sử dụng công thức sau:
Thời gian viên đá rơi xuống đất có thể được tính bằng công thức:
\[
t = \sqrt{\frac{2h}{g}}
\]
Trong đó, \( h \) là độ cao (10 m) và \( g \) là gia tốc trọng trường (9.8 m/s²). Vậy thời gian rơi là:
\[
t = \sqrt{\frac{2 \times 10}{9.8}} \approx 1.43 \text{ giây}
\]
Khoảng cách ném ngang được tính bằng công thức:
\[
d = v \times t
\]
Với \( v \) là vận tốc ngang (20 m/s), ta có:
\[
d = 20 \times 1.43 \approx 28.6 \text{ mét}
\]
Vậy viên đá sẽ bay được khoảng 28.6 mét trước khi rơi xuống đất.
Ví Dụ Về Ném Xiên
Giả sử bạn ném một quả bóng với vận tốc 30 m/s và góc ném là 45 độ. Để tính toán khoảng cách tối đa mà quả bóng có thể bay được, ta sử dụng công thức:
Khoảng cách tối đa (hay còn gọi là tầm xa) được tính bằng công thức:
\[
R = \frac{v^2 \sin(2\theta)}{g}
\]
Trong đó, \( v \) là vận tốc ném (30 m/s), \( \theta \) là góc ném (45 độ), và \( g \) là gia tốc trọng trường (9.8 m/s²). Vì \( \sin(90^\circ) = 1 \), ta có:
\[
R = \frac{30^2 \times 1}{9.8} \approx 91.8 \text{ mét}
\]
Vậy quả bóng có thể bay được khoảng 91.8 mét.

Các Bài Tập Thực Hành
Bài Tập Cơ Bản
-
Giả sử bạn ném một viên đá với vận tốc ngang 15 m/s từ một độ cao 5 mét. Tính khoảng cách mà viên đá bay được trước khi rơi xuống đất.
Thực hiện theo các bước sau:
- Tính thời gian viên đá rơi xuống đất bằng công thức:
- Thay giá trị vào công thức:
- Tính khoảng cách ném ngang:
- Thay giá trị vào công thức:
\[
t = \sqrt{\frac{2h}{g}}
\]\[
t = \sqrt{\frac{2 \times 5}{9.8}} \approx 1.01 \text{ giây}
\]\[
d = v \times t
\]\[
d = 15 \times 1.01 \approx 15.2 \text{ mét}
\] -
Tính thời gian viên đá rơi xuống đất nếu bạn ném viên đá với vận tốc ngang 25 m/s từ độ cao 8 mét.
Thực hiện theo các bước sau:
- Tính thời gian rơi:
- Thay giá trị vào công thức:
\[
t = \sqrt{\frac{2h}{g}}
\]\[
t = \sqrt{\frac{2 \times 8}{9.8}} \approx 1.28 \text{ giây}
\]
Bài Tập Nâng Cao
-
Giả sử bạn ném một quả bóng với vận tốc 20 m/s và góc ném 30 độ. Tính tầm xa của quả bóng.
Thực hiện theo các bước sau:
- Tính khoảng cách tối đa bằng công thức:
- Chuyển góc ném thành radian và thay vào công thức:
\[
R = \frac{v^2 \sin(2\theta)}{g}
\]\[
\theta = 30^\circ = \frac{\pi}{6} \text{ radian}
\]\[
R = \frac{20^2 \times \sin\left(\frac{\pi}{3}\right)}{9.8} \approx 40.8 \text{ mét}
\] -
Tính tầm xa của một vật ném với vận tốc 25 m/s và góc ném 60 độ.
Thực hiện theo các bước sau:
- Tính khoảng cách tối đa:
- Thay vào công thức:
\[
R = \frac{25^2 \sin(2 \times 60^\circ)}{9.8}
\]\[
R = \frac{25^2 \times \sin(120^\circ)}{9.8} \approx 63.7 \text{ mét}
\]