Chủ đề lý thuyết chuyển động ném ngang: Khám phá lý thuyết chuyển động ném ngang từ cơ bản đến nâng cao trong bài viết này. Tìm hiểu về các thành phần chính, công thức quan trọng và ứng dụng thực tiễn của chuyển động ném ngang. Đây là nguồn tài liệu hoàn hảo để nắm vững kiến thức và áp dụng vào thực tế.
Mục lục
- Lý Thuyết Chuyển Động Ném Ngang
- 1. Giới Thiệu Về Chuyển Động Ném Ngang
- 2. Các Thành Phần Của Chuyển Động Ném Ngang
- 3. Các Công Thức Quan Trọng
- 4. Ví Dụ Thực Tế Và Bài Tập Áp Dụng
- 5. Ứng Dụng Của Lý Thuyết Chuyển Động Ném Ngang
- 6. Những Sai Lầm Thường Gặp và Cách Khắc Phục
- 7. Tài Liệu Tham Khảo và Nguồn Học Tập
Lý Thuyết Chuyển Động Ném Ngang
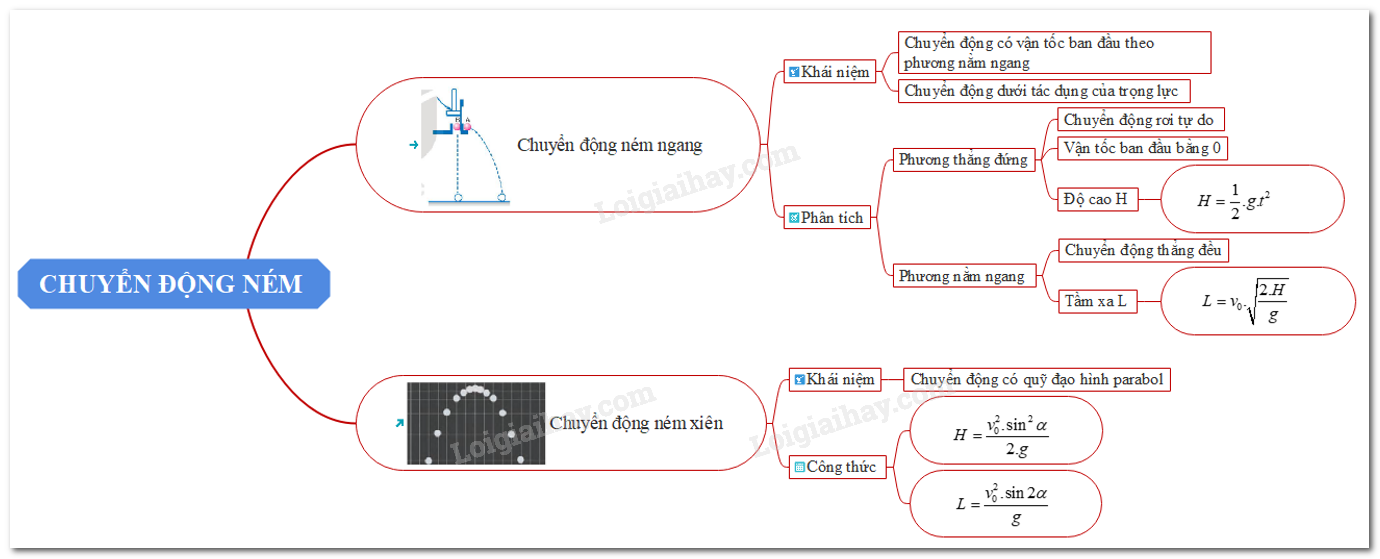
Lý thuyết chuyển động ném ngang là một phần quan trọng của cơ học cổ điển, mô tả chuyển động của vật thể khi nó bị ném với vận tốc ban đầu ngang so với mặt đất. Dưới đây là tổng hợp chi tiết về lý thuyết này.
1. Khái Niệm Cơ Bản
Chuyển động ném ngang là sự kết hợp của hai chuyển động độc lập: chuyển động ngang với vận tốc không đổi và chuyển động rơi tự do theo phương thẳng đứng dưới tác dụng của trọng lực.
2. Các Thành Phần Chính
- Vận tốc Ngang (vx): Là vận tốc không đổi của vật thể theo phương ngang.
- Thời Gian (t): Thời gian từ khi vật thể được ném đến khi nó chạm đất.
- Chiều Cao (h): Khoảng cách từ điểm ném đến mặt đất.
- Quỹ Đạo (x): Đường đi của vật thể trong không gian.
3. Công Thức Quan Trọng
Các công thức cơ bản để tính toán chuyển động ném ngang là:
- Khoảng cách ngang: \( x = v_x \cdot t \)
- Thời gian rơi: \( t = \sqrt{\frac{2h}{g}} \)
- Khoảng cách ngang: \( x = v_x \cdot \sqrt{\frac{2h}{g}} \)
4. Ví Dụ Thực Tế
Ví dụ, khi một viên đá được ném ngang từ một vách đá với vận tốc 10 m/s, và chiều cao của vách đá là 20 m. Thời gian viên đá rơi xuống có thể được tính bằng cách sử dụng công thức trên, và từ đó ta có thể tính được khoảng cách ngang mà viên đá đã di chuyển trước khi chạm đất.
5. Ứng Dụng Thực Tiễn
Lý thuyết chuyển động ném ngang được áp dụng trong nhiều lĩnh vực như thể thao (bóng ném, bắn cung), kỹ thuật (tính toán đường bay của tên lửa), và trong cuộc sống hàng ngày để hiểu các hiện tượng vật lý.
| Thông Số | Giá Trị |
|---|---|
| Vận tốc Ngang (vx) | 10 m/s |
| Chiều Cao (h) | 20 m |
| Thời Gian (t) | \(\sqrt{\frac{2 \times 20}{9.8}} \approx 2.02 \text{ s}\) |
| Khoảng Cách Ngang (x) | 10 m/s × 2.02 s = 20.2 m |
.png)
1. Giới Thiệu Về Chuyển Động Ném Ngang
Chuyển động ném ngang là một phần quan trọng trong cơ học cổ điển, mô tả hành vi của vật thể khi nó được ném với vận tốc ngang và chỉ chịu tác dụng của trọng lực trong chiều dọc. Đây là một chủ đề cơ bản giúp chúng ta hiểu rõ hơn về sự kết hợp của các lực và chuyển động trong không gian.
1.1. Khái Niệm Cơ Bản
Chuyển động ném ngang là sự kết hợp của hai chuyển động độc lập:
- Chuyển động ngang: Vật thể chuyển động với vận tốc không đổi theo phương ngang.
- Chuyển động thẳng đứng: Vật thể rơi tự do dưới tác dụng của trọng lực.
1.2. Đặc Điểm và Nguyên Tắc
Khi vật thể được ném ngang, nó sẽ di chuyển theo một quỹ đạo parabol. Đặc điểm chính của chuyển động ném ngang bao gồm:
- Vận tốc ngang (vx): Là vận tốc không đổi và không bị ảnh hưởng bởi trọng lực.
- Thời gian rơi (t): Thời gian từ khi vật thể được ném đến khi nó chạm đất, phụ thuộc vào chiều cao của điểm ném.
- Quỹ đạo: Đường đi của vật thể có dạng parabol, được xác định bởi vận tốc ngang và thời gian rơi.
1.3. Công Thức Tính Toán
Để tính toán chuyển động ném ngang, các công thức cơ bản là:
| Thành Phần | Công Thức |
|---|---|
| Khoảng cách ngang (x) | \[ x = v_x \cdot t \] |
| Thời gian rơi (t) | \[ t = \sqrt{\frac{2h}{g}} \] |
| Khoảng cách ngang từ thời gian rơi | \[ x = v_x \cdot \sqrt{\frac{2h}{g}} \] |
Trong đó:
- vx: Vận tốc ngang
- h: Chiều cao điểm ném
- g: Gia tốc trọng trường (khoảng 9.8 m/s²)
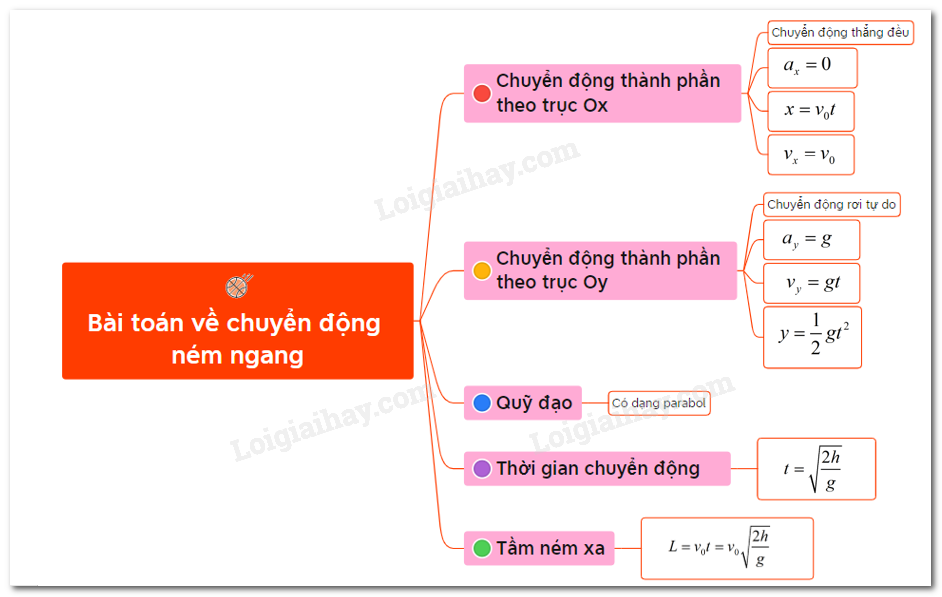
2. Các Thành Phần Của Chuyển Động Ném Ngang
Chuyển động ném ngang bao gồm nhiều thành phần quan trọng, mỗi thành phần đóng vai trò khác nhau trong việc mô tả và phân tích chuyển động của vật thể. Dưới đây là các thành phần cơ bản của chuyển động ném ngang:
2.1. Vận Tốc Ngang (vx)
Vận tốc ngang là thành phần quan trọng của chuyển động ném ngang. Đây là vận tốc mà vật thể có khi được ném, và nó không thay đổi trong suốt quá trình chuyển động vì không có lực tác động ngang:
- Đặc điểm: Không thay đổi theo thời gian.
- Đơn vị: Mét trên giây (m/s).
2.2. Thời Gian Rơi (t)
Thời gian rơi là khoảng thời gian mà vật thể cần để từ lúc ném đến khi chạm đất. Thời gian này phụ thuộc vào chiều cao của điểm ném:
- Công thức: \[ t = \sqrt{\frac{2h}{g}} \]
- Chiều cao: Chiều cao từ điểm ném đến mặt đất.
- Gia tốc trọng trường (g): Khoảng 9.8 m/s².
2.3. Chiều Cao (h)
Chiều cao là khoảng cách từ điểm ném đến mặt đất. Đây là yếu tố quan trọng quyết định thời gian rơi của vật thể:
- Ảnh hưởng: Chiều cao càng lớn, thời gian rơi càng dài.
- Đơn vị: Mét (m).
2.4. Quỹ Đạo
Quỹ đạo của vật thể trong chuyển động ném ngang có dạng parabol. Đây là kết quả của sự kết hợp giữa chuyển động ngang và chuyển động rơi tự do:
- Đặc điểm: Đường cong parabol.
- Yếu tố ảnh hưởng: Vận tốc ngang và thời gian rơi.
2.5. Công Thức Tính Toán Các Thành Phần
| Thành Phần | Công Thức |
|---|---|
| Khoảng cách ngang (x) | \[ x = v_x \cdot t \] |
| Thời gian rơi (t) | \[ t = \sqrt{\frac{2h}{g}} \] |
| Khoảng cách ngang từ chiều cao (h) | \[ x = v_x \cdot \sqrt{\frac{2h}{g}} \] |

3. Các Công Thức Quan Trọng
Trong lý thuyết chuyển động ném ngang, các công thức toán học đóng vai trò quan trọng trong việc mô tả và tính toán các đặc điểm của chuyển động. Dưới đây là các công thức cơ bản cần biết:
3.1. Công Thức Tính Khoảng Cách Ngang (x)
Khoảng cách ngang là khoảng cách mà vật thể di chuyển theo phương ngang trong suốt thời gian rơi:
Công thức:
- \[ x = v_x \cdot t \]
Trong đó:
- vx: Vận tốc ngang của vật thể.
- t: Thời gian rơi từ điểm ném đến khi vật thể chạm đất.
3.2. Công Thức Tính Thời Gian Rơi (t)
Thời gian rơi là khoảng thời gian mà vật thể cần để từ khi được ném cho đến khi chạm đất:
Công thức:
- \[ t = \sqrt{\frac{2h}{g}} \]
Trong đó:
- h: Chiều cao từ điểm ném đến mặt đất.
- g: Gia tốc trọng trường (khoảng 9.8 m/s²).
3.3. Công Thức Tính Khoảng Cách Ngang Theo Chiều Cao (h)
Công thức này giúp tính toán khoảng cách ngang dựa trên chiều cao của điểm ném và vận tốc ngang:
Công thức:
- \[ x = v_x \cdot \sqrt{\frac{2h}{g}} \]
3.4. Ví Dụ Minh Họa
Giả sử vật thể được ném với vận tốc ngang 15 m/s từ độ cao 20 m. Áp dụng các công thức trên, ta có:
- Tính thời gian rơi: \[ t = \sqrt{\frac{2 \times 20}{9.8}} \approx 2.02 \text{ giây} \]
- Tính khoảng cách ngang: \[ x = 15 \cdot 2.02 \approx 30.3 \text{ mét} \]
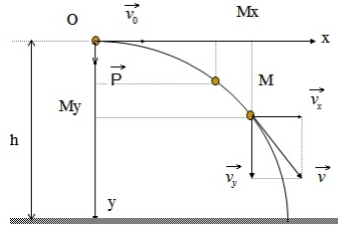
4. Ví Dụ Thực Tế Và Bài Tập Áp Dụng
Để hiểu rõ hơn về lý thuyết chuyển động ném ngang, chúng ta có thể áp dụng các công thức đã học vào những ví dụ thực tế và bài tập. Dưới đây là một số ví dụ và bài tập giúp bạn nắm vững kiến thức:
4.1. Ví Dụ Thực Tế
Ví dụ 1: Ném một viên đá từ mép của một vách đá cao 50 mét với vận tốc ngang 20 m/s. Hãy tính toán:
- Thời gian viên đá rơi xuống đất.
- Khoảng cách ngang mà viên đá di chuyển được trước khi chạm đất.
Giải pháp:
- Thời gian rơi: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 50}{9.8}} \approx 3.19 \text{ giây} \]
- Khoảng cách ngang: \[ x = v_x \cdot t = 20 \cdot 3.19 \approx 63.8 \text{ mét} \]
Ví dụ 2: Một quả bóng được ném với vận tốc ngang 15 m/s từ độ cao 30 mét. Tính:
- Thời gian quả bóng rơi xuống đất.
- Khoảng cách ngang mà quả bóng di chuyển trước khi chạm đất.
Giải pháp:
- Thời gian rơi: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 30}{9.8}} \approx 2.47 \text{ giây} \]
- Khoảng cách ngang: \[ x = v_x \cdot t = 15 \cdot 2.47 \approx 37.05 \text{ mét} \]
4.2. Bài Tập Áp Dụng
Bài tập 1: Một viên bi được ném từ độ cao 40 mét với vận tốc ngang 25 m/s. Xác định:
- Thời gian viên bi rơi xuống đất.
- Khoảng cách ngang mà viên bi di chuyển được trước khi chạm đất.
Giải pháp:
- Thời gian rơi: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 40}{9.8}} \approx 2.86 \text{ giây} \]
- Khoảng cách ngang: \[ x = v_x \cdot t = 25 \cdot 2.86 \approx 71.5 \text{ mét} \]
Bài tập 2: Một viên đá được ném với vận tốc ngang 10 m/s từ độ cao 10 mét. Tính:
- Thời gian viên đá rơi xuống đất.
- Khoảng cách ngang mà viên đá di chuyển được trước khi chạm đất.
Giải pháp:
- Thời gian rơi: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 10}{9.8}} \approx 1.43 \text{ giây} \]
- Khoảng cách ngang: \[ x = v_x \cdot t = 10 \cdot 1.43 \approx 14.3 \text{ mét} \]

5. Ứng Dụng Của Lý Thuyết Chuyển Động Ném Ngang
Lý thuyết chuyển động ném ngang không chỉ là một phần quan trọng trong cơ học mà còn có nhiều ứng dụng thực tiễn trong đời sống và các lĩnh vực khác. Dưới đây là một số ứng dụng nổi bật:
5.1. Ứng Dụng Trong Thể Thao
Chuyển động ném ngang được áp dụng trong nhiều môn thể thao như bóng rổ, bóng đá, và golf. Ví dụ:
- Bóng Rổ: Các vận động viên cần tính toán góc ném và vận tốc để bóng rổ có thể vào rổ một cách chính xác.
- Bóng Đá: Trong các cú đá xa, cầu thủ cần hiểu rõ về chuyển động ném ngang để điều chỉnh lực và góc đá sao cho bóng đi đúng hướng và đạt được khoảng cách mong muốn.
- Golf: Golfer cần tính toán đường bay của quả bóng để đạt được mục tiêu trên sân golf, bao gồm điều chỉnh vận tốc và góc của cú đánh.
5.2. Ứng Dụng Trong Kỹ Thuật
Các kỹ sư và nhà thiết kế sử dụng lý thuyết chuyển động ném ngang trong nhiều lĩnh vực kỹ thuật để thiết kế và phân tích các hệ thống:
- Thiết Kế Tên Lửa: Trong ngành hàng không vũ trụ, lý thuyết này giúp dự đoán và tối ưu hóa đường bay của tên lửa và vệ tinh.
- Thiết Kế Cầu và Tòa Nhà: Kỹ sư sử dụng các nguyên lý của chuyển động ném ngang để tính toán các tải trọng và phân tích sự ổn định của các cấu trúc xây dựng.
5.3. Ứng Dụng Trong Giải Trí
Trong ngành giải trí và trò chơi điện tử, lý thuyết chuyển động ném ngang được áp dụng để tạo ra các hiệu ứng vật lý chân thực:
- Trò Chơi Điện Tử: Các nhà phát triển trò chơi sử dụng lý thuyết này để mô phỏng chuyển động của các vật thể trong trò chơi, tạo ra trải nghiệm chân thực cho người chơi.
- Hiệu Ứng Đặc Biệt Trong Phim: Trong sản xuất phim và truyền hình, lý thuyết chuyển động ném ngang được sử dụng để thiết kế các cảnh quay hành động, đặc biệt là các cảnh ném hoặc rơi.
5.4. Ứng Dụng Trong Giáo Dục
Lý thuyết chuyển động ném ngang là một phần quan trọng trong giáo dục vật lý, giúp học sinh và sinh viên hiểu rõ hơn về các nguyên lý cơ bản của chuyển động và lực:
- Giảng Dạy: Các bài học và thí nghiệm về chuyển động ném ngang giúp sinh viên nắm vững kiến thức cơ bản về chuyển động và lực trong vật lý.
- Thí Nghiệm Trong Phòng Thí Nghiệm: Thực hiện các thí nghiệm liên quan đến chuyển động ném ngang giúp sinh viên áp dụng lý thuyết vào thực tiễn và phát triển kỹ năng phân tích và giải quyết vấn đề.
XEM THÊM:
6. Những Sai Lầm Thường Gặp và Cách Khắc Phục
Trong quá trình nghiên cứu và ứng dụng lý thuyết chuyển động ném ngang, một số sai lầm phổ biến có thể xảy ra. Dưới đây là những sai lầm thường gặp và cách khắc phục chúng:
6.1. Những Sai Lầm Trong Tính Toán
- Nhầm lẫn về các thành phần của vận tốc: Trong chuyển động ném ngang, cần phân biệt rõ giữa vận tốc ngang và vận tốc dọc. Đảm bảo rằng bạn đang sử dụng đúng thành phần vận tốc trong các công thức tính toán.
- Không tính đến lực cản không khí: Trong các bài toán lý thuyết, thường không tính đến lực cản không khí. Tuy nhiên, trong thực tế, lực cản này có thể ảnh hưởng đến quỹ đạo của vật thể. Hãy nhớ rằng điều này có thể làm thay đổi kết quả tính toán trong các tình huống cụ thể.
- Nhầm lẫn đơn vị: Đảm bảo rằng tất cả các đơn vị được sử dụng trong các phép tính là đồng nhất, chẳng hạn như mét và giây. Việc chuyển đổi không chính xác giữa các đơn vị có thể dẫn đến sai số lớn trong kết quả.
6.2. Cách Điều Chỉnh và Cải Thiện
- Kiểm tra kỹ lưỡng các thành phần của vận tốc: Đảm bảo rằng bạn đã phân tách và áp dụng đúng các thành phần của vận tốc khi tính toán. Sử dụng phương pháp phân tích vector để giúp làm rõ vấn đề.
- Thực hiện các thí nghiệm thực tế: Để kiểm tra và điều chỉnh lý thuyết, thực hiện các thí nghiệm thực tế có thể giúp bạn hiểu rõ hơn về ảnh hưởng của lực cản không khí và các yếu tố khác.
- Đảm bảo sự chính xác trong các phép đo và chuyển đổi đơn vị: Sử dụng các công cụ và phần mềm hỗ trợ để đảm bảo rằng tất cả các phép đo và chuyển đổi đơn vị là chính xác. Sử dụng máy tính và bảng chuyển đổi đơn vị có thể giúp tránh sai sót.
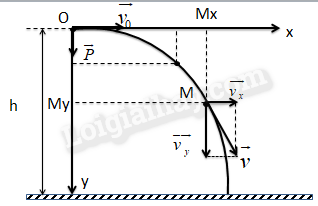
7. Tài Liệu Tham Khảo và Nguồn Học Tập
Để tìm hiểu sâu hơn về lý thuyết chuyển động ném ngang và áp dụng kiến thức vào thực tế, bạn có thể tham khảo các tài liệu sau:
7.1. Sách và Tài Liệu Đọc Thêm
- “Cơ Học Đại Cương” của H. D. Young và R. A. Freedman: Đây là một cuốn sách cơ bản và đầy đủ về cơ học, cung cấp nền tảng vững chắc về lý thuyết chuyển động ném ngang.
- “Cơ Học Kỹ Thuật” của Trịnh Văn Hùng: Cuốn sách này cung cấp các ví dụ thực tế và bài tập áp dụng, giúp người đọc hiểu rõ hơn về các công thức và ứng dụng của chuyển động ném ngang.
- “Lý Thuyết và Bài Tập Cơ Học” của Nguyễn Văn Hùng: Sách này cung cấp lý thuyết chi tiết và nhiều bài tập thực hành, rất hữu ích cho việc ôn luyện và áp dụng kiến thức về chuyển động ném ngang.
7.2. Tài Liệu Trực Tuyến và Khóa Học
- Coursera - “Introduction to Mechanics”: Khóa học này cung cấp cái nhìn tổng quan về cơ học, bao gồm các chủ đề liên quan đến chuyển động ném ngang.
- Khan Academy - “Physics: Kinematics”: Khan Academy cung cấp các bài giảng miễn phí về cơ học, với các video và bài tập liên quan đến chuyển động ném ngang.
- edX - “Fundamentals of Physics”: Khóa học từ edX giúp bạn hiểu rõ hơn về các nguyên lý cơ bản trong vật lý, bao gồm chuyển động ném ngang.