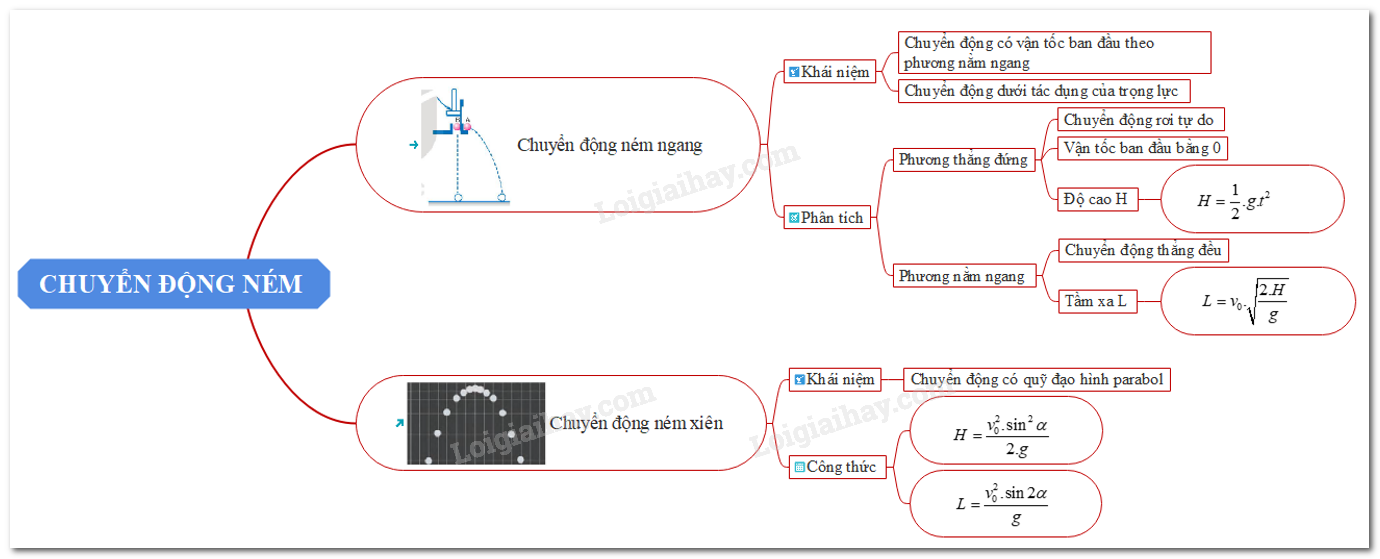
Chủ đề chuyển động ném ngang là chuyển động: Chuyển động ném ngang là một khái niệm thú vị trong vật lý, mô tả cách một vật thể chuyển động khi được ném với một vận tốc ban đầu theo phương ngang. Trong bài viết này, chúng ta sẽ cùng khám phá chi tiết về lý thuyết chuyển động ném ngang, các phương trình cơ bản, và ứng dụng thực tiễn của nó trong đời sống và khoa học. Hãy theo dõi để hiểu rõ hơn về chủ đề này!
Mục lục
- Thông tin về "Chuyển động ném ngang là chuyển động"
- 1. Giới thiệu về chuyển động ném ngang
- 2. Các phương trình và tính toán trong chuyển động ném ngang
- 3. Ứng dụng của chuyển động ném ngang trong thực tiễn
- 4. Ví dụ cụ thể và bài tập thực hành
- 5. Các vấn đề thường gặp và cách khắc phục
- 6. Kết luận và tổng kết
Thông tin về "Chuyển động ném ngang là chuyển động"
Chuyển động ném ngang là một chủ đề thú vị trong lĩnh vực vật lý. Dưới đây là tổng hợp thông tin chi tiết về chủ đề này từ kết quả tìm kiếm trên Bing tại Việt Nam:
Khái niệm cơ bản
Chuyển động ném ngang là một loại chuyển động trong vật lý mà trong đó một vật thể được ném với một vận tốc ban đầu theo phương ngang, đồng thời chịu tác động của trọng lực. Đặc điểm chính của chuyển động ném ngang bao gồm:
- Vận tốc ban đầu theo phương ngang là không đổi.
- Chuyển động theo phương đứng là do trọng lực tác động và được mô tả bằng chuyển động rơi tự do.
Đặc điểm và ứng dụng
Chuyển động ném ngang có thể được mô tả bằng các phương trình vật lý đơn giản. Các phương trình chính bao gồm:
- Vận tốc theo phương ngang: \( v_x = v_0 \)
- Thời gian rơi: \( t = \sqrt{\frac{2h}{g}} \)
- Khoảng cách ném ngang: \( d = v_x \cdot t \)
Ứng dụng thực tế
Chuyển động ném ngang được ứng dụng rộng rãi trong nhiều lĩnh vực:
- Trong thể thao, ví dụ như bóng đá hoặc bóng rổ, nơi mà các cầu thủ cần tính toán các yếu tố chuyển động của bóng.
- Trong kỹ thuật và công nghệ, ví dụ như thiết kế đường đạn hoặc các thiết bị phóng vật thể.
Ví dụ cụ thể
Ví dụ đơn giản về chuyển động ném ngang có thể là việc ném một viên đá từ một đỉnh cao. Viên đá sẽ di chuyển theo phương ngang với vận tốc ném ban đầu, đồng thời rơi xuống dưới tác động của trọng lực. Các yếu tố như chiều cao của đỉnh và vận tốc ném sẽ ảnh hưởng đến khoảng cách mà viên đá đạt được.
Kết luận
Chuyển động ném ngang là một khái niệm quan trọng trong vật lý với nhiều ứng dụng thực tiễn. Hiểu rõ các yếu tố và phương trình liên quan giúp chúng ta áp dụng vào nhiều tình huống khác nhau trong đời sống và nghiên cứu khoa học.

.png)
1. Giới thiệu về chuyển động ném ngang
Chuyển động ném ngang là một loại chuyển động cơ bản trong vật lý, đặc biệt là trong cơ học. Đây là dạng chuyển động của một vật thể khi nó được ném theo hướng ngang với mặt đất và chịu tác động của trọng lực.
Chuyển động ném ngang có những đặc điểm chính sau:
- Khái niệm: Chuyển động ném ngang xảy ra khi một vật thể được ném với một vận tốc ngang ban đầu và chịu tác động của lực trọng trường. Vật thể không có lực tác động theo phương dọc (trừ trọng lực) và di chuyển theo một quỹ đạo parabol.
- Đặc điểm: Vận tốc ngang của vật thể không thay đổi do không có lực ma sát hay lực cản trong môi trường lý tưởng. Tuy nhiên, vật thể sẽ bị ảnh hưởng bởi trọng lực, gây ra chuyển động theo phương thẳng đứng xuống dưới.
Nguyên lý hoạt động của chuyển động ném ngang có thể được mô tả bằng các công thức toán học cơ bản. Cụ thể, chuyển động này có thể được phân tích thành hai thành phần độc lập: chuyển động ngang và chuyển động dọc.
Các công thức cơ bản áp dụng cho chuyển động ném ngang là:
- Vận tốc ngang: \( v_x = v_{0x} \), trong đó \( v_{0x} \) là vận tốc ngang ban đầu.
- Thời gian rơi: \( t = \sqrt{\frac{2h}{g}} \), trong đó \( h \) là độ cao từ đó vật thể được ném và \( g \) là gia tốc trọng trường.
- Khoảng cách ngang: \( x = v_x \cdot t \).
Như vậy, chuyển động ném ngang không chỉ đơn thuần là một khái niệm lý thuyết mà còn có ứng dụng thực tiễn quan trọng trong nhiều lĩnh vực khác nhau như thể thao, kỹ thuật và công nghệ.
2. Các phương trình và tính toán trong chuyển động ném ngang
Trong chuyển động ném ngang, việc tính toán và sử dụng các phương trình là rất quan trọng để xác định các đặc tính của chuyển động như khoảng cách, thời gian và vận tốc. Dưới đây là các phương trình cơ bản và cách tính toán liên quan đến chuyển động ném ngang.
2.1. Phương trình vận tốc và gia tốc
Trong chuyển động ném ngang, có hai thành phần vận tốc cần được xem xét: vận tốc ngang và vận tốc dọc.
- Vận tốc ngang: Vận tốc ngang của vật thể trong chuyển động ném ngang không thay đổi và được tính bằng công thức: \[ v_x = v_{0x} \] trong đó \( v_{0x} \) là vận tốc ngang ban đầu.
- Vận tốc dọc: Vận tốc dọc thay đổi theo thời gian do tác động của trọng lực. Công thức tính vận tốc dọc tại thời điểm \( t \) là: \[ v_y = v_{0y} - g \cdot t \] trong đó \( v_{0y} \) là vận tốc dọc ban đầu (thường bằng 0 trong trường hợp ném ngang), \( g \) là gia tốc trọng trường (khoảng 9.81 m/s²), và \( t \) là thời gian.
2.2. Tính toán khoảng cách và thời gian
Khoảng cách và thời gian trong chuyển động ném ngang có thể được tính toán bằng các công thức sau:
- Thời gian rơi: Thời gian mà vật thể cần để chạm đất phụ thuộc vào độ cao từ đó nó được ném. Công thức tính thời gian rơi \( t \) là: \[ t = \sqrt{\frac{2h}{g}} \] trong đó \( h \) là độ cao và \( g \) là gia tốc trọng trường.
- Khoảng cách ngang: Khoảng cách ngang mà vật thể di chuyển được trong thời gian \( t \) có thể tính bằng công thức: \[ x = v_x \cdot t \] trong đó \( v_x \) là vận tốc ngang và \( t \) là thời gian.
Như vậy, việc sử dụng các phương trình này giúp chúng ta phân tích và dự đoán hành trình của vật thể trong chuyển động ném ngang một cách chính xác và hiệu quả.

3. Ứng dụng của chuyển động ném ngang trong thực tiễn
Chuyển động ném ngang không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tiễn quan trọng trong đời sống hàng ngày và các lĩnh vực khác. Dưới đây là một số ứng dụng nổi bật của chuyển động ném ngang:
3.1. Trong thể thao
Chuyển động ném ngang có vai trò quan trọng trong nhiều môn thể thao, đặc biệt là những môn liên quan đến việc ném hoặc phóng vật thể.
- Bóng rổ: Khi cầu thủ ném bóng vào rổ, chuyển động của quả bóng có thể được mô tả bằng chuyển động ném ngang. Việc hiểu rõ về quỹ đạo và khoảng cách giúp cầu thủ ném bóng chính xác hơn.
- Bóng chày: Trong môn bóng chày, khi cầu thủ ném bóng về phía gôn, quỹ đạo của bóng thường là một đường cong parabol, tương tự như chuyển động ném ngang. Các vận động viên cần tính toán chính xác để đánh trúng bóng và đạt điểm số.
- Golf: Khi người chơi golf đánh bóng, quỹ đạo của bóng khi rời khỏi gậy cũng có thể được phân tích bằng chuyển động ném ngang, giúp cải thiện kỹ thuật và chính xác hơn trong các cú đánh.
3.2. Trong công nghệ và kỹ thuật
Chuyển động ném ngang cũng có ứng dụng rộng rãi trong các lĩnh vực công nghệ và kỹ thuật:
- Kỹ thuật hàng không: Trong thiết kế và phân tích các chuyến bay của tên lửa hoặc máy bay, các nhà kỹ thuật sử dụng các phương trình của chuyển động ném ngang để dự đoán quỹ đạo và tính toán các yếu tố như tốc độ và khoảng cách bay.
- Hệ thống điều khiển tự động: Trong các hệ thống điều khiển tự động như robot hoặc máy móc, việc tính toán chuyển động của các bộ phận hoặc sản phẩm có thể dựa trên các nguyên lý của chuyển động ném ngang để đảm bảo độ chính xác và hiệu quả.
- Thiết kế và xây dựng: Trong các ứng dụng xây dựng, như tính toán các quỹ đạo của các vật thể được ném từ một cấu trúc cao, các kỹ sư sử dụng chuyển động ném ngang để đảm bảo sự an toàn và chính xác của các thiết kế.
Nhờ vào các ứng dụng đa dạng này, chuyển động ném ngang không chỉ là một khái niệm lý thuyết mà còn đóng góp tích cực vào nhiều lĩnh vực khác nhau trong cuộc sống và công việc hàng ngày.

4. Ví dụ cụ thể và bài tập thực hành
Để hiểu rõ hơn về chuyển động ném ngang, việc áp dụng lý thuyết vào các ví dụ cụ thể và bài tập thực hành là rất quan trọng. Dưới đây là một số ví dụ và bài tập giúp bạn làm quen với khái niệm này.
4.1. Ví dụ về ném đá từ độ cao
Giả sử bạn ném một viên đá từ một độ cao \( h \) trên mặt đất với vận tốc ngang \( v_x \). Để tính toán quỹ đạo của viên đá, bạn có thể áp dụng các công thức sau:
- Thời gian rơi: Thời gian mà viên đá cần để chạm đất được tính bằng công thức: \[ t = \sqrt{\frac{2h}{g}} \] trong đó \( h \) là độ cao và \( g \) là gia tốc trọng trường (khoảng 9.81 m/s²).
- Khoảng cách ngang: Khoảng cách ngang mà viên đá di chuyển được trong thời gian \( t \) là: \[ x = v_x \cdot t \] trong đó \( v_x \) là vận tốc ngang.
Ví dụ, nếu viên đá được ném từ độ cao 20 m với vận tốc ngang 15 m/s, bạn có thể tính toán thời gian rơi và khoảng cách ngang như sau:
- Thời gian rơi: \[ t = \sqrt{\frac{2 \times 20}{9.81}} \approx 2.02 \text{ giây} \]
- Khoảng cách ngang: \[ x = 15 \times 2.02 \approx 30.3 \text{ mét} \]
4.2. Bài tập áp dụng và giải pháp
Hãy giải bài tập sau để áp dụng kiến thức về chuyển động ném ngang:
- Bài tập: Một viên đạn được bắn ra từ một pháo với vận tốc ngang 25 m/s từ một độ cao 45 m so với mặt đất. Tính khoảng cách ngang mà viên đạn di chuyển trước khi chạm đất.
- Giải pháp:
- Tính thời gian rơi: \[ t = \sqrt{\frac{2 \times 45}{9.81}} \approx 3.03 \text{ giây} \]
- Tính khoảng cách ngang: \[ x = 25 \times 3.03 \approx 75.75 \text{ mét} \]
Qua các ví dụ và bài tập thực hành, bạn có thể áp dụng lý thuyết về chuyển động ném ngang vào các tình huống thực tế để tính toán quỹ đạo và khoảng cách của các vật thể. Điều này giúp cải thiện sự hiểu biết và kỹ năng giải quyết vấn đề trong các tình huống thực tế.

5. Các vấn đề thường gặp và cách khắc phục
Khi làm việc với chuyển động ném ngang, có một số vấn đề phổ biến mà bạn có thể gặp phải. Dưới đây là các vấn đề thường gặp và cách khắc phục chúng để đảm bảo tính chính xác trong tính toán và ứng dụng.
5.1. Các lỗi phổ biến trong tính toán
- Lỗi do không tính đến lực cản: Trong các bài toán lý thuyết, chúng ta thường bỏ qua lực cản của không khí. Tuy nhiên, trong thực tế, lực cản này có thể làm giảm tốc độ của vật thể. Để khắc phục, hãy đảm bảo rằng các bài toán thực tế đã tính đến các yếu tố lực cản, hoặc thử nghiệm để xác định ảnh hưởng của nó.
- Không chính xác trong việc xác định vận tốc ngang: Vận tốc ngang có thể thay đổi do các yếu tố như ma sát hoặc lỗi trong đo đạc. Để khắc phục, hãy sử dụng thiết bị đo chính xác và thực hiện nhiều phép đo để đảm bảo độ tin cậy.
- Áp dụng sai công thức: Đôi khi, việc áp dụng công thức tính toán không chính xác có thể dẫn đến kết quả sai. Hãy kiểm tra lại các công thức và bước tính toán để đảm bảo rằng bạn đang sử dụng đúng công thức cho từng trường hợp cụ thể.
5.2. Cách kiểm tra và điều chỉnh kết quả
- Kiểm tra kết quả bằng cách thực nghiệm: Một cách hiệu quả để kiểm tra các tính toán là thực hiện các thí nghiệm thực tế. So sánh kết quả thực nghiệm với kết quả lý thuyết để xác định tính chính xác và điều chỉnh nếu cần.
- So sánh với các ví dụ đã biết: Sử dụng các bài tập và ví dụ đã biết để so sánh và kiểm tra các tính toán của bạn. Điều này giúp xác nhận tính chính xác của kết quả và phát hiện bất kỳ sai sót nào.
- Thực hiện các bước kiểm tra kỹ lưỡng: Đảm bảo rằng bạn đã thực hiện đầy đủ các bước kiểm tra và phân tích cần thiết trước khi kết luận. Điều này bao gồm việc kiểm tra các giá trị đầu vào, công thức sử dụng và kết quả cuối cùng.
Việc nhận diện và khắc phục các vấn đề thường gặp trong chuyển động ném ngang giúp cải thiện độ chính xác và hiệu quả của các tính toán và ứng dụng. Hãy áp dụng các phương pháp kiểm tra và điều chỉnh để đảm bảo rằng bạn có được kết quả đáng tin cậy và chính xác.
XEM THÊM:
6. Kết luận và tổng kết
Chuyển động ném ngang là một khái niệm cơ bản trong vật lý, có ứng dụng rộng rãi và quan trọng trong nhiều lĩnh vực. Việc hiểu và áp dụng các nguyên lý của chuyển động ném ngang không chỉ giúp giải quyết các bài toán lý thuyết mà còn hỗ trợ trong các ứng dụng thực tiễn.
Tầm quan trọng của chuyển động ném ngang: Chuyển động ném ngang giúp chúng ta phân tích và dự đoán hành trình của các vật thể khi chúng được ném hoặc phóng từ một độ cao nhất định. Điều này rất quan trọng trong các lĩnh vực như thể thao, kỹ thuật và khoa học. Việc nắm vững các phương trình và nguyên lý cơ bản của chuyển động ném ngang giúp chúng ta giải quyết các bài toán phức tạp và cải thiện kỹ năng phân tích.
Hướng phát triển và nghiên cứu tiếp theo: Các nghiên cứu về chuyển động ném ngang có thể được mở rộng để bao gồm các yếu tố như lực cản của không khí, các yếu tố môi trường, và các ứng dụng công nghệ tiên tiến. Việc áp dụng các mô hình toán học và thực nghiệm mới có thể giúp nâng cao độ chính xác và hiệu quả trong các lĩnh vực liên quan.
Nhìn chung, việc hiểu rõ và áp dụng chuyển động ném ngang không chỉ giúp giải quyết các vấn đề lý thuyết mà còn mang lại lợi ích thiết thực trong nhiều lĩnh vực khác nhau. Điều này nhấn mạnh tầm quan trọng của việc nghiên cứu và ứng dụng các nguyên lý vật lý cơ bản trong thực tế.