Chuyển động Ném Xiên: Tìm hiểu Toàn Diện và Ứng dụng Thực Tiễn

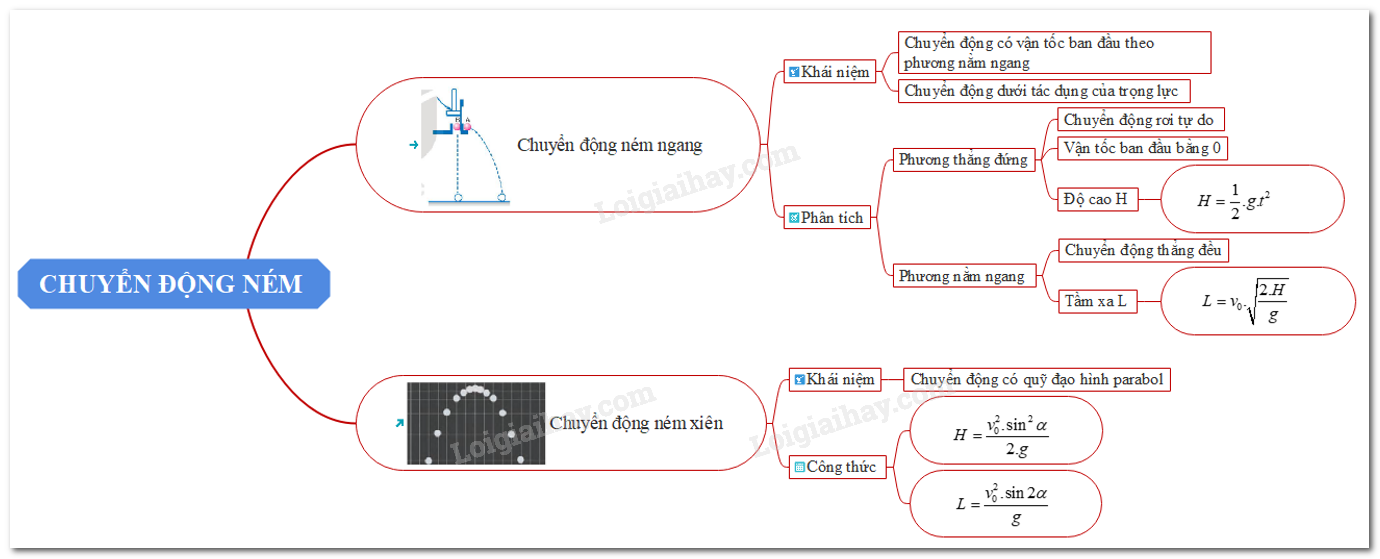
Chuyển động ném xiên là một chủ đề quan trọng trong vật lý học, thường được giảng dạy trong các trường trung học phổ thông và đại học. Nó bao gồm việc nghiên cứu quỹ đạo của một vật khi được ném lên không trung theo một góc xiên so với phương ngang. Đây là dạng chuyển động phổ biến trong nhiều tình huống thực tế như bóng đá, bóng rổ, và các hoạt động thể thao khác.

Các loại chuyển động ném

• Chuyển động ném ngang: Đây là trường hợp đặc biệt của chuyển động ném xiên, trong đó vật được ném theo phương ngang với góc ném \( \alpha = 0^\circ \).
• Chuyển động ném xiên: Trong trường hợp này, vật được ném với một góc \( \alpha \) bất kỳ ( \( 0^\circ < \alpha < 90^\circ \)) so với phương ngang.
• Chuyển động ném thẳng đứng: Khi vật được ném thẳng đứng lên trên với góc ném \( \alpha = 90^\circ \).

Phương trình chuyển động ném xiên

Phương trình quỹ đạo của một vật bị ném xiên được biểu diễn bằng:

\[
y = x \tan(\alpha) - \frac{g x^2}{2v_0^2 \cos^2(\alpha)}
\]

Trong đó:

• \( y \): độ cao của vật tại vị trí \( x \) (m).
• \( x \): khoảng cách ngang từ vị trí ném ban đầu (m).
• \( \alpha \): góc ném ban đầu so với phương ngang (độ).
• \( v_0 \): vận tốc ban đầu (m/s).
• \( g \): gia tốc trọng trường (khoảng 9.81 m/s²).

Ví dụ về bài tập chuyển động ném xiên

Xét một trường hợp cụ thể, một người ném một hòn đá với vận tốc ban đầu \( v_0 = 20 \, m/s \) và góc ném \( \alpha = 45^\circ \). Hãy tính tầm bay xa nhất \( L \) của hòn đá.

Để tìm tầm bay xa nhất, chúng ta sử dụng công thức:

\[
L = \frac{v_0^2 \sin(2\alpha)}{g}
\]

Thay giá trị vào:

\[
L = \frac{20^2 \times \sin(90^\circ)}{9.81} \approx 40.8 \, m
\]

Ứng dụng của chuyển động ném xiên

• Thể thao: Các môn thể thao như bóng đá, bóng rổ, và ném lao đều ứng dụng nguyên lý chuyển động ném xiên để đạt hiệu quả cao nhất.
• Kỹ thuật: Trong kỹ thuật quân sự, chuyển động ném xiên được sử dụng để tính toán tầm bắn của đạn pháo và tên lửa.
• Giáo dục: Đây là một trong những chủ đề cốt lõi trong giảng dạy vật lý tại các trường phổ thông và đại học.

Chuyển động ném xiên không chỉ là một lý thuyết quan trọng trong vật lý mà còn có nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày và các ngành kỹ thuật.

• 1. Khái niệm về Chuyển động Ném Xiên

  • 1.1. Định nghĩa và ý nghĩa của chuyển động ném xiên

  • 1.2. Các loại chuyển động ném và sự khác biệt

• 2. Các Phương Trình Cơ Bản

  • 2.1. Phương trình quỹ đạo của chuyển động ném xiên

  • 2.2. Công thức tính tầm bay xa, độ cao cực đại

  • 2.3. Các yếu tố ảnh hưởng đến quỹ đạo

• 3. Phân tích Lực Tác Động Trong Chuyển Động Ném Xiên

  • 3.1. Tác động của lực hấp dẫn

  • 3.2. Ảnh hưởng của lực cản không khí

  • 3.3. Sự tương tác giữa các lực

• 4. Ứng Dụng Thực Tế của Chuyển Động Ném Xiên

  • 4.1. Ứng dụng trong thể thao

  • 4.2. Ứng dụng trong kỹ thuật quân sự

  • 4.3. Ứng dụng trong các lĩnh vực khác

• 5. Bài Tập Thực Hành và Giải Thích Chi Tiết

  • 5.1. Bài tập cơ bản về chuyển động ném xiên

  • 5.2. Bài tập nâng cao và phân tích kết quả

  • 5.3. Các lỗi thường gặp khi giải bài tập

• 6. Nghiên Cứu Chuyên Sâu về Chuyển Động Ném Xiên

  • 6.1. Phân tích lý thuyết và thực nghiệm

  • 6.2. So sánh giữa mô hình lý tưởng và thực tế

  • 6.3. Ứng dụng nghiên cứu trong đời sống và kỹ thuật

Chuyển động ném xiên là một dạng chuyển động của vật thể trong không gian khi vật thể được ném lên với một góc so với phương ngang. Chuyển động này là sự kết hợp của hai chuyển động cơ bản: chuyển động thẳng đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng.

Trong chuyển động ném xiên, quỹ đạo của vật thể thường là một đường cong hình parabol, do ảnh hưởng của trọng lực. Công thức mô tả quỹ đạo này có thể được biểu diễn bằng các phương trình:

• Phương trình vị trí theo trục \(x\):

  \[ x = v_0 \cdot \cos(\theta) \cdot t \]

• Phương trình vị trí theo trục \(y\):

  \[ y = v_0 \cdot \sin(\theta) \cdot t - \frac{1}{2} g \cdot t^2 \]

Trong đó:

• \(v_0\) là vận tốc ban đầu của vật thể.
• \(\theta\) là góc ném so với phương ngang.
• \(g\) là gia tốc trọng trường (thường lấy giá trị \(9,81 \, m/s^2\)).
• \(t\) là thời gian kể từ khi vật bắt đầu chuyển động.

Nhờ vào các công thức này, chúng ta có thể dự đoán được vị trí của vật thể tại bất kỳ thời điểm nào trong quá trình chuyển động, đồng thời xác định được các đại lượng quan trọng như tầm bay xa, độ cao cực đại của vật thể.

Chuyển động ném là một hiện tượng vật lý phổ biến, trong đó một vật thể được ném hoặc bắn ra với một vận tốc ban đầu nhất định. Dựa trên đặc điểm và hướng chuyển động của vật thể, có thể phân loại chuyển động ném thành ba dạng chính:

• 2.1. Chuyển động ném ngang

  Chuyển động ném ngang xảy ra khi vật thể được ném theo phương ngang, tức là với góc ném \(\theta = 0^\circ\). Trong trường hợp này, vật thể chuyển động theo một đường thẳng ngang cho đến khi tác động của trọng lực khiến nó rơi xuống mặt đất. Quỹ đạo của chuyển động này là một phần của đường cong parabol.

• 2.2. Chuyển động ném xiên

  Chuyển động ném xiên là khi vật thể được ném lên với một góc \(\theta\) so với phương ngang, trong đó \(0^\circ < \theta < 90^\circ\). Đây là dạng chuyển động phức tạp hơn, kết hợp giữa chuyển động ngang và chuyển động rơi tự do theo chiều thẳng đứng. Quỹ đạo của vật thể trong chuyển động ném xiên cũng là một đường cong parabol.

• 2.3. Chuyển động ném thẳng đứng

  Chuyển động ném thẳng đứng xảy ra khi vật thể được ném hoặc bắn lên theo phương thẳng đứng, tức là với góc ném \(\theta = 90^\circ\). Trong trường hợp này, vật thể sẽ đi lên cho đến khi đạt tới độ cao cực đại, sau đó rơi trở lại do tác động của trọng lực. Quỹ đạo của chuyển động này là một đoạn thẳng theo chiều dọc.

Mỗi loại chuyển động ném có những đặc điểm và ứng dụng riêng trong thực tế. Hiểu rõ các loại chuyển động này giúp chúng ta dễ dàng áp dụng chúng vào các bài toán vật lý cũng như trong các lĩnh vực khác nhau của đời sống.

Chuyển động ném xiên là một dạng chuyển động parabol, trong đó vật thể được ném lên với một góc so với phương ngang và chịu tác động của trọng lực. Để mô tả quỹ đạo của chuyển động này, ta sử dụng các phương trình sau:

• 3.1. Phương trình quỹ đạo theo trục hoành (trục \(x\)):

  Vị trí của vật thể theo trục \(x\) tại thời điểm \(t\) được xác định bằng công thức:

  \[ x(t) = v_0 \cdot \cos(\theta) \cdot t \]

  Trong đó:

  • \(v_0\) là vận tốc ban đầu của vật thể.
  • \(\theta\) là góc ném so với phương ngang.
  • \(t\) là thời gian chuyển động.

• 3.2. Phương trình quỹ đạo theo trục tung (trục \(y\)):

  Vị trí của vật thể theo trục \(y\) tại thời điểm \(t\) được xác định bằng công thức:

  \[ y(t) = v_0 \cdot \sin(\theta) \cdot t - \frac{1}{2} \cdot g \cdot t^2 \]

  Trong đó:

  • \(g\) là gia tốc trọng trường, với giá trị xấp xỉ \(9,81 \, m/s^2\).

• 3.3. Phương trình quỹ đạo tổng quát:

  Bằng cách kết hợp hai phương trình trên, ta có thể tìm ra phương trình quỹ đạo tổng quát:

  \[ y(x) = x \cdot \tan(\theta) - \frac{g \cdot x^2}{2 \cdot v_0^2 \cdot \cos^2(\theta)} \]

  Phương trình này mô tả quỹ đạo parabol của vật thể trong mặt phẳng \(xy\), từ đó ta có thể xác định các đặc điểm quan trọng của chuyển động như độ cao cực đại và tầm xa của vật thể.

Phân tích quỹ đạo:

Phương trình quỹ đạo trên cho thấy rằng quỹ đạo của một vật thể ném xiên luôn là một đường cong parabol. Độ cao cực đại của quỹ đạo đạt được khi vận tốc theo phương \(y\) bằng không. Thời gian để đạt được độ cao cực đại là:

Và tầm xa của chuyển động, hay khoảng cách tối đa mà vật thể di chuyển theo trục \(x\), được tính bằng:

Hiểu rõ các phương trình và phân tích quỹ đạo giúp ta không chỉ giải quyết các bài toán vật lý mà còn áp dụng vào thực tế trong nhiều lĩnh vực khác nhau như kỹ thuật, thể thao và hàng không.

Quỹ đạo của một vật thể khi bị ném xiên chịu tác động bởi nhiều yếu tố khác nhau. Những yếu tố này ảnh hưởng trực tiếp đến hình dạng, độ cao, và tầm xa của quỹ đạo. Dưới đây là những yếu tố quan trọng nhất:

• 4.1. Góc ném (\(\theta\)):

  Góc ném là yếu tố quyết định đến quỹ đạo của vật thể. Khi góc ném \(\theta\) thay đổi, quỹ đạo sẽ thay đổi theo. Góc ném tối ưu để đạt được tầm xa lớn nhất trên một mặt phẳng nằm ngang là \(45^\circ\), khi không có sức cản không khí.

• 4.2. Vận tốc ban đầu (\(v_0\)):

  Vận tốc ban đầu là yếu tố then chốt ảnh hưởng đến cả độ cao cực đại và tầm xa của quỹ đạo. Vận tốc ban đầu càng lớn, vật thể càng đi xa và đạt được độ cao lớn hơn.

• 4.3. Gia tốc trọng trường (\(g\)):

  Gia tốc trọng trường là yếu tố không thể thay đổi, có giá trị khoảng \(9,81 \, m/s^2\) trên Trái Đất. Gia tốc này quyết định tốc độ rơi của vật thể và do đó ảnh hưởng đến hình dạng của quỹ đạo. Trên các hành tinh khác, giá trị \(g\) khác nhau sẽ làm quỹ đạo thay đổi đáng kể.

• 4.4. Kháng lực không khí:

  Trong thực tế, kháng lực không khí có ảnh hưởng lớn đến quỹ đạo của vật thể. Kháng lực làm giảm tốc độ của vật thể, làm cho quỹ đạo thực tế ngắn hơn và thấp hơn so với quỹ đạo lý thuyết trong chân không. Kháng lực phụ thuộc vào hình dạng, kích thước, và vận tốc của vật thể.

• 4.5. Độ cao xuất phát:

  Nếu vật thể được ném từ một độ cao so với mặt đất, quỹ đạo sẽ kéo dài hơn, và điểm rơi của vật thể sẽ xa hơn so với khi ném từ mặt đất.

Hiểu rõ các yếu tố này giúp chúng ta có thể dự đoán và điều chỉnh quỹ đạo trong các tình huống thực tế như thể thao, quân sự, hay các ngành công nghiệp kỹ thuật.

Chuyển động ném xiên là một hiện tượng phổ biến trong nhiều lĩnh vực, từ thể thao, quân sự đến các bài toán kỹ thuật và giảng dạy vật lý. Dưới đây là một số ứng dụng cụ thể của chuyển động ném xiên:

• 5.1. Trong thể thao

  Chuyển động ném xiên thường xuất hiện trong các môn thể thao như bóng rổ, bóng đá, và cầu lông. Ví dụ, khi một cầu thủ bóng rổ ném bóng vào rổ, quỹ đạo của quả bóng mô tả chuyển động ném xiên. Người chơi phải tính toán góc ném và lực tác dụng để tối ưu hóa quỹ đạo, đảm bảo bóng vào rổ với xác suất cao nhất.

• 5.2. Trong quân sự

  Trong quân sự, chuyển động ném xiên được ứng dụng trong việc phóng các loại vũ khí như đạn pháo, tên lửa và lựu đạn. Các yếu tố như góc ném, vận tốc ban đầu và trọng lực đều được cân nhắc kỹ lưỡng để đạt được tầm bắn tối đa và độ chính xác cao.

• 5.3. Trong các bài toán kỹ thuật

  Các kỹ sư và nhà khoa học thường sử dụng nguyên lý của chuyển động ném xiên để thiết kế các hệ thống phóng, máy móc và thiết bị. Chẳng hạn, khi thiết kế hệ thống phóng vệ tinh hoặc các vật thể vào quỹ đạo, việc tính toán quỹ đạo ném xiên là một phần quan trọng để đảm bảo vệ tinh đạt đến vị trí mong muốn.

• 5.4. Trong giảng dạy vật lý

  Chuyển động ném xiên là một chủ đề quan trọng trong giáo dục vật lý, giúp học sinh hiểu rõ hơn về các nguyên lý cơ bản của động lực học. Giáo viên thường sử dụng các thí nghiệm mô phỏng chuyển động ném xiên để minh họa cách các yếu tố như góc ném và vận tốc ban đầu ảnh hưởng đến quỹ đạo của vật thể.

Trong phần này, chúng ta sẽ đi vào chi tiết các bài tập liên quan đến chuyển động ném xiên và các phương pháp giải phổ biến. Các bài tập được phân chia thành ba cấp độ: cơ bản, nâng cao và phân tích lỗi thường gặp. Mỗi phần đều đi kèm với các hướng dẫn cụ thể và công thức cần thiết để giải quyết vấn đề.

6.1. Bài tập cơ bản

• Bài tập 1: Một vật được ném xiên từ mặt đất với vận tốc ban đầu \(v_0 = 20 \, \text{m/s}\) và góc ném \(\theta = 45^\circ\). Tính tầm xa của vật và thời gian bay.

  Giải: Sử dụng các công thức:

  • Tầm ném xa: \( R = \frac{v_0^2 \sin 2\theta}{g} \)
  • Thời gian bay: \( T = \frac{2v_0 \sin \theta}{g} \)

  Thay số vào công thức ta có:

  • Tầm xa: \( R = \frac{20^2 \sin 90^\circ}{10} = 40 \, \text{m} \)
  • Thời gian bay: \( T = \frac{2 \times 20 \times \sin 45^\circ}{10} \approx 2.83 \, \text{s} \)

• Bài tập 2: Một viên đạn được bắn theo phương xiên từ độ cao 100 m với vận tốc ban đầu \(v_0 = 50 \, \text{m/s}\) và góc ném \( \theta = 30^\circ \). Tính vận tốc của viên đạn khi chạm đất.

  Giải: Sử dụng phương trình vận tốc:

  • Vận tốc khi chạm đất: \( v = \sqrt{v_0^2 + (gt)^2} \)

  Thay số vào công thức ta có:

  • Vận tốc khi chạm đất: \( v \approx 54.77 \, \text{m/s} \)

6.2. Bài tập nâng cao

• Bài tập 3: Một vật được ném từ một vách đá cao 50 m với vận tốc ban đầu \(v_0 = 30 \, \text{m/s}\) theo phương xiên góc \( \theta = 60^\circ \). Tính thời gian bay và khoảng cách từ chân vách đá đến điểm vật chạm đất.

  Giải: Sử dụng các công thức và phương trình:

  • Thời gian bay: \( T = \frac{v_0 \sin \theta + \sqrt{(v_0 \sin \theta)^2 + 2gh}}{g} \)
  • Khoảng cách: \( x = v_0 \cos \theta \times T \)

6.3. Các lỗi thường gặp và cách khắc phục

• Lỗi 1: Không tính đến lực cản không khí.

  Cách khắc phục: Trong các bài tập nâng cao hoặc thực tế, cần xem xét lực cản không khí để có kết quả chính xác hơn.

• Lỗi 2: Nhầm lẫn giữa các góc trong tính toán.

  Cách khắc phục: Luôn kiểm tra lại các góc trong quá trình tính toán và sử dụng công cụ hỗ trợ như máy tính hoặc phần mềm mô phỏng.

Chuyển động ném xiên là một loại chuyển động hai chiều phổ biến trong vật lý. Để hiểu rõ hơn về hiện tượng này, chúng ta có thể phân tích chuyển động thành hai thành phần: chuyển động theo phương nằm ngang và chuyển động theo phương thẳng đứng. Mỗi thành phần này tuân theo các quy luật cơ bản của động lực học, và sự kết hợp của chúng tạo thành quỹ đạo parabol đặc trưng của chuyển động ném xiên.

• Thành phần theo phương ngang:

  Chuyển động theo phương ngang có vận tốc không đổi vì không có lực nào tác động lên vật theo phương này (nếu bỏ qua sức cản không khí). Vận tốc theo phương ngang được xác định bởi công thức:

  \[
  v_x = v_0 \cdot \cos(\alpha)
  \]

• Thành phần theo phương thẳng đứng:

  Chuyển động theo phương thẳng đứng là một chuyển động rơi tự do với gia tốc trọng trường \(g\) và vận tốc ban đầu theo phương này là:

  \[
  v_y = v_0 \cdot \sin(\alpha) - g \cdot t
  \]

  Trong đó, \(v_0\) là vận tốc ban đầu và \(\alpha\) là góc ném so với phương ngang.

Khi phân tích cụ thể hơn, chúng ta có thể tính toán các thông số quan trọng của chuyển động ném xiên, bao gồm:

1. Thời gian bay:

   Thời gian bay của vật cho đến khi chạm đất được xác định bằng cách giải phương trình chuyển động theo phương thẳng đứng:

   \[
   t = \frac{2 \cdot v_0 \cdot \sin(\alpha)}{g}
   \]

2. Tầm xa:

   Tầm xa của chuyển động ném xiên là khoảng cách lớn nhất mà vật có thể đạt được theo phương ngang, được tính bằng công thức:

   \[
   L = \frac{v_0^2 \cdot \sin(2\alpha)}{g}
   \]

3. Tầm cao:

   Tầm cao của chuyển động là độ cao lớn nhất mà vật có thể đạt được, được xác định bởi công thức:

   \[
   H = \frac{v_0^2 \cdot \sin^2(\alpha)}{2g}
   \]

Như vậy, việc phân tích chuyển động ném xiên giúp chúng ta hiểu rõ hơn về quỹ đạo và các yếu tố ảnh hưởng đến chuyển động này. Qua đó, có thể ứng dụng trong nhiều lĩnh vực khác nhau như thể thao, quân sự và kỹ thuật.