Chuyển động ném ngang: Khám phá chi tiết và ứng dụng trong thực tế

Chuyển động ném ngang là một dạng chuyển động quan trọng trong cơ học vật lý. Đặc trưng của chuyển động này là một vật được ném theo phương ngang với vận tốc ban đầu, sau đó chịu tác động của trọng lực theo phương thẳng đứng.

Các phương trình cơ bản

Phương trình chuyển động ném ngang có thể được mô tả bởi hai thành phần:

• Chuyển động theo phương ngang (Ox): Vật di chuyển với vận tốc không đổi \( v_0 \).
• Chuyển động theo phương thẳng đứng (Oy): Vật chịu tác động của gia tốc trọng trường \( g \), tạo ra chuyển động biến đổi đều.

Phương trình chuyển động

Giả sử vật được ném ngang từ độ cao \( h \) với vận tốc ban đầu \( v_0 \), các phương trình quỹ đạo và thời gian rơi được tính như sau:

Phương trình quỹ đạo:

Phương trình quỹ đạo của vật là:

Trong đó:

• \( y \): độ cao của vật so với điểm ném
• \( x \): khoảng cách vật di chuyển theo phương ngang
• \( g \): gia tốc trọng trường, thường lấy \( g \approx 9,8 m/s^2 \)

Thời gian để vật chạm đất được tính bằng công thức:

Trong đó:

• \( h \): độ cao của điểm ném so với mặt đất

Ví dụ tính toán

Giả sử một vật được ném ngang với vận tốc \( v_0 = 10 \, \text{m/s} \) từ độ cao \( h = 20 \, \text{m} \). Ta có:

• Thời gian rơi:
\[ t = \sqrt{\frac{2 \times 20}{9,8}} \approx 2,02 \, \text{giây} \]
• Tầm xa của vật:
\[ x = v_0 \times t = 10 \times 2,02 = 20,2 \, \text{m} \]

Các yếu tố ảnh hưởng đến chuyển động ném ngang

• Vận tốc ban đầu: Vận tốc càng lớn thì tầm xa của vật càng lớn.
• Độ cao điểm ném: Độ cao càng lớn thì thời gian rơi càng dài, và do đó, tầm xa cũng tăng.
• Sức cản của không khí: Nếu bỏ qua sức cản không khí, vật sẽ chuyển động theo quỹ đạo parabol.

Ứng dụng của chuyển động ném ngang

• Chuyển động ném ngang có thể được ứng dụng trong nhiều lĩnh vực thực tế như thể thao (ném bóng, bắn cung), quân sự (bắn đạn pháo), và nghiên cứu khoa học.
• Các bài toán liên quan đến chuyển động ném ngang thường xuất hiện trong chương trình học vật lý cấp phổ thông và được sử dụng để rèn luyện kỹ năng giải toán và phân tích chuyển động.

Chuyển động ném ngang là một loại chuyển động trong cơ học, được mô tả bởi một vật thể được ném theo phương ngang với một vận tốc ban đầu. Trong quá trình chuyển động, vật thể chịu tác động của trọng lực làm cho quỹ đạo của nó trở thành một đường cong.

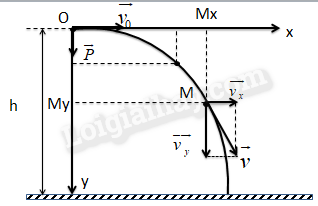
• Về mặt toán học, chuyển động ném ngang được xem là sự kết hợp của hai chuyển động riêng rẽ: chuyển động đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng.
• Phương trình chuyển động ngang có dạng: \[ x = v_0 \cdot t \] với \( v_0 \) là vận tốc ban đầu theo phương ngang.
• Chuyển động theo phương thẳng đứng chịu tác động của gia tốc trọng trường: \[ y = \frac{1}{2} g \cdot t^2 \] trong đó \( g \) là gia tốc trọng trường, và \( t \) là thời gian chuyển động.

Nhờ sự kết hợp của hai chuyển động này, quỹ đạo của vật ném ngang là một parabol trong mặt phẳng thẳng đứng.

Phương trình chuyển động ném ngang được xây dựng dựa trên hai chuyển động chính: chuyển động đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng. Sự kết hợp này tạo nên quỹ đạo parabol đặc trưng của chuyển động ném ngang.

• Phương ngang: Vật chuyển động theo phương ngang với vận tốc ban đầu \( v_0 \), không bị tác động bởi lực nào khác ngoài lực ban đầu. Phương trình tọa độ theo thời gian: \[ x = v_0 \cdot t \] Trong đó:
  • \( x \): Quãng đường đi theo phương ngang
  • \( v_0 \): Vận tốc ban đầu theo phương ngang
  • \( t \): Thời gian chuyển động
• Phương thẳng đứng: Vật chịu tác động của trọng lực với gia tốc \( g \) theo phương thẳng đứng. Phương trình theo thời gian của tọa độ thẳng đứng: \[ y = \frac{1}{2} g \cdot t^2 \] Trong đó:
  • \( y \): Quãng đường rơi theo phương thẳng đứng
  • \( g \): Gia tốc trọng trường (thường là \( 9,8 \, m/s^2 \))
  • \( t \): Thời gian chuyển động
• Quỹ đạo parabol: Từ hai phương trình trên, ta có thể xây dựng phương trình quỹ đạo của chuyển động ném ngang: \[ y = \frac{g}{2v_0^2} \cdot x^2 \] Đây là phương trình của một parabol trong mặt phẳng thẳng đứng.

Chuyển động ném ngang bao gồm nhiều công thức quan trọng giúp mô tả quá trình chuyển động của vật thể. Dưới đây là các công thức cơ bản cần nắm vững:

• Công thức tính quãng đường theo phương ngang: Vật thể chuyển động đều theo phương ngang với vận tốc không đổi \( v_0 \). \[ x = v_0 \cdot t \] Trong đó:
  • \( x \): Quãng đường theo phương ngang (m)
  • \( v_0 \): Vận tốc ban đầu theo phương ngang (m/s)
  • \( t \): Thời gian chuyển động (s)
• Công thức tính quãng đường theo phương thẳng đứng: Vật rơi tự do dưới tác dụng của trọng lực với gia tốc \( g \). \[ y = \frac{1}{2} g \cdot t^2 \] Trong đó:
  • \( y \): Quãng đường theo phương thẳng đứng (m)
  • \( g \): Gia tốc trọng trường (thường là \( 9,8 \, m/s^2 \))
  • \( t \): Thời gian rơi tự do (s)
• Công thức thời gian rơi: Thời gian vật thể rơi từ độ cao \( h \) được xác định bằng: \[ t = \sqrt{\frac{2h}{g}} \] Trong đó:
  • \( t \): Thời gian rơi (s)
  • \( h \): Độ cao ban đầu (m)
  • \( g \): Gia tốc trọng trường (m/s²)
• Phương trình quỹ đạo: Sự kết hợp của hai phương trình chuyển động tạo ra phương trình quỹ đạo của vật thể: \[ y = \frac{g}{2v_0^2} \cdot x^2 \] Đây là phương trình của một parabol trong mặt phẳng thẳng đứng.

Chuyển động ném ngang là dạng bài tập thường gặp trong các bài kiểm tra Vật lý. Dưới đây là một ví dụ bài tập điển hình về chuyển động ném ngang cùng các bước giải chi tiết:

Ví dụ: Một vật được ném ngang từ độ cao 20m so với mặt đất với vận tốc ban đầu \( v_0 = 5 \, m/s \). Bỏ qua lực cản không khí. Hãy xác định:

1. Thời gian vật rơi chạm đất.
2. Quãng đường vật đi được theo phương ngang.

Lời giải:

• Bước 1: Tính thời gian vật rơi theo phương thẳng đứng: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \cdot 20}{9.8}} \approx 2.02 \, s \] Trong đó:
  • \( h \) là độ cao (20m)
  • \( g \) là gia tốc trọng trường (\( 9.8 \, m/s^2 \))
  • \( t \) là thời gian rơi
• Bước 2: Tính quãng đường vật đi được theo phương ngang: \[ x = v_0 \cdot t = 5 \cdot 2.02 \approx 10.1 \, m \] Trong đó:
  • \( v_0 \) là vận tốc ban đầu theo phương ngang (5 m/s)
  • \( t \) là thời gian rơi đã tính được ở Bước 1

Kết luận: Vật rơi chạm đất sau khoảng thời gian 2.02 giây và di chuyển được quãng đường 10.1 mét theo phương ngang.

Chuyển động ném ngang không chỉ là một khái niệm trong Vật lý mà còn được áp dụng rộng rãi trong nhiều lĩnh vực của đời sống và kỹ thuật. Các ứng dụng bao gồm từ thể thao, quân sự cho đến hàng không vũ trụ. Dưới đây là một số ví dụ về ứng dụng thực tế của chuyển động ném ngang:

• Trong thể thao: Các vận động viên bóng đá, bóng chày, bóng rổ thường áp dụng kiến thức về chuyển động ném ngang để tối ưu hóa đường bay của bóng, giúp nó đến đích chính xác.
• Trong quân sự: Các vũ khí như súng và pháo sử dụng nguyên lý chuyển động ném ngang để tính toán đường đạn, từ đó xác định tầm bắn và góc bắn tối ưu.
• Trong hàng không vũ trụ: Khi phóng vệ tinh hoặc tên lửa, các kỹ sư cần tính toán chính xác chuyển động ném ngang để đưa vật thể vào quỹ đạo.

Qua các ứng dụng này, có thể thấy chuyển động ném ngang là một phần không thể thiếu trong việc phát triển công nghệ và nâng cao hiệu suất trong nhiều lĩnh vực khác nhau.

Dưới đây là một số bài tập vận dụng và mở rộng giúp bạn hiểu sâu hơn về chuyển động ném ngang. Các bài tập này yêu cầu áp dụng các công thức đã học và mở rộng thêm về các tình huống thực tế khác nhau.

1. Bài tập 1: Một vật được ném ngang từ độ cao \( h = 20 \, \text{m} \) với vận tốc ban đầu \( v_0 = 10 \, \text{m/s} \). Tính thời gian vật chạm đất và tầm xa của vật.
2. Bài tập 2: Một vận động viên bóng rổ ném bóng theo phương ngang từ độ cao \( h = 3 \, \text{m} \) với vận tốc ban đầu \( v_0 = 8 \, \text{m/s} \). Tính khoảng cách bóng rơi xuống mặt đất.
3. Bài tập mở rộng: Một viên đạn được bắn theo phương ngang với vận tốc \( v_0 = 500 \, \text{m/s} \) từ độ cao \( h = 50 \, \text{m} \). Tính thời gian bay và khoảng cách viên đạn chạm đất, giả sử không có lực cản của không khí.

Các bài tập này giúp học sinh vừa rèn luyện kỹ năng tính toán, vừa liên hệ đến những ứng dụng thực tế của chuyển động ném ngang.