Chủ đề chuyển động nhanh dần: Chuyển động nhanh dần là một hiện tượng quan trọng trong vật lý, giúp chúng ta hiểu rõ hơn về cách các vật thể tăng tốc trong không gian. Bài viết này sẽ khám phá chi tiết khái niệm, các công thức cơ bản, và những ứng dụng thực tiễn của chuyển động nhanh dần trong đời sống hàng ngày.
Mục lục
Chuyển Động Nhanh Dần
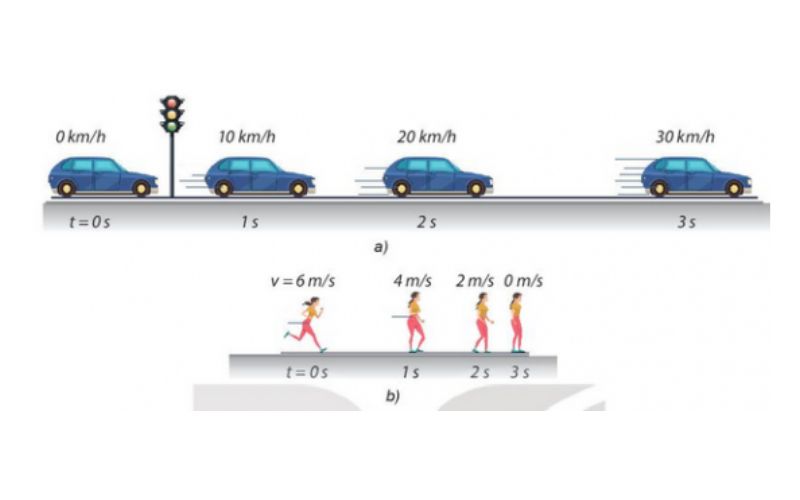
Chuyển động nhanh dần là một loại chuyển động trong đó vận tốc của vật tăng dần theo thời gian. Đây là một hiện tượng phổ biến trong đời sống và có ứng dụng rộng rãi trong nhiều lĩnh vực, từ vật lý cơ bản đến các ngành công nghiệp kỹ thuật.
1. Định nghĩa và đặc điểm
Chuyển động nhanh dần là chuyển động có gia tốc dương, nghĩa là vận tốc của vật tăng lên theo thời gian. Gia tốc trong chuyển động nhanh dần được xác định bởi công thức:
\[ a = \frac{\Delta v}{\Delta t} \]
Trong đó:
- \( a \): Gia tốc (m/s²)
- \( \Delta v \): Độ biến thiên vận tốc (m/s)
- \( \Delta t \): Thời gian (s)
Nếu gia tốc \( a > 0 \), vật sẽ chuyển động nhanh dần. Nếu gia tốc \( a < 0 \), vật chuyển động chậm dần.
2. Phương trình chuyển động nhanh dần
Phương trình chuyển động nhanh dần đều được mô tả bởi các công thức sau:
\[ v = v_0 + at \]
\[ s = v_0t + \frac{1}{2}at^2 \]
Trong đó:
- \( v \): Vận tốc tức thời (m/s)
- \( v_0 \): Vận tốc ban đầu (m/s)
- \( t \): Thời gian (s)
- \( s \): Quãng đường đi được (m)
3. Ứng dụng của chuyển động nhanh dần
Chuyển động nhanh dần có nhiều ứng dụng trong các ngành công nghiệp và đời sống hàng ngày:
- Trong sản xuất ô tô, chuyển động nhanh dần được ứng dụng trong thiết kế hệ thống tăng tốc và phanh.
- Trong các ngành xây dựng và giao thông, tính toán chuyển động nhanh dần giúp đảm bảo an toàn và hiệu suất trong các dự án cầu đường và tàu điện.
- Chuyển động nhanh dần cũng được nghiên cứu trong lĩnh vực thể thao để tối ưu hóa hiệu suất của các vận động viên trong các môn đua xe và điền kinh.
4. Bài tập ví dụ
Ví dụ: Một ô tô ban đầu đứng yên, sau 5 giây chuyển động nhanh dần đều với gia tốc 2 m/s². Hỏi quãng đường ô tô đi được trong thời gian đó là bao nhiêu?
Lời giải:
Sử dụng công thức:
\[ s = v_0t + \frac{1}{2}at^2 \]
Vì \( v_0 = 0 \), ta có:
\[ s = \frac{1}{2} \times 2 \times 5^2 = 25 \text{m} \]
Vậy quãng đường ô tô đi được là 25 mét.
5. Tổng kết
Chuyển động nhanh dần là một hiện tượng vật lý quan trọng với nhiều ứng dụng thực tế. Nó giúp chúng ta hiểu rõ hơn về cách vật thể di chuyển và biến đổi vận tốc trong các môi trường khác nhau.

.png)
1. Khái niệm về chuyển động nhanh dần
Chuyển động nhanh dần là một dạng chuyển động thẳng biến đổi đều, trong đó vận tốc của vật tăng dần theo thời gian. Đặc trưng của chuyển động này là gia tốc \(a > 0\), được định nghĩa là tỉ số giữa độ biến thiên vận tốc \(\Delta v\) và khoảng thời gian biến thiên \(\Delta t\). Công thức tính gia tốc:
- \[a = \frac{\Delta v}{\Delta t}\]
Trong chuyển động nhanh dần, quãng đường đi được \(s\) của vật sau khoảng thời gian \(t\) được xác định bằng công thức:
- \[s = v_0 t + \frac{1}{2} a t^2\]
Trong đó, \(v_0\) là vận tốc ban đầu của vật, và \(a\) là gia tốc không đổi.
2. Các công thức cơ bản
Trong chuyển động nhanh dần đều, có một số công thức cơ bản thường được sử dụng để tính toán các đại lượng như vận tốc, gia tốc, và quãng đường. Những công thức này giúp xác định chính xác trạng thái chuyển động của vật thể khi gia tốc không đổi. Dưới đây là các công thức cơ bản liên quan:
- Vận tốc tức thời \[v = v_0 + a \cdot t\], trong đó:
- \(v\) là vận tốc tại thời điểm \(t\)
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc không đổi
- \(t\) là thời gian
- Quãng đường đi được \[s = v_0 \cdot t + \frac{1}{2} a \cdot t^2\], trong đó:
- \(s\) là quãng đường đi được
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc
- \(t\) là thời gian
- Công thức liên hệ giữa vận tốc và quãng đường \[v^2 = v_0^2 + 2a \cdot s\], trong đó:
- \(v\) là vận tốc tức thời
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc
- \(s\) là quãng đường đi được
Những công thức này được sử dụng để giải quyết các bài toán chuyển động, từ tính toán gia tốc, quãng đường đến vận tốc của vật trong suốt quá trình chuyển động nhanh dần đều.

3. Đồ thị vận tốc - thời gian
Đồ thị vận tốc - thời gian của chuyển động nhanh dần đều là một đường thẳng dốc lên, thể hiện vận tốc của vật tăng dần theo thời gian. Điều này có nghĩa là gia tốc của vật là một hằng số và được biểu diễn bằng độ dốc của đường thẳng này.
Khi xét đồ thị vận tốc - thời gian, trục hoành (trục x) đại diện cho thời gian (\(t\)) và trục tung (trục y) đại diện cho vận tốc (\(v\)). Đồ thị có dạng:
Trong đó:
- \(v(t)\): Vận tốc của vật tại thời điểm \(t\)
- \(v_0\): Vận tốc ban đầu của vật
- \(a\): Gia tốc của vật (đại lượng không đổi)
- \(t\): Thời gian
Độ dốc của đường thẳng trên đồ thị cho ta biết gia tốc của vật. Nếu gia tốc dương (\(a > 0\)), đồ thị có độ dốc lên, biểu thị chuyển động nhanh dần. Ngược lại, nếu gia tốc âm (\(a < 0\)), đồ thị sẽ có độ dốc xuống, tương ứng với chuyển động chậm dần.
Dựa vào diện tích phía dưới đường thẳng, ta có thể tính được quãng đường mà vật di chuyển được trong khoảng thời gian đã xét, với công thức tính quãng đường:
Đồ thị vận tốc - thời gian là một công cụ quan trọng để phân tích sự thay đổi vận tốc và quãng đường của vật trong chuyển động nhanh dần đều.
4. Các bài toán vận dụng thực tế
Trong thực tế, các bài toán chuyển động nhanh dần đều thường xuất hiện trong các tình huống liên quan đến giao thông, kỹ thuật, và đời sống hàng ngày. Việc ứng dụng các công thức chuyển động nhanh dần đều giúp giải quyết các bài toán liên quan đến quãng đường, vận tốc và gia tốc trong nhiều bối cảnh khác nhau.
- Giao thông: Tính toán quãng đường ô tô di chuyển sau khi bắt đầu tăng tốc hoặc giảm tốc là một ứng dụng điển hình. Ví dụ, khi một ô tô tăng tốc với một gia tốc đều, ta có thể sử dụng công thức để tính quãng đường đi được sau một thời gian nhất định.
- Kỹ thuật: Trong kỹ thuật cơ khí, các bài toán liên quan đến chuyển động của máy móc, thiết bị như thang máy, robot công nghiệp đều liên quan đến các tính toán vận tốc và gia tốc để tối ưu hóa hoạt động.
- Thể thao: Trong môn chạy nước rút, các vận động viên cần duy trì một gia tốc ổn định trong giai đoạn đầu để đạt vận tốc tối đa. Bài toán tính thời gian, quãng đường và gia tốc trong thể thao giúp tối ưu hóa phương pháp tập luyện và thi đấu.
Những bài toán này đòi hỏi sự hiểu biết sâu sắc về các công thức chuyển động cơ bản và cách áp dụng chúng vào tình huống cụ thể. Chẳng hạn:
| Thời gian (s) | Vận tốc ban đầu (m/s) | Gia tốc (m/s²) | Quãng đường (m) |
|---|---|---|---|
| 5 | 0 | 2 | 25 |
| 10 | 0 | 3 | 150 |
Ví dụ này minh họa rõ ràng cách tính quãng đường của một vật chuyển động nhanh dần đều dựa trên các tham số như thời gian và gia tốc.

5. Ứng dụng thực tiễn của chuyển động nhanh dần
Chuyển động nhanh dần đều có ứng dụng rộng rãi trong nhiều lĩnh vực đời sống và công nghiệp. Các ứng dụng này không chỉ giúp cải thiện hiệu suất công việc mà còn tối ưu hóa các quy trình sản xuất và nâng cao độ an toàn trong giao thông và kỹ thuật. Dưới đây là một số ứng dụng thực tiễn nổi bật:
- Giao thông: Trong thiết kế hệ thống phanh và gia tốc của ô tô, chuyển động nhanh dần giúp tính toán chính xác quãng đường và thời gian cần thiết để dừng xe hoặc tăng tốc an toàn. Điều này góp phần cải thiện hiệu suất lái xe và giảm nguy cơ tai nạn giao thông.
- Kỹ thuật cơ khí: Các máy móc và thiết bị như thang máy, băng chuyền đều sử dụng chuyển động nhanh dần để di chuyển hàng hóa hoặc người một cách hiệu quả. Việc điều khiển tốc độ và gia tốc trong các thiết bị này giúp tiết kiệm năng lượng và giảm hao mòn thiết bị.
- Công nghệ vũ trụ: Chuyển động nhanh dần được áp dụng trong quá trình phóng tên lửa và các tàu vũ trụ. Từ khi rời khỏi mặt đất, các tên lửa phải gia tăng tốc độ dần dần để thoát khỏi lực hấp dẫn của Trái Đất, đòi hỏi sự tính toán kỹ lưỡng về gia tốc và vận tốc.
- Thể thao: Trong nhiều môn thể thao như điền kinh, việc tối ưu hóa gia tốc của vận động viên là yếu tố quyết định thành tích. Chuyển động nhanh dần giúp tính toán thời gian tăng tốc và giữ tốc độ tối đa để đạt được hiệu suất cao nhất.
Chính nhờ sự ứng dụng đa dạng này, chuyển động nhanh dần đều đã trở thành một phần quan trọng trong cuộc sống hiện đại, giúp tối ưu hóa các quy trình sản xuất và nâng cao sự an toàn trong nhiều lĩnh vực khác nhau.
XEM THÊM:
6. Các tài liệu và nghiên cứu liên quan
Trong quá trình học tập và nghiên cứu về chuyển động nhanh dần, có rất nhiều tài liệu hữu ích giúp củng cố kiến thức. Dưới đây là một số tài liệu và nghiên cứu quan trọng liên quan đến chủ đề này:
6.1. Sách giáo khoa Vật lý 10
Sách giáo khoa Vật lý lớp 10 là tài liệu căn bản cung cấp những khái niệm và công thức cơ bản về chuyển động nhanh dần. Trong sách, học sinh sẽ tìm thấy các công thức quan trọng như:
- Gia tốc: \( a = \frac{{\Delta v}}{{\Delta t}} \)
- Vận tốc: \( v = v_0 + at \)
- Quãng đường: \( s = v_0t + \frac{1}{2}a t^2 \)
Ngoài ra, sách còn cung cấp các bài tập vận dụng để học sinh rèn luyện kỹ năng tính toán và vẽ đồ thị liên quan đến chuyển động nhanh dần đều.
6.2. Các tài liệu tham khảo học thuật
Ngoài sách giáo khoa, có nhiều tài liệu nghiên cứu chuyên sâu giúp học sinh và sinh viên nắm rõ hơn về lý thuyết và ứng dụng của chuyển động nhanh dần. Một số tài liệu nổi bật bao gồm:
- Cơ học Newton và ứng dụng - Đây là một tài liệu học thuật chuyên sâu giải thích chi tiết các nguyên lý về chuyển động nhanh dần, dựa trên định luật thứ hai của Newton.
- Giáo trình Vật lý Đại cương - Tài liệu này cung cấp các bài tập nâng cao liên quan đến chuyển động nhanh dần, từ những bài toán cơ bản đến những tình huống phức tạp hơn như chuyển động trên mặt phẳng nghiêng.
- Các nghiên cứu về ứng dụng chuyển động trong kỹ thuật - Các nghiên cứu này tập trung vào việc áp dụng lý thuyết chuyển động nhanh dần trong các ngành như giao thông, kỹ thuật hàng không và cơ học kỹ thuật.
6.3. Các bài nghiên cứu khoa học
Trên các tạp chí khoa học, có rất nhiều bài báo nghiên cứu về chuyển động nhanh dần và các ứng dụng thực tiễn của nó. Một số nghiên cứu đáng chú ý bao gồm:
- Nghiên cứu về gia tốc trong chuyển động vật thể: Nghiên cứu này tập trung vào phân tích sự thay đổi gia tốc và cách tính toán quãng đường di chuyển trong các tình huống thực tiễn.
- Ứng dụng chuyển động nhanh dần trong công nghệ ô tô: Bài nghiên cứu này chỉ ra cách chuyển động nhanh dần được ứng dụng trong việc tăng tốc và phanh xe, đồng thời cải thiện hiệu suất an toàn giao thông.
Những tài liệu và nghiên cứu trên không chỉ giúp hiểu sâu hơn về chuyển động nhanh dần mà còn mở ra những hướng nghiên cứu và ứng dụng thực tiễn trong đời sống và kỹ thuật.