Công Thức Chuyển Động Ném Ngang: Hướng Dẫn Chi Tiết và Ứng Dụng Thực Tế

Chuyển động ném ngang là một dạng chuyển động thường gặp trong vật lý, đặc biệt là trong các bài học về động lực học. Đây là chuyển động của một vật bị ném theo phương ngang dưới tác dụng của trọng lực.

1. Định nghĩa chuyển động ném ngang

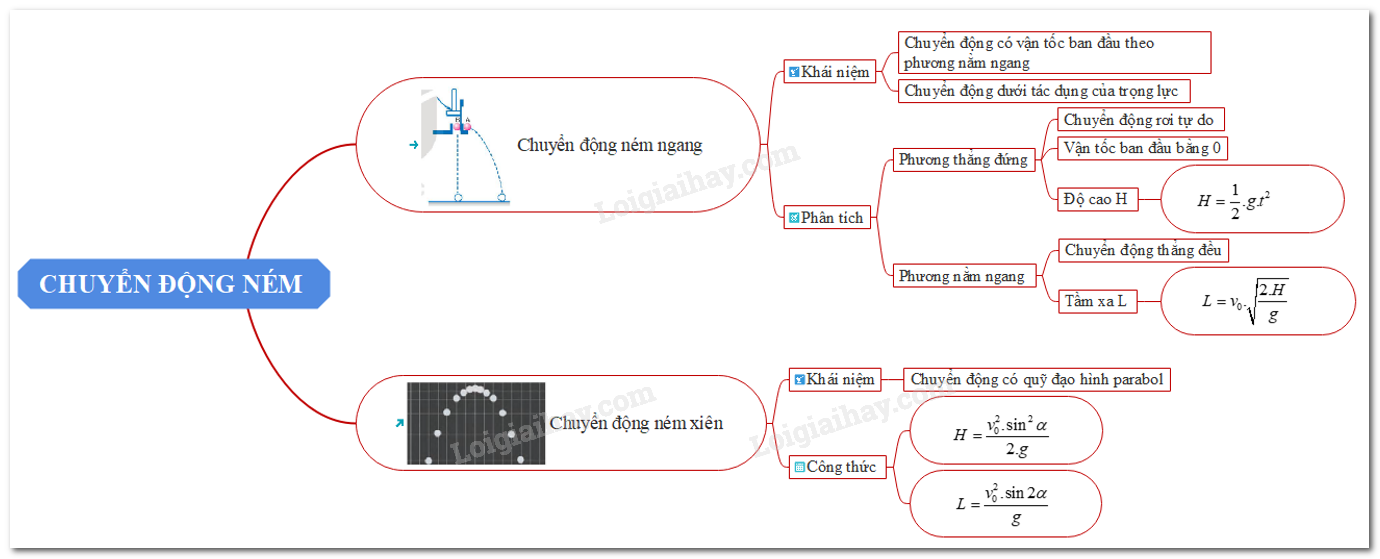
Chuyển động ném ngang là sự kết hợp giữa chuyển động thẳng đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng. Khi bỏ qua sức cản của không khí, quỹ đạo của vật sẽ là một đường parabol.

2. Các thành phần của chuyển động ném ngang

• Chuyển động theo phương ngang: Chuyển động này là chuyển động thẳng đều với vận tốc ban đầu \(v_0\) không đổi. Công thức tính độ dịch chuyển theo phương ngang là:
• \[ d_x = v_0 \cdot t \]
• Chuyển động theo phương thẳng đứng: Chuyển động này là chuyển động rơi tự do với gia tốc trọng trường \(g\). Độ cao của vật tại thời điểm \(t\) được tính theo công thức:
• \[ H = \frac{1}{2} g t^2 \]

3. Công thức tính thời gian rơi

Thời gian rơi của vật phụ thuộc vào độ cao ban đầu \(H\) và gia tốc trọng trường \(g\), được xác định bằng công thức:

4. Công thức tính tầm xa của chuyển động ném ngang

Tầm xa \(L\) là khoảng cách mà vật đi được theo phương ngang trước khi chạm đất, được tính bằng công thức:

5. Các yếu tố ảnh hưởng đến chuyển động ném ngang

• Vận tốc ban đầu \(v_0\): Tốc độ ném ban đầu càng lớn, tầm xa của chuyển động ném ngang càng dài.
• Độ cao \(H\): Vật ném từ độ cao càng lớn, thời gian rơi càng lâu và tầm xa càng lớn.
• Gia tốc trọng trường \(g\): Trong điều kiện thông thường, giá trị \(g\) được xem là không đổi (khoảng \(9.8 m/s^2\)).

6. Ứng dụng thực tế

Công thức chuyển động ném ngang được áp dụng trong nhiều lĩnh vực như kỹ thuật, quân sự, thể thao, và nhiều thí nghiệm vật lý. Ví dụ, việc tính toán quỹ đạo của một viên đạn, hoặc xác định tầm ném xa của một cầu thủ trong môn bóng rổ.

• 1. Định Nghĩa và Khái Quát Về Chuyển Động Ném Ngang
  • 1.1 Chuyển động ném ngang là gì?
  • 1.2 Các yếu tố ảnh hưởng đến chuyển động ném ngang
• 2. Công Thức Cơ Bản Trong Chuyển Động Ném Ngang
  • 2.1 Công thức tính tầm xa \( S = v_0 \times t \)
  • 2.2 Công thức tính thời gian chuyển động \( t = \sqrt{\frac{2h}{g}} \)
  • 2.3 Công thức tính độ cao rơi \( h = \frac{1}{2}gt^2 \)
• 3. Phân Tích Chuyển Động Ném Ngang
  • 3.1 Chuyển động theo phương ngang
  • 3.2 Chuyển động theo phương thẳng đứng
  • 3.3 Quỹ đạo của vật trong chuyển động ném ngang
• 4. Ứng Dụng Thực Tế Của Chuyển Động Ném Ngang
  • 4.1 Ứng dụng trong kỹ thuật và công nghệ
  • 4.2 Ứng dụng trong thể thao và giải trí
  • 4.3 Ứng dụng trong các thí nghiệm vật lý
• 5. Các Bài Tập Thực Hành Về Chuyển Động Ném Ngang
  • 5.1 Bài tập cơ bản: Tính tầm xa và thời gian rơi
  • 5.2 Bài tập nâng cao: Phân tích quỹ đạo và ứng dụng thực tế

Chuyển động ném ngang là một dạng chuyển động của vật thể trong không gian, trong đó vật được ném theo phương ngang với vận tốc ban đầu \(v_0\) và đồng thời chịu tác dụng của trọng lực \(g\) theo phương thẳng đứng. Trong quá trình này, vật sẽ chuyển động theo hai phương: phương ngang với vận tốc không đổi và phương thẳng đứng với gia tốc không đổi do trọng lực gây ra.

Đặc điểm chính của chuyển động ném ngang:

• 1.1 Chuyển động theo phương ngang: Trong suốt quá trình, vận tốc của vật theo phương ngang là không đổi và bằng với vận tốc ban đầu \(v_0\). Công thức tính quãng đường theo phương ngang là: \[ S = v_0 \times t \] trong đó \(t\) là thời gian chuyển động.
• 1.2 Chuyển động theo phương thẳng đứng: Vật chịu tác dụng của trọng lực và rơi tự do theo phương thẳng đứng. Gia tốc theo phương này là \(g\), và quãng đường rơi được tính theo công thức: \[ h = \frac{1}{2}gt^2 \].
• 1.3 Quỹ đạo chuyển động: Quỹ đạo của chuyển động ném ngang là một đường parabol, kết hợp giữa chuyển động thẳng đều theo phương ngang và chuyển động thẳng biến đổi đều theo phương thẳng đứng.

Trong chuyển động ném ngang, các công thức cơ bản giúp ta mô tả quỹ đạo và vận tốc của vật thể khi nó chuyển động dưới tác động của trọng lực. Các công thức này kết hợp chuyển động theo hai phương: phương ngang (không chịu tác động của lực) và phương thẳng đứng (chịu tác động của trọng lực).

• 2.1 Công thức tính thời gian bay:

  Thời gian bay \(t\) của vật được xác định bằng công thức: \[ t = \sqrt{\frac{2h}{g}} \] trong đó:

  • \(h\) là độ cao ban đầu của vật khi bắt đầu ném.
  • \(g\) là gia tốc trọng trường (khoảng 9,8 m/s²).
• 2.2 Công thức tính quãng đường theo phương ngang:

  Quãng đường theo phương ngang \(S\) mà vật di chuyển được trong thời gian bay \(t\) là: \[ S = v_0 \times t \] trong đó:

  • \(v_0\) là vận tốc ban đầu theo phương ngang.
• 2.3 Công thức tính vận tốc của vật tại thời điểm bất kỳ:

  Vận tốc của vật tại thời điểm bất kỳ trong chuyển động ném ngang được tính bằng cách kết hợp vận tốc theo phương ngang và phương thẳng đứng: \[ v = \sqrt{v_0^2 + (gt)^2} \] trong đó:

  • \(v_0\) là vận tốc ban đầu theo phương ngang.
  • \(g\) là gia tốc trọng trường.
  • \(t\) là thời gian kể từ khi bắt đầu chuyển động.

Chuyển động ném ngang là một dạng chuyển động trong không gian hai chiều, trong đó một vật được ném với vận tốc ban đầu theo phương ngang và bị tác động bởi lực trọng trường theo phương thẳng đứng. Để phân tích chuyển động này, ta cần xem xét riêng lẻ từng thành phần của chuyển động theo hai phương: phương ngang và phương thẳng đứng.

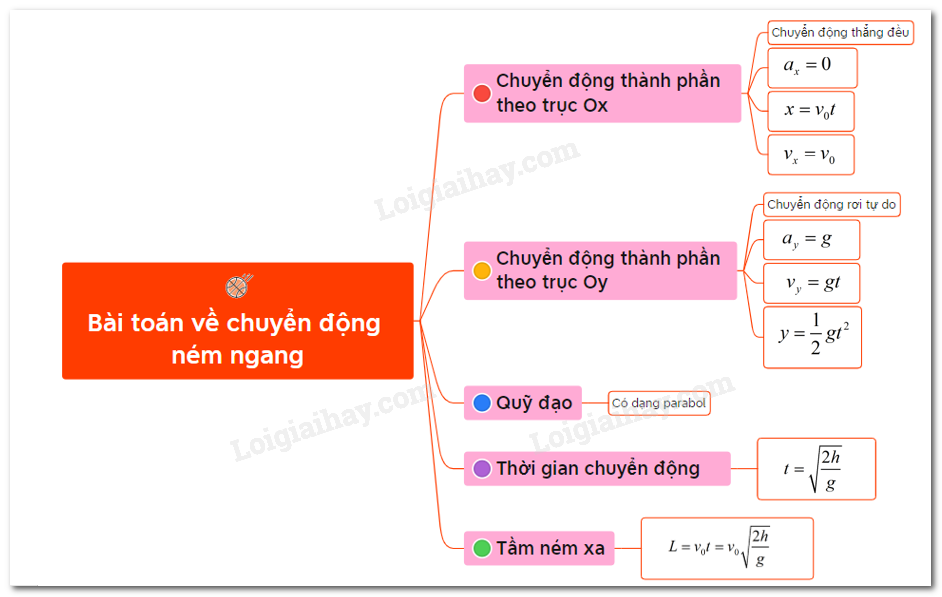
• 3.1 Phân tích chuyển động theo phương ngang:

  Vận tốc theo phương ngang \(v_x\) của vật là không đổi do không có lực tác dụng theo phương này. Quãng đường theo phương ngang \(S_x\) được tính theo công thức:

  \[ S_x = v_0 \times t \]

  trong đó \(v_0\) là vận tốc ban đầu theo phương ngang và \(t\) là thời gian chuyển động.

• 3.2 Phân tích chuyển động theo phương thẳng đứng:

  Theo phương thẳng đứng, vật chịu tác dụng của trọng lực nên chuyển động theo dạng rơi tự do. Vận tốc theo phương thẳng đứng \(v_y\) tại thời điểm \(t\) được tính bởi:

  \[ v_y = g \times t \]

  trong đó \(g\) là gia tốc trọng trường.

• 3.3 Phân tích quỹ đạo của chuyển động:

  Quỹ đạo của chuyển động ném ngang là một đường cong parabol, được xác định bởi phương trình:

  \[ y = \frac{1}{2}gt^2 \]

  trong đó \(y\) là độ cao so với vị trí ban đầu, \(g\) là gia tốc trọng trường, và \(t\) là thời gian.

• 3.4 Ứng dụng thực tế của phân tích chuyển động ném ngang:

  Phân tích chuyển động ném ngang được ứng dụng rộng rãi trong nhiều lĩnh vực như thể thao, quân sự, và khoa học vũ trụ. Hiểu rõ các nguyên lý này giúp chúng ta dự đoán và kiểm soát chuyển động của vật thể trong các điều kiện thực tế.

Chuyển động ném ngang là một nguyên lý quan trọng trong nhiều lĩnh vực khác nhau, từ thể thao đến quân sự và khoa học vũ trụ. Hiểu biết về chuyển động này giúp chúng ta áp dụng các công thức vật lý để tối ưu hóa kết quả trong thực tế.

• 4.1 Thể thao:

  Trong bóng đá, bóng rổ, và cầu lông, việc tính toán chính xác góc ném và vận tốc ban đầu của bóng giúp vận động viên đạt được đường ném tối ưu.

• 4.2 Quân sự:

  Chuyển động ném ngang được sử dụng để dự đoán quỹ đạo của đạn đạo hoặc các thiết bị phóng, từ đó tính toán chính xác điểm rơi và điều chỉnh hướng ném để đạt mục tiêu mong muốn.

• 4.3 Khoa học vũ trụ:

  Trong nghiên cứu vũ trụ, hiểu biết về chuyển động ném ngang giúp các nhà khoa học thiết kế quỹ đạo bay cho các vệ tinh hoặc tàu vũ trụ, đảm bảo rằng chúng có thể đạt được độ cao và tốc độ cần thiết để quay quanh Trái đất hoặc các thiên thể khác.

• 4.4 Ứng dụng trong đời sống:

  Trong đời sống hàng ngày, từ việc ném một vật nhẹ đến việc xây dựng các thiết bị giải trí như máy ném bóng, chuyển động ném ngang được ứng dụng để tạo ra các sản phẩm và dịch vụ phục vụ nhu cầu của con người.

Dưới đây là một số bài tập thực hành về chuyển động ném ngang nhằm giúp bạn hiểu rõ hơn về các công thức và cách áp dụng chúng trong thực tế:

5.1 Bài tập cơ bản về tính thời gian rơi và tầm xa

Bài tập 1: Một vật được ném ngang từ độ cao \( h = 20 \, \text{m} \) với vận tốc ban đầu \( v_0 = 15 \, \text{m/s} \). Tính thời gian rơi và tầm xa của vật.

1. Thời gian rơi của vật được tính bằng công thức: \[ t = \sqrt{\frac{2h}{g}} \] Trong đó, \( g = 9.8 \, \text{m/s}^2 \) là gia tốc trọng trường.
2. Thay số vào công thức: \[ t = \sqrt{\frac{2 \times 20}{9.8}} \approx 2.02 \, \text{giây} \]
3. Tầm xa của vật được tính bằng công thức: \[ L = v_0 \times t \]
4. Thay số vào công thức: \[ L = 15 \times 2.02 \approx 30.3 \, \text{m} \]

5.2 Bài tập nâng cao về phân tích quỹ đạo

Bài tập 2: Một vật được ném ngang với vận tốc ban đầu \( v_0 = 10 \, \text{m/s} \) từ độ cao \( h = 45 \, \text{m} \). Tính quãng đường vật đi được theo phương ngang khi vật chạm đất và mô tả quỹ đạo của vật.

1. Thời gian rơi của vật: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 45}{9.8}} \approx 3.03 \, \text{giây} \]
2. Quãng đường theo phương ngang: \[ L = v_0 \times t = 10 \times 3.03 \approx 30.3 \, \text{m} \]
3. Quỹ đạo của vật là một đường parabol với phương trình quỹ đạo: \[ y = \frac{g}{2v_0^2}x^2 \] Thay số để xác định hình dạng của quỹ đạo: \[ y = \frac{9.8}{2 \times 10^2}x^2 = \frac{0.49}{100}x^2 = 0.0049x^2 \]

5.3 Bài tập ứng dụng thực tế

Bài tập 3: Một người đứng trên một tòa nhà cao \( h = 60 \, \text{m} \) và ném một quả bóng theo phương ngang với vận tốc \( v_0 = 20 \, \text{m/s} \). Hãy tính khoảng cách từ chân tòa nhà đến điểm bóng chạm đất và thời gian bóng rơi.

1. Thời gian rơi của bóng: \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 60}{9.8}} \approx 3.5 \, \text{giây} \]
2. Khoảng cách từ chân tòa nhà đến điểm bóng chạm đất: \[ L = v_0 \times t = 20 \times 3.5 = 70 \, \text{m} \]

Qua các bài tập trên, chúng ta có thể thấy rõ mối liên hệ giữa các công thức trong chuyển động ném ngang và cách áp dụng chúng vào thực tế. Việc thực hành các bài tập này sẽ giúp bạn nắm vững hơn các khái niệm và phương pháp tính toán liên quan đến chuyển động ném ngang.