Ba điện tích q giống hệt nhau: Bài toán và ứng dụng trong điện học

Bài toán liên quan đến ba điện tích q giống hệt nhau là một bài tập phổ biến trong vật lý, đặc biệt trong các chương trình học tập về điện trường và lực tương tác giữa các điện tích. Trong bài toán này, ba điện tích q được đặt tại các đỉnh của một tam giác đều với độ lớn điện tích bằng nhau và khoảng cách giữa các đỉnh tam giác bằng nhau.

Cách giải bài toán

Để giải bài toán này, chúng ta cần sử dụng các công thức về cường độ điện trường và lực tương tác giữa các điện tích. Dưới đây là các bước cơ bản:

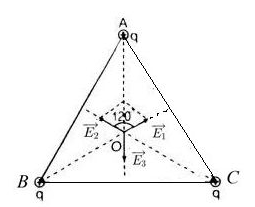
1. Xác định cường độ điện trường tại tâm của tam giác đều do mỗi điện tích gây ra. Cường độ điện trường tại tâm O do điện tích q đặt tại đỉnh A, B, C được tính như sau:

   
   \[
   E = k \cdot \frac{q}{{r^2}}
   \]

   Trong đó, \( r \) là khoảng cách từ tâm O đến mỗi đỉnh của tam giác đều, và \( k \) là hằng số điện môi.

2. Tính tổng hợp cường độ điện trường tại tâm O bằng cách cộng vectơ các cường độ điện trường do ba điện tích q gây ra.

   Do tam giác đều có tính đối xứng, các vectơ cường độ điện trường do hai điện tích đặt tại hai đỉnh đối diện sẽ triệt tiêu nhau. Vì vậy, tổng hợp cường độ điện trường tại O bằng 0:

   
   \[
   \overrightarrow{E_O} = \overrightarrow{E_1} + \overrightarrow{E_2} + \overrightarrow{E_3} = 0
   \]

3. Kết luận: Cường độ điện trường tại tâm của tam giác đều bằng 0. Điều này có nghĩa là các lực tương tác giữa các điện tích sẽ cân bằng nhau tại tâm của tam giác đều.

Ứng dụng của bài toán

Bài toán về ba điện tích q giống hệt nhau không chỉ có giá trị trong việc rèn luyện kỹ năng giải bài tập vật lý mà còn có ứng dụng trong việc hiểu rõ hơn về các hiện tượng tự nhiên, đặc biệt là trong lĩnh vực điện học và điện từ học.

Bài toán này cũng giúp học sinh làm quen với các phương pháp phân tích vectơ và các nguyên lý cân bằng lực trong các hệ thống điện tích, từ đó phát triển tư duy logic và khả năng giải quyết vấn đề.

Bài toán về ba điện tích q giống hệt nhau thường được đặt trong bối cảnh các điện tích này nằm tại các đỉnh của một tam giác đều. Đây là một bài toán điển hình trong chương trình vật lý, giúp học sinh hiểu rõ hơn về lực tương tác Coulomb và cường độ điện trường.

Để giải bài toán này, ta cần xác định lực tương tác giữa các điện tích và cường độ điện trường tổng hợp tại các vị trí đặc biệt như tâm tam giác. Bài toán này được giải quyết qua các bước cụ thể sau:

1. Xác định khoảng cách giữa các điện tích: Với tam giác đều có cạnh là \(a\), khoảng cách giữa các điện tích được tính là \(r = a\).
2. Tính lực tương tác giữa hai điện tích bất kỳ: Theo định luật Coulomb, lực tương tác giữa hai điện tích \(q_1\) và \(q_2\) đặt cách nhau một khoảng \(r\) được tính bằng công thức:

   
   \[
   F = k \cdot \frac{{|q_1 \cdot q_2|}}{{r^2}}
   \]

3. Tính cường độ điện trường tại tâm tam giác: Do tính đối xứng của tam giác đều, các cường độ điện trường do mỗi điện tích gây ra tại tâm tam giác sẽ triệt tiêu nhau, dẫn đến cường độ điện trường tổng hợp tại tâm bằng 0.

Bài toán này không chỉ giúp người học nắm vững các khái niệm cơ bản về điện trường và lực tương tác điện tích mà còn rèn luyện khả năng phân tích và giải quyết vấn đề phức tạp trong vật lý.

Dưới đây là một số ví dụ và bài tập liên quan đến bài toán ba điện tích q giống hệt nhau. Những bài tập này giúp củng cố kiến thức về lực tương tác Coulomb và cường độ điện trường, đồng thời rèn luyện khả năng giải quyết vấn đề trong vật lý.

1. Ví dụ 1: Ba điện tích \( q \) đặt tại ba đỉnh của một tam giác đều có cạnh \( a \). Tính lực tác dụng lên mỗi điện tích do hai điện tích còn lại gây ra.
• Giải: Để giải bài toán này, trước tiên ta tính lực tương tác giữa mỗi cặp điện tích bằng công thức: \[ F = k \cdot \frac{{q^2}}{{a^2}} \] Sau đó, tổng hợp các lực này để tìm lực tổng tác dụng lên mỗi điện tích.
2. Ví dụ 2: Tính cường độ điện trường tại tâm tam giác đều tạo bởi ba điện tích \( q \) giống hệt nhau.
• Giải: Do tính đối xứng, các cường độ điện trường do mỗi điện tích gây ra tại tâm sẽ triệt tiêu nhau, dẫn đến cường độ điện trường tổng hợp tại tâm bằng 0.
3. Bài tập 1: Ba điện tích \( q \) đặt tại các đỉnh của tam giác đều cạnh \( a \). Hãy tính công cần thiết để di chuyển một điện tích thứ tư \( q_4 \) từ vô cực đến tâm tam giác.
4. Bài tập 2: Ba điện tích \( q \) đặt tại ba đỉnh của tam giác vuông cân có cạnh góc vuông \( a \). Hãy tính lực tổng hợp tác dụng lên điện tích đặt tại đỉnh góc vuông còn lại.

Các ví dụ và bài tập này không chỉ giúp bạn nắm vững lý thuyết mà còn tạo điều kiện thực hành và kiểm tra kỹ năng giải toán, đảm bảo sự hiểu biết sâu sắc về tương tác giữa các điện tích trong các hệ khác nhau.

Bài toán ba điện tích q giống hệt nhau không chỉ là một bài toán lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tiễn quan trọng. Việc hiểu và áp dụng nguyên lý tương tác giữa các điện tích có thể hỗ trợ trong nhiều lĩnh vực như điện tử, thiết kế mạch, và công nghệ viễn thông.

1. Thiết kế mạch điện tử: Trong thiết kế các mạch điện tử, nguyên lý tương tác Coulomb được sử dụng để tính toán lực và điện trường giữa các thành phần điện tích. Điều này giúp đảm bảo mạch hoạt động ổn định và tránh hiện tượng quá tải điện áp.
2. Điều khiển hạt trong các thiết bị y tế: Nguyên lý của ba điện tích được áp dụng trong công nghệ điều khiển các hạt điện tích trong các thiết bị y tế, như máy chụp cộng hưởng từ (MRI). Các hạt mang điện được điều khiển và định hướng dựa trên tương tác Coulomb để tạo ra hình ảnh chi tiết của cơ thể.
3. Ứng dụng trong viễn thông: Trong viễn thông, tương tác giữa các điện tích đóng vai trò quan trọng trong việc phát triển và tối ưu hóa các thiết bị truyền tín hiệu, đảm bảo tín hiệu được truyền tải một cách hiệu quả và không bị nhiễu.
4. Nghiên cứu và phát triển vật liệu: Bài toán ba điện tích còn được sử dụng trong nghiên cứu các vật liệu mới có tính chất điện đặc biệt, hỗ trợ trong việc phát triển các thiết bị lưu trữ năng lượng như pin và tụ điện.

Các ứng dụng này chứng minh rằng nguyên lý cơ bản của tương tác giữa ba điện tích không chỉ dừng lại ở lý thuyết mà còn có ý nghĩa quan trọng trong việc giải quyết các vấn đề thực tiễn, đóng góp vào sự phát triển của nhiều lĩnh vực công nghệ hiện đại.

Việc thực hành và ôn tập bài toán ba điện tích q giống hệt nhau là rất quan trọng để hiểu rõ hơn về tương tác Coulomb và các nguyên lý liên quan. Dưới đây là một số bước thực hành giúp bạn củng cố kiến thức và áp dụng vào các bài tập thực tế.

1. Ôn tập lý thuyết: Trước tiên, hãy đảm bảo rằng bạn đã nắm vững các khái niệm cơ bản về lực Coulomb, điện trường và thế năng điện. Hãy xem lại các công thức cơ bản và các định luật liên quan đến điện tích.
2. Luyện tập giải bài toán: Hãy bắt đầu với các bài toán cơ bản về tính lực tương tác giữa hai điện tích trước khi chuyển sang các bài toán phức tạp hơn với ba điện tích. Sử dụng Mathjax để biểu diễn công thức và giải thích từng bước.
3. Thực hiện các bài tập tự kiểm tra: Tạo ra các bài toán mới với ba điện tích q giống hệt nhau ở các vị trí khác nhau, sau đó tự giải và kiểm tra lại kết quả. Việc này sẽ giúp bạn phát hiện ra các sai sót và cải thiện kỹ năng giải toán.
4. Tham khảo các bài giải mẫu: Xem lại các bài giải mẫu từ các nguồn tài liệu đáng tin cậy để so sánh với cách giải của mình. Điều này giúp bạn học hỏi các phương pháp giải khác nhau và áp dụng vào các bài toán tương tự.
5. Thảo luận nhóm: Tham gia vào các nhóm học tập để thảo luận và giải quyết các bài toán khó. Việc trao đổi với người khác sẽ giúp bạn mở rộng kiến thức và tìm ra các phương pháp giải mới.

Việc thực hành liên tục và áp dụng kiến thức vào các bài toán thực tế sẽ giúp bạn nắm vững chủ đề này, chuẩn bị tốt cho các kỳ thi và ứng dụng trong các lĩnh vực liên quan đến vật lý và kỹ thuật.

Để mở rộng kiến thức về bài toán ba điện tích q giống hệt nhau, bạn có thể tham khảo thêm các tài liệu và nguồn thông tin sau đây. Những tài liệu này không chỉ giúp bạn củng cố kiến thức lý thuyết mà còn cung cấp các ví dụ thực tế và bài tập đa dạng.

• Sách giáo khoa Vật lý: Tìm đọc các chương về điện trường và lực Coulomb trong sách giáo khoa Vật lý lớp 11. Đây là nguồn tài liệu cơ bản và đáng tin cậy giúp bạn hiểu rõ hơn về nguyên lý tương tác giữa các điện tích.
• Bài giảng trực tuyến: Tham gia các khóa học trực tuyến hoặc xem video bài giảng từ các giảng viên chuyên ngành Vật lý. Những bài giảng này thường cung cấp các ví dụ thực tế và bài tập minh họa để bạn thực hành.
• Bài viết trên các diễn đàn học thuật: Tham gia vào các diễn đàn học thuật hoặc cộng đồng học tập trực tuyến, nơi bạn có thể thảo luận và chia sẻ kinh nghiệm với những người cùng quan tâm đến chủ đề này.
• Bài báo khoa học: Đọc các bài báo khoa học hoặc các tạp chí chuyên ngành Vật lý để nắm bắt các nghiên cứu mới nhất về tương tác điện tích và các ứng dụng của chúng trong thực tế.
• Bài tập nâng cao: Thực hành các bài tập nâng cao từ các sách bài tập chuyên sâu hoặc các nguồn tài liệu trên mạng. Các bài tập này sẽ giúp bạn rèn luyện kỹ năng giải quyết các bài toán phức tạp.

Việc tham khảo thêm nhiều nguồn tài liệu sẽ giúp bạn nắm vững kiến thức, hiểu sâu hơn về bài toán ba điện tích q giống hệt nhau, và tự tin hơn trong việc áp dụng kiến thức này vào các bài tập và thực tế.