Bảng tổng hợp công thức lượng giác đầy đủ

Tỉ số lượng giác là một khái niệm quan trọng trong toán học, đặc biệt là trong lượng giác tam giác vuông. Trong bài viết này, chúng ta sẽ điểm qua các công thức lượng giác cơ bản và cách áp dụng chúng.

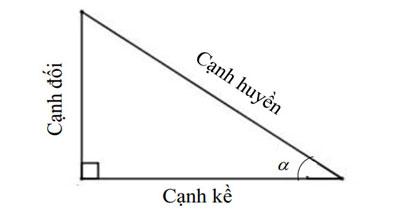
Khái niệm tỉ số lượng giác của góc nhọn

Trong một tam giác vuông, chúng ta sẽ có các tỉ số lượng giác cơ bản như sin, cos, tan, và cot. Các công thức này tính toán tỉ lệ giữa các cạnh của tam giác.

Các công thức lượng giác cơ bản

Các công thức lượng giác cơ bản như tanx = sinx / cosx và cotx = cosx / sinx giúp chúng ta tính toán các tỉ số giữa các cạnh trong tam giác vuông.

Các công thức cộng lượng giác

Công thức này giúp chúng ta tính toán tỉ số giữa các góc cộng hoặc trừ trong tam giác vuông. Ví dụ: sin(a ± b) = sin(a).cos(b) ± cos(a).sin(b). Để nhớ các công thức này, một câu thơ hữu ích là: “Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.”

Bạn đang xem: Bảng tổng hợp công thức lượng giác đầy đủ

Công thức các cung liên kết trên đường tròn lượng giác

Trong trường hợp các góc đối nhau, chúng ta có các công thức như cos(-x) = cos(x), sin(-x) = -sin(x), tan(-x) = -tan(x), cot(-x) = -cot(x). Tương tự, chúng ta cũng có các công thức cho các góc bù nhau và góc phụ nhau.

Công thức nhân lượng giác

Xem thêm : Số nguyên tố là gì? Ví dụ minh họa, tính chất, bảng số nguyên tố

Công thức lượng giác nhân đôi làm cho tính toán các tỉ số lượng giác trở nên dễ dàng hơn. Ví dụ, sin(2x) = 2sin(x).cos(x). Chúng ta có thể nhớ công thức này bằng câu thơ: “Sin gấp đôi bằng 2 sin cos.”

Công thức hạ bậc lượng giác

Công thức lượng giác hạ bậc được tạo ra bằng cách biến đổi các công thức lượng giác cơ bản. Điều này giúp chúng ta giải quyết các bài toán phức tạp hơn.

Công thức lượng giác biến tổng thành tích

Chúng ta cũng có công thức để biến đổi tổng các tỉ số lượng giác thành tích. Điều này đặc biệt hữu ích trong việc giải quyết các bài tập phức tạp về lượng giác.

Công thức nghiệm của phương trình lượng giác

Xem thêm : Tổ tiên dặn kỹ: Cây dâu trước nhà đang giàu mấy cũng lụi bại nhưng chuyển đúng chỗ này thì như có vàng mười

Công thức nghiệm của phương trình lượng giác giúp chúng ta tìm các giá trị của lượng giác tương ứng với một góc hoặc một tỉ số lượng giác.

Bảng xét dấu và giá trị lượng giác

Chúng ta có thể sử dụng bảng xét dấu và giá trị lượng giác để xác định dấu và giá trị của các tỉ số lượng giác ứng với các góc trong các phần tư số khác nhau.

Bảng giá trị lượng giác của các góc đặc biệt

Cuối cùng, chúng ta có một bảng giá trị lượng giác của các góc đặc biệt như 0, 30, 45, 60 và 90 độ. Bảng này giúp chúng ta nắm vững các giá trị lượng giác trong việc giải quyết các bài toán lượng giác.

Trên đây là những kiến thức cơ bản về công thức lượng giác mà chúng ta cần biết. Hy vọng rằng bài viết này đã giúp các bạn nắm vững và sử dụng hiệu quả các công thức này trong việc giải quyết các bài toán liên quan. Đừng ngần ngại đăng ký tài khoản tại VUIHOC để có thêm tài liệu ôn tập và xây dựng lộ trình ôn thi Toán THPT sớm nhé.

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập