Vị trí vân tối trong thí nghiệm giao thoa: Khám phá chi tiết và ứng dụng thực tế

Thí nghiệm giao thoa ánh sáng là một trong những thí nghiệm quan trọng trong lĩnh vực quang học, được thực hiện lần đầu bởi Thomas Young. Trong thí nghiệm này, hai sóng ánh sáng từ hai nguồn kết hợp sẽ giao thoa với nhau, tạo ra các vân sáng và vân tối trên màn quan sát.

1. Cách xác định vị trí vân tối

Vị trí của các vân tối trong thí nghiệm giao thoa có thể được xác định dựa trên công thức:

\[
x = \left(k + \dfrac{1}{2}\right) \dfrac{\lambda D}{a}
\]

• \(x\): Vị trí của vân tối
• \(k\): Thứ tự của vân tối (k = 0, ±1, ±2,...)
• \(\lambda\): Bước sóng ánh sáng sử dụng trong thí nghiệm
• \(D\): Khoảng cách từ hai khe đến màn quan sát
• \(a\): Khoảng cách giữa hai khe

2. Nguyên lý hoạt động của thí nghiệm

Thí nghiệm Young hoạt động dựa trên nguyên lý giao thoa của ánh sáng. Khi hai chùm sóng từ hai khe giao thoa với nhau, chúng có thể cộng hưởng để tạo ra các vân sáng (cực đại) hoặc triệt tiêu nhau tạo ra các vân tối (cực tiểu). Các vân sáng và vân tối này xuất hiện luân phiên nhau trên màn quan sát.

3. Ứng dụng của vị trí vân tối

• Quang học: Vị trí vân tối được sử dụng để hiệu chuẩn các thiết bị quang học như kính hiển vi và máy quét hình ảnh.
• Y học: Sử dụng để đo kích thước các tế bào và cấu trúc siêu nhỏ trong các mẫu mô sinh học.
• Công nghệ laser: Ứng dụng trong việc kiểm tra và điều chỉnh độ chính xác của các hệ thống laser.

4. Các yếu tố ảnh hưởng đến vị trí vân tối

Vị trí vân tối trong thí nghiệm giao thoa phụ thuộc vào nhiều yếu tố:

• Bước sóng ánh sáng (\(\lambda\)): Bước sóng càng lớn, khoảng cách giữa các vân càng lớn.
• Khoảng cách giữa hai khe (\(a\)): Khoảng cách này càng nhỏ, các vân sáng và vân tối càng cách xa nhau.
• Khoảng cách từ khe đến màn (\(D\)): Khoảng cách càng lớn, các vân càng cách xa nhau.

5. Công thức tính khoảng vân

Khoảng vân (\(i\)) là khoảng cách giữa hai vân sáng liên tiếp hoặc hai vân tối liên tiếp, được tính bằng công thức:

\[
i = \dfrac{\lambda D}{a}
\]

Trong đó:

• \(i\): Khoảng vân
• \(\lambda\): Bước sóng của ánh sáng

6. Kết luận

Thí nghiệm giao thoa ánh sáng không chỉ giúp hiểu rõ hơn về tính chất sóng của ánh sáng mà còn có nhiều ứng dụng thực tế trong các lĩnh vực quang học, y học, và công nghệ. Việc xác định chính xác vị trí của các vân tối giúp các nhà khoa học và kỹ sư có thể áp dụng các nguyên lý quang học vào thiết kế và kiểm tra các thiết bị công nghệ cao.

Thí nghiệm giao thoa ánh sáng là một trong những thí nghiệm kinh điển trong lĩnh vực quang học, lần đầu tiên được thực hiện bởi nhà vật lý Thomas Young vào năm 1801. Thí nghiệm này đã góp phần quan trọng trong việc chứng minh bản chất sóng của ánh sáng, một trong những phát hiện vĩ đại nhất trong lịch sử vật lý.

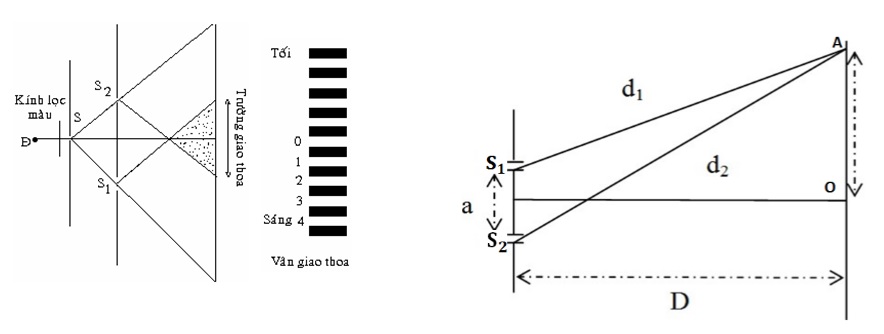
Thí nghiệm giao thoa được thực hiện bằng cách chiếu một chùm ánh sáng đơn sắc qua hai khe hẹp song song rất gần nhau. Các sóng ánh sáng từ hai khe này giao thoa với nhau, tạo ra một hệ thống các vân sáng và vân tối trên màn quan sát. Hiện tượng này là kết quả của sự giao thoa giữa các sóng ánh sáng, khi hai sóng gặp nhau chúng có thể tăng cường hoặc triệt tiêu lẫn nhau tùy thuộc vào sự lệch pha.

• Bước sóng ánh sáng: Ánh sáng sử dụng trong thí nghiệm thường là ánh sáng đơn sắc với bước sóng \(\lambda\) cố định, để các kết quả thu được có tính đồng nhất.
• Khe Young: Hai khe hẹp này đóng vai trò là hai nguồn sáng kết hợp, phát ra hai sóng ánh sáng có cùng pha ban đầu.
• Màn quan sát: Là nơi thu nhận hình ảnh giao thoa của các vân sáng và vân tối, cho thấy sự tương tác giữa các sóng ánh sáng.

Thí nghiệm giao thoa ánh sáng của Young đã mở đường cho nhiều nghiên cứu khác trong quang học và đã được ứng dụng rộng rãi trong các lĩnh vực khác nhau của khoa học và công nghệ. Đây cũng là một thí nghiệm quan trọng trong việc khẳng định lý thuyết sóng của ánh sáng, đối lập với quan điểm cổ điển về bản chất hạt của ánh sáng.

Trong thí nghiệm giao thoa ánh sáng, vị trí của các vân tối trên màn quan sát được xác định dựa trên sự giao thoa của các sóng ánh sáng từ hai khe hẹp. Khi hai sóng ánh sáng giao thoa và triệt tiêu lẫn nhau, chúng tạo ra các vân tối, là những vị trí có cường độ ánh sáng thấp nhất.

Công thức xác định vị trí của các vân tối được biểu diễn như sau:

\[
x = \left(k + \dfrac{1}{2}\right) \dfrac{\lambda D}{a}
\]

• \(x\): Vị trí của vân tối tính từ vị trí trung tâm (vân sáng trung tâm).
• \(k\): Thứ tự của vân tối (k = 0, ±1, ±2,...).
• \(\lambda\): Bước sóng của ánh sáng sử dụng trong thí nghiệm.
• \(D\): Khoảng cách từ hai khe đến màn quan sát.
• \(a\): Khoảng cách giữa hai khe hẹp.

Công thức trên cho thấy rằng vị trí của vân tối phụ thuộc vào bước sóng ánh sáng, khoảng cách giữa các khe và khoảng cách từ khe đến màn. Khi các yếu tố này thay đổi, vị trí các vân tối trên màn cũng sẽ thay đổi tương ứng. Điều này giúp các nhà khoa học có thể kiểm soát và dự đoán chính xác vị trí các vân trong các thí nghiệm quang học.

Hiện tượng giao thoa ánh sáng là minh chứng rõ ràng cho tính chất sóng của ánh sáng, trong đó các sóng ánh sáng từ các nguồn kết hợp giao thoa với nhau tạo ra các vân sáng và vân tối trên màn quan sát. Sự xuất hiện của các vân sáng và vân tối không chỉ phụ thuộc vào bước sóng của ánh sáng mà còn vào các yếu tố như khoảng cách giữa hai khe sáng và khoảng cách từ khe đến màn.

3.1 Phân tích vai trò của bước sóng

Bước sóng ánh sáng (\(\lambda\)) đóng vai trò quan trọng trong việc xác định vị trí các vân giao thoa. Vị trí của các vân sáng và vân tối trên màn quan sát được xác định bởi công thức:

\[
x_k = \left(k + \frac{1}{2}\right) \frac{\lambda D}{d}
\]

Trong đó:

• \(x_k\) là vị trí của vân tối thứ \(k\).
• \(D\) là khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát.
• \(d\) là khoảng cách giữa hai khe giao thoa.
• \(k\) là bậc của vân tối (k = 0, 1, 2,...).

Bước sóng càng lớn thì khoảng cách giữa các vân giao thoa càng lớn, dẫn đến việc các vân tối sẽ cách xa nhau hơn.

3.2 Ảnh hưởng của khoảng cách giữa hai khe

Khoảng cách giữa hai khe \(d\) có ảnh hưởng trực tiếp đến khoảng vân giao thoa. Công thức tính khoảng vân \(i\) là:

\[
i = \frac{\lambda D}{d}
\]

Nếu khoảng cách \(d\) càng lớn, khoảng vân sẽ càng nhỏ, dẫn đến các vân tối gần nhau hơn. Ngược lại, nếu \(d\) nhỏ thì các vân tối sẽ cách xa nhau.

3.3 Tác động của khoảng cách từ khe đến màn

Khoảng cách từ khe đến màn \(D\) cũng ảnh hưởng đáng kể đến vị trí và khoảng cách giữa các vân giao thoa. Khi \(D\) tăng lên, các vân giao thoa, bao gồm cả vân tối, sẽ xuất hiện xa nhau hơn. Điều này có nghĩa là với cùng một bước sóng và khoảng cách giữa các khe, việc thay đổi khoảng cách từ khe đến màn có thể thay đổi rõ rệt hình ảnh giao thoa quan sát được trên màn.

Như vậy, hiện tượng giao thoa ánh sáng không chỉ giúp chứng minh tính chất sóng của ánh sáng mà còn cung cấp công cụ để đo lường các đặc tính vật lý như bước sóng, độ đồng nhất của ánh sáng, và tính chính xác trong việc chế tạo các thiết bị quang học.

Vị trí vân tối trong thí nghiệm giao thoa ánh sáng không chỉ là một khái niệm quan trọng trong lĩnh vực vật lý mà còn có nhiều ứng dụng thực tiễn trong các ngành khoa học và công nghệ khác nhau. Dưới đây là một số ứng dụng nổi bật:

4.1 Ứng dụng trong quang học

Trong quang học, sự xác định chính xác vị trí vân tối giúp cải thiện chất lượng của các thiết bị quang học như kính hiển vi, kính thiên văn và các hệ thống quang học phức tạp. Việc điều chỉnh khoảng cách giữa các khe hoặc các yếu tố khác có thể tối ưu hóa độ phân giải và khả năng quan sát chi tiết của các thiết bị này.

4.2 Ứng dụng trong y học

Vị trí vân tối cũng đóng vai trò quan trọng trong các phương pháp chẩn đoán y học hiện đại. Một trong những ứng dụng nổi bật là trong công nghệ chụp cắt lớp quang học (Optical Coherence Tomography - OCT), nơi sự giao thoa ánh sáng được sử dụng để tạo ra hình ảnh chi tiết của các mô bên trong cơ thể, giúp bác sĩ chẩn đoán bệnh lý một cách chính xác.

4.3 Ứng dụng trong công nghệ laser

Trong công nghệ laser, việc kiểm soát và điều chỉnh vị trí vân tối giúp tối ưu hóa các hệ thống laser, từ đó cải thiện hiệu suất phát xạ và sự ổn định của chùm tia laser. Điều này đặc biệt quan trọng trong các ứng dụng yêu cầu độ chính xác cao như gia công vật liệu bằng laser, in 3D, và truyền thông quang học.

Nhờ vào sự nghiên cứu sâu rộng về vị trí vân tối, các nhà khoa học và kỹ sư có thể ứng dụng hiệu quả các nguyên lý giao thoa ánh sáng để cải tiến và phát triển các công nghệ tiên tiến trong nhiều lĩnh vực khác nhau.

5.1 Bài toán tìm vị trí vân tối

Để xác định vị trí vân tối trong thí nghiệm giao thoa ánh sáng, chúng ta sử dụng công thức:

\[
x_k = \left(k + \frac{1}{2}\right) \frac{\lambda D}{a}
\]

Trong đó:

• \(x_k\) là vị trí của vân tối thứ \(k\) (tính từ vân trung tâm).
• \(k\) là số thứ tự của vân tối.
• \(\lambda\) là bước sóng của ánh sáng.
• \(D\) là khoảng cách từ hai khe đến màn quan sát.
• \(a\) là khoảng cách giữa hai khe.

Vân tối sẽ xuất hiện tại các vị trí mà hiệu đường đi của hai sóng từ hai khe đến điểm đó bằng một nửa bước sóng, một bước sóng rưỡi, hoặc nói cách khác là các giá trị lẻ của một nửa bước sóng.

5.2 Bài toán về khoảng vân

Khoảng vân \(i\) là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp nhau và được xác định bằng công thức:

\[
i = \frac{\lambda D}{a}
\]

Khi biết khoảng vân, ta có thể xác định vị trí của các vân sáng và vân tối trên màn. Khoảng vân cũng phụ thuộc vào bước sóng của ánh sáng sử dụng, khoảng cách giữa các khe và khoảng cách từ khe đến màn.

5.3 Bài toán về số vân sáng và vân tối

Số lượng vân sáng và vân tối xuất hiện trên màn có thể được tính toán dựa trên tổng chiều dài của màn và khoảng vân. Để tìm số lượng vân tối trong một khoảng xác định, ta cần xác định số thứ tự \(k\) tối đa có thể tồn tại trong khoảng đó:

\[
k_{\text{max}} = \frac{aL}{2\lambda D}
\]

Trong đó \(L\) là chiều dài của vùng giao thoa trên màn. Công thức này cho phép ước lượng tổng số vân tối có thể quan sát được trong một thí nghiệm cụ thể.

Các bài toán liên quan đến thí nghiệm giao thoa không chỉ giúp hiểu sâu hơn về bản chất sóng của ánh sáng mà còn có ứng dụng quan trọng trong các lĩnh vực như đo lường chính xác bước sóng ánh sáng hay thiết kế các thiết bị quang học.